作业7 投资问题

1.     问题

给定m单位钱，n项投资，并设函数f_i(x)表示将x元钱投入第i项投资所产生的效益，I = 1,2,…,n.问：如何分配这m元钱，使得投资的总效益最高。

2.     解析

主要使用动态规划的方法来对问题进行解决。

引入一个新的函数F_k(x)表示使用x单位钱投给前k个项目的最大效益，k = 1,2,…,n.由此可以得出递推方程

F_k(x) = max{f_k(x_k)+F_k-1(x-x_k)} 其中 0 <= x_k <= x,k = 1,2,…,n.

F₁(x) = f₁(x),F_k(0) = 0,k = 1,2,…,n.

       在这之中，fk是已知的量，因此对于F_k来说，我们只要知道F_k-1，就可以非常简单的进行计算。所以算法的大致思想就是从只有一个项目开始计算，一次向上计算。最终得到n个项目的最大效益

3.     设计

Typedef struct point{

       Int F;

       Int x;

}point;

Int invest[10][10]; //用来存储单个投资的效益f的映射关系。其中每行代表了一个投资的效益f的映射关系

Point F[10][10];//用来保存引入的新的映射，[m][n]上的point结构体数据中，使用F来表示，给定m单位的钱，使用前n项投资所获得的最大效益，使用x表示，在达成上述的最大效益时，第n项投资所投入的钱。

Int main()

{

       获取m和n，并得到投资的映射invest

       For(int k = 0;k < n;k++)

              For(int x = 1;x <= m;x++)

              Int maxi = 0;

              Int tmp = 0;

                     For(int xi = 0;xi <= x;xi++)

                            If(invest[k][xi] + F[k-1][x-xi].F > maxi)

                                   Maxi = invest[k][xi] + F[k-1][x-xi]

                                   Tmp = xi;

                           

                     F[k][x].F = maxi;

}

4.     分析

整个算法的主体部分主要是一个三重循环，对于最内存的循环，取值为[0,x]总共执行了x+1次的加法，x次的比较，由此可以得出一个求和的式子

对于加法的时间复杂度为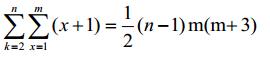 

比较的时间复杂度为

5.     源码

https://github.com/fanchile/Algorithm