大致题意:
- 有一个A字符串和一个B字符串,
- 操作将A或A的一个后缀修改为B,
- 求最少的操作数。
- 有三个操作为:
- 删除: 删除掉 A 中的某一个字符。
- 添加: 将某一个字符添加到 A 中任意位置。
- 替换: 将 A 中某一字符替换为另一个。
基本思路:
-
我最不擅长的的就是dp,然后这题就是dp。。。/kk
-
我看到dp就发怵啊,虽说
一腔热血在胸膛想了又想,但还是避免不了wa的遭遇。 -
然后看了一位大佬的博客戳我,我丢,居然这么简单。
-
(虽说他视频讲了一次,但我感觉他的文字比他讲的好多了 -
咳咳,不说废话了。
-
以f[i][j]表示将A的前i为操作为B的前j位的最少操作数。
-
然后就找方程啦。就有三个方式来推出f[i][j]。
-
第一个方式:
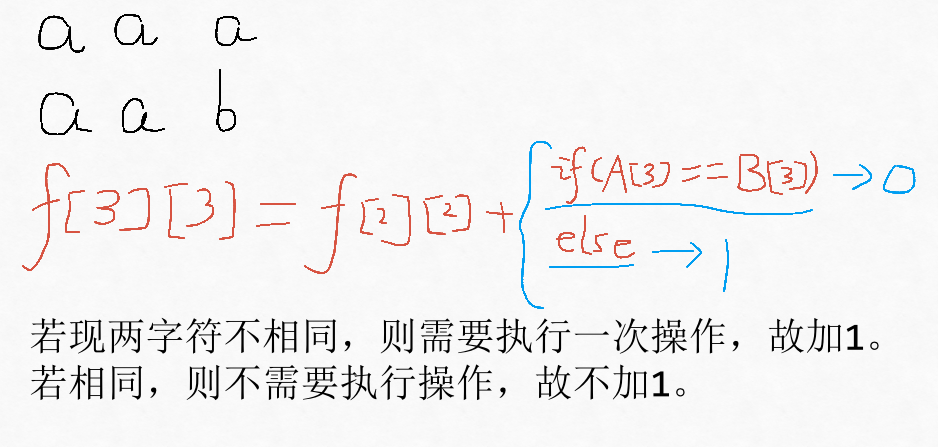
-
第二个方式:

-
第三个方式:

-
三个方式都好了,取最小的一个就是f[i][j]的答案了呢。
-
然后最后的答案就是f[ A的长度 ][ B的长度 ]。
Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <list>
using namespace std;
#define R read()
#define GC getchar()
#define ll long long
#define ull unsigned long long
#define INF 0x7fffffff
#define LLINF 0x7fffffffffffffff
ll read(){
ll s=0,f=1;
char c=GC;
while(c<'0'||c>'9'){if(c=='-')f=-f;c=GC;}
while(c>='0'&&c<='9'){s=s*10+c-'0';c=GC;}
return s*f;
}
char a[1010],b[1010];
int aLen,bLen;
int f[1010][1010];
int main(){
cin>>a+1>>b+1;//"黑科技",下标以1开始,但是有些字符串的东西就不能用了
aLen=strlen(a+1);
bLen=strlen(b+1);
for(int i=1;i<=aLen;++i){//初始化
f[i][0]=0;
}
for(int i=1;i<=bLen;++i){
f[0][i]=i;
}
for(int i=1;i<=aLen;++i){
for(int j=1;j<=bLen;++j){
f[i][j]=min(f[i-1][j-1]+(!(a[i]==b[j])),min(f[i-1][j]+1,f[i][j-1]+1));
//递推公式
}
}
printf("%d",f[aLen][bLen]);//输出
return 0;
}