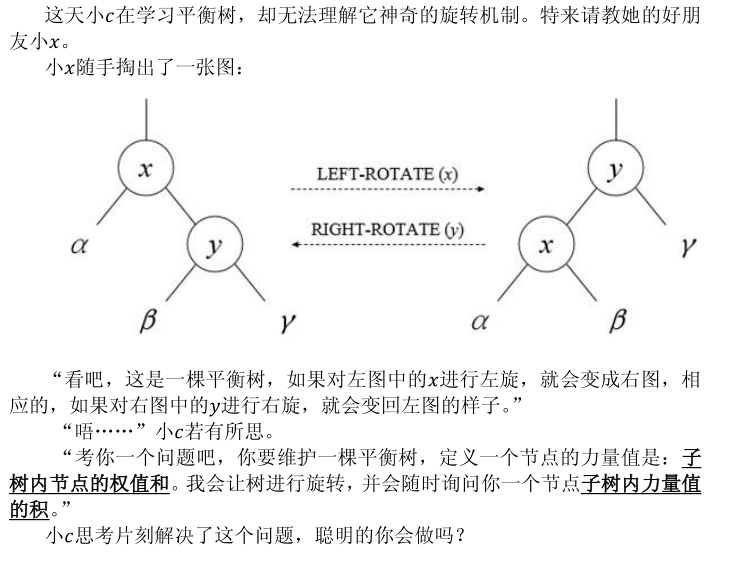
平衡树的问题,很容易想到中序遍历
那么我们给每一个节点记录一下中序遍历中它子树所在的区间,一次旋转显然只会改变两个节点的值
对于询问我们用线段树区间求积就可以了
#pragma GCC optimize("O3")
#pragma G++ optimize("O3")
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define N 200010
#define M 1000000007
#define LL long long
#define mid (l+r>>1)
#define ls l,mid,x<<1
#define rs mid+1,r,x<<1|1
using namespace std;
int clk,n,m,l[N],r[N],v[N];
int w[N],wl[N],wr[N],p[N],s[N],rk[N],rt;
int T[N<<2];
inline void ps(int x){
s[x]=(s[l[x]]+s[r[x]]+v[x])%M;
wl[x]=(l[x]?wl[l[x]]:rk[x]);
wr[x]=(r[x]?wr[r[x]]:rk[x]);
}
inline void dfs(int x){
if(l[x]) dfs(l[x]);
w[++clk]=x; rk[x]=clk;
if(r[x]) dfs(r[x]);
ps(x);
}
inline void build(int l,int r,int x){
if(l==r){ T[x]=s[w[l]]; return; }
build(ls);
build(rs);
T[x]=((LL)T[x<<1]*T[x<<1|1])%M;
}
inline void update(int l,int r,int x,int p,int k){
if(l==r){ T[x]=k; return; }
if(p<=mid) update(ls,p,k); else update(rs,p,k);
T[x]=((LL)T[x<<1]*T[x<<1|1])%M;
}
inline LL query(int l,int r,int x,int L,int R){
if(L<=l && r<=R) return T[x];
LL ans=1;
if(L<=mid) ans=ans*query(ls,L,R)%M;
if(mid<R) ans=ans*query(rs,L,R)%M;
return ans;
}
int main(){
freopen("splay.in","r",stdin);
freopen("splay.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i){
scanf("%d%d%d",v+i,l+i,r+i);
p[l[i]]=i; p[r[i]]=i;
}
for(int i=1;i<=n;++i) if(!p[i]) rt=i;
dfs(rt);
build(1,n,1);
for(int o,x,y;m--;){
scanf("%d%d",&o,&x);
if(o==2) printf("%lld
",query(1,n,1,wl[x],wr[x]));
else{
if(!o&&l[x]){
y=l[x]; o=p[x];
l[x]=r[y]; r[y]=x;
if(l[x]) p[l[x]]=x; p[x]=y; p[y]=o;
if(o){
if(l[o]==x) l[o]=y; else r[o]=y;
} else rt=y;
ps(x); ps(y);
update(1,n,1,rk[x],s[x]);
update(1,n,1,rk[y],s[y]);
} else if(o&&r[x]){
y=r[x]; o=p[x];
r[x]=l[y]; l[y]=x;
if(r[x]) p[r[x]]=x; p[x]=y; p[y]=o;
if(o){
if(l[o]==x) l[o]=y; else r[o]=y;
} else rt=y;
ps(x); ps(y);
update(1,n,1,rk[x],s[x]);
update(1,n,1,rk[y],s[y]);
}
}
}
}