【动态规划】背包问题-例题分析

多重背包问题的变式

装备强化

题目描述
网游中，装备强化是提升角色战力的常见方法。 现在你参与开发的游戏中也有这项功能，团队正在设计每件装备强化所能提升的战力及需要消耗的金币数。为了设计出一个合理的强化系统，决定先做一些强化模拟测试，而你现在就在是该模拟程序的开发者。 假设现在有n件可以同时穿戴的装备，对于第i件装备，最多可以强化mi 次，对于第i件装备的第j次强化，会增加fij 的战力，并需要消耗gij 个金币。现在给出所有装备的数据，以及初始拥有的金币数量，求最多可以增加多少战力。
输入描述:
输入文件的第一行为一个正整数T，表示测试数据组数。
接下来有T组数据。每组数据第1行为两个整数n和s，分别表示装备数量及初始拥有的金币数量。接下来是n行，每行表示一个装备，其中每行第一项为一个字符串，表示装备的名称，第二项为非负整数mi，表示装备最多可强化的次数，接下来为2*mi个非负整数，表示每次强化会增加的战力及消耗的金币数。

数据范围：
对于所有数据文件，1<=T<=10。装备的名称最大长度不超过32个字符，由大小写字母或数字组成。每件装备最多强化次数mi满足0<=mi<=3。所有战力数值和金币数为非负整数且不超过10,000,000。
对于其中的20%数据，满足装备数1<=n<=5；
另外有30%数据，满足装备数1<=n<=10；
另外有30%数据，满足装备数1<=n<=16；
最后剩下的20%数据，满足装备数1<=n<=20。

数据保证只有唯一的强化方案能达到最大战力。

输出描述:
对于每个测试数据，第一行为一个整数，表示最多可提升的战力。接下来是n行，表示达到这个战力时每件装备分别的强化次数，形式为“装备名称+强化次数”。输出装备的顺序要与输入数据一致。更详细的格式请参照输出样例。

输入例子:
3
4 100
Helm 1 20 30
Gloves 1 30 40
Boots 1 10 10
Sword 1 50 50
5 10
Item1 0
Item2 1 10000 100
Item3 1 10 10
Item4 3 1 0 2 1 3 2
Item5 3 0 4 1 1 5 1
6 256
1x 2 12 43 35 58
2x 2 34 54 88 31
3x 2 43 10 15 55
4x 2 32 54 19 19
5x 2 84 1 15 45
6x 2 19 40 99 12

输出例子:
90
Helm+0
Gloves+1
Boots+1
Sword+1
12
Item1+0
Item2+0
Item3+0
Item4+3
Item5+3
418
1x+0
2x+2
3x+1
4x+2
5x+1
6x+2

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;

//dp方程
const int max_n = 20 + 5;
const int max_s = 100 + 10;
struct Equipment {
	string name;
	int mi;
	vector<int> fij; //战力
	vector<int> gij; //金币
};

int main()
{
	int T;
	cin >> T;
	for (int c = 0; c < T; c++)
	{
		int n, s;
		cin >> n >> s;

		vector<Equipment> items(n+1); //n个装备

                //注意这里用的是i=1，因为我们希望i就代表第i个装备，0用来初始化dp中的0位置

		for (int i = 1; i <= n; i++)
		{
			cin >> items[i].name >> items[i].mi;
			for (int j = 0; j < items[i].mi; j++)
			{
				int fij, gij;
				cin >> fij >> gij;
				items[i].fij.push_back(fij);
				items[i].gij.push_back(gij);
			}
		}

		//输入完成

		int dp[max_n][max_s] = { 0 };
		int result[max_n][3] = { 0 };
                  
		for (int i = 1; i <= n; i++) //每个装备，注意这里也是i=1,i<=n
		{
			for (int j = s; j > 0; j--)
			{
				for (int k = 0; k < items[i].mi; k++)
				{
                                        int k_f = 0;//升级K次得到的战力
					int k_g = 0; //升级K次用掉的金币					

					for (int n = 0; n <= k; n++)
					{
						k_f += items[i].fij[n];
						k_g += items[i].gij[n];
					}

					if (j - k_g >= 0)
					{
                                               dp[i][j] = max(dp[i][j], dp[i - 1][j - k_g] + k_f);
					}
				}
			}
		}
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j < s; j++)
			{
				cout << dp[i][j]<<"  ";
			}
			cout << dp[i][s]<<endl;
		}
	}
}

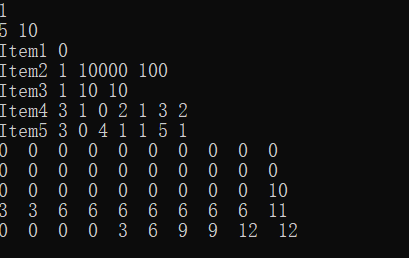
在这个dp里面，有一个问题需要解决，就是如何输出该升级了那些（选择了那些物品，这个问题暂缓）
-----------------施工中---------------------