一、栈
1. 栈的基本概念
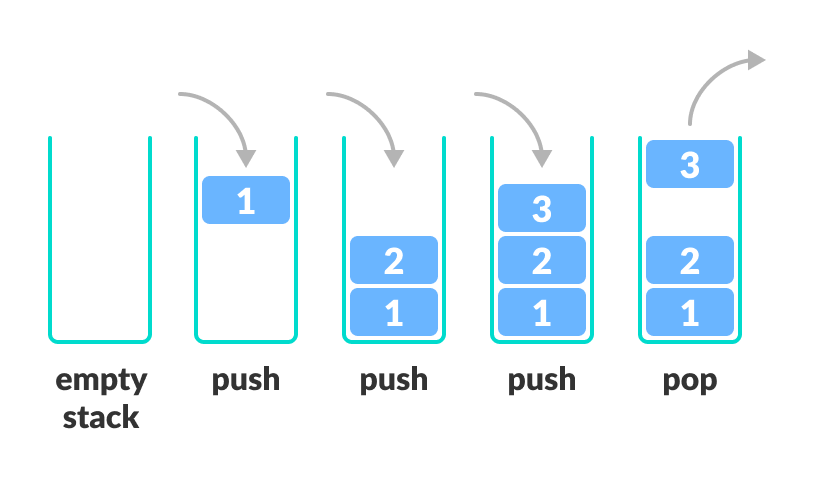
- 栈(Stack):是限定仅在一端(栈顶)进行插入或者删除操作的线性表,是一种后进先出的线性表
- 栈顶(Top):允许进行插入或删除操作的一端
- 栈底(Bottom):固定的,不允许进行任何操作的一端
2.栈的存储结构
顺序存储(数组实现)
在JDK中,Java Stack类是vector的一个子类,继承vector,在util包下。并且只定义了默认构造方法,大部分方法的实现也来源于vector。
public class Stack<E> extends Vector<E> {}
代码实现
public class ArrayStack{
private static final int DEFAULT_CAPACITY = 100; //栈的默认容量
private Object[] arrStack; //实现栈的数组
private int topOfStack; //栈顶
//栈的初始化
public ArrayStack(){
arrStack = new Object[DEFAULT_CAPACITY];
topOfStack = -1;
}
//栈空判断
public boolean isEmpty(){
return topOfStack == -1;
}
//栈满判断
public boolean isFull(){
return topOfStack == DEFULT_CAPACITY - 1;
}
//入栈
public void push(Object o){
if(isFull()){
throw new RuntimeException("栈满");
}
arrStack[topOfStack++] = o;
}
//出栈
public Object pop(){
if(isEmpty()){
throw new RuntimeException("栈空");
}
return arrStack[topOfStack--];
}
}
3.栈的应用
- 表达式转换和求值
- 括号匹配
- 递归程序的非递归化
- 二叉树遍历
- 图的深度优先搜寻
二、队列
1.队列的基本概念
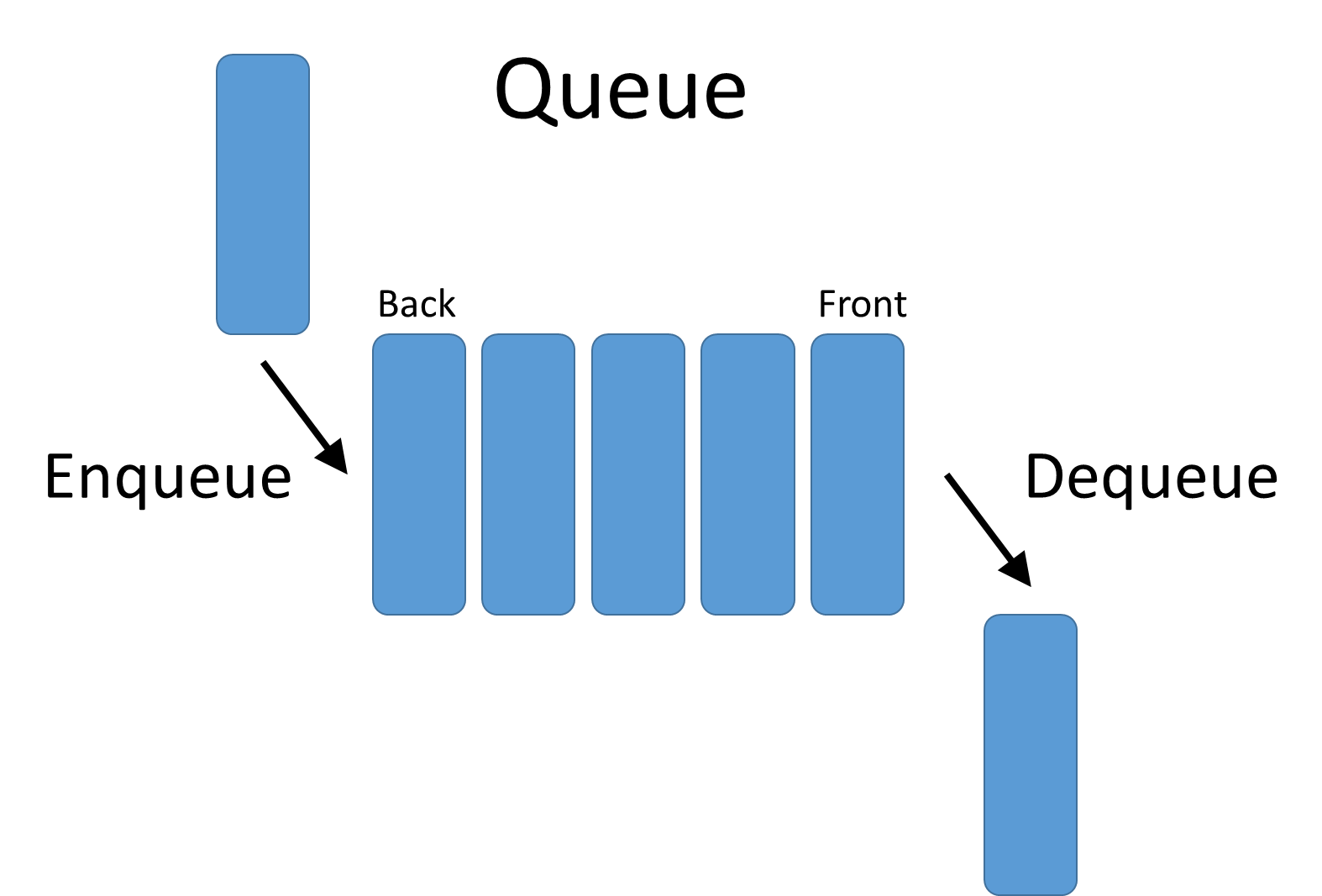
- 队列(Queue):限定在一端进行插入,另一端进行删除。是一种先进先出的线性表
- 队头:允许删除的一端
- 队尾:允许插入的一端
2. 队列的存储结构
在JDK中,队列是collection的一个子类
2.1 顺序队列(数组实现)
设front指向队头元素,rear指向队尾元素,那么
队空条件:front = rear = -1;
入队操作:队不满时,队尾rear指针向后移一位,再将值放入队尾,即++rear;
出队操作:队非空时,队头指针向后移动一位,再从队头取值,即++front;
代码实现
class ArrayQueue{
private Object[] arrQueue;
private int front;
private int rear;
private int maxSize;
//构造函数初始化
public ArrayQueue(){
arrQueue = new Object[maxSize];
front = -1;
rear = -1;
}
//判断队列是否已满
public boolean isFull(){
return rear == this.maxSize - 1;
}
//判断队列是否为空
public boolean isEmpty(){
return rear == front;
}
//入队
public void EnQueue(Object o){
if(isFull()){
throw new RuntimeException("队列已满");
}
arrQueue[++rear] = o;
}
//出队
public Object DeQueue(){
if(isEmpty()){
throw new RuntimeException("队列为空");
}
return arrQueue[++front];
}
}
2.2 循环队列(数组实现)
在上面的顺序队列中,能否通过rear == maxSize - 1 来判断数组中元素是否已满?答案是不能,如图,此时已经不能再插入新的元素,然而在数组左侧仍然有空位,这就是顺序队列中的假溢出
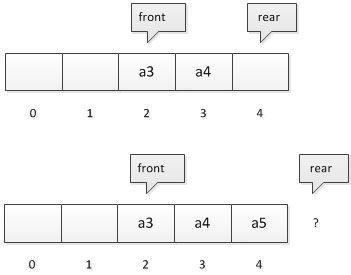
因此,就引出了循环队列,将存储队列元素的数组表从逻辑上看成一个环,当队头front = maxSize -1后,再前进一格位置就到达数组的0位,节约了内存空间。
队空条件:front = rear;
队满条件:(rear + 1) % maxSize == front;
入队操作:rear = (rear + 1) % maxSize;
出队操作:front = (front + 1) % maxSize;
队列长度:(rear + maxsize - front) % maxSize;
代码实现
class CircleQueue{
private Object[] arrQueue;
private int front;
private int rear;
private int maxSize;
//构造函数初始化
public CircleQueue(){
arrQueue = new Object[maxSize];
front = 0;
rear = 0;
}
//判断队列是否已满
public boolean isFull(){
return (rear + 1) % maxSize == front;
}
//判断队列是否为空
public boolean isEmpty(){
return rear == front;
}
//入队
public void EnQueue(Object o){
if(isFull()){
throw new RuntimeException("队列已满");
}
arrQueue[rear] = o;
rear = (rear + 1) % maxSize;
}
//出队
public Object DeQueue(){
if(isEmpty()){
throw new RuntimeException("队列为空");
}
Object value = arrQueue[front];
front = (front + 1) % maxSize;
return value;
}
//队列长度
public int len(){
if(isEmpty()){
return 0;
}
return (rear + maxSize - front ) % maxSize;
}
}
3. 队列的应用
- 作业排队
- 层序遍历二叉树