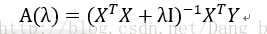一、经验、期望和结构风险
1.总结:
经验风险是局部的,基于训练集所有样本点损失函数最小化的;期望风险是全局的,是基于所有样本点的损失函数最小化的。
经验风险函数是现实的,可求的;期望风险函数是理想化的,不可求的。
结构风险是对经验风险和期望风险的折中。
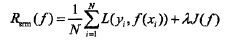
2.参考:
https://blog.csdn.net/liyajuan521/article/details/44565269
二、岭回归
1.总结:
是对最小二乘拟合的一种改进,原本最小二乘拟合的最优解为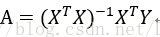
加上正则项变成: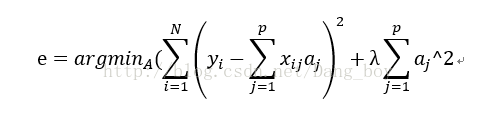
2.参考:
https://blog.csdn.net/dang_boy/article/details/78504258
三、kmeans
1.流程:

2.缺点:
可能局部最优;K需要给定;对初始聚类中心敏感;
3.改进:
(1)kmeans++:(解决聚类中心随机选择)
第一个聚类中心随机选择,第n+1个选距前面的最远的点最为下一个聚类中心。
(2)ISODATA:(解决K无法估计)
当属于某个类别的样本数过少时把这个类别去除,当属于某个类别的样本数过多、分散程度较大时把这个类别分为两个子类别。
(3)核化kmeans:(解决原始数据不在一个空间)
4.参考:
https://www.cnblogs.com/yixuan-xu/p/6272208.html
四、Knn
1.思想:
对测试样本,选择训练样本中与其最相似的k个样本中最多的标签,作为自己的预测类别。
2.优缺点:
对异常值不敏感;
复杂度高;
3.K的选择:
k太小容易过拟合;k太大容易判别错误;k一般选择一个较小的值,然后交叉验证最优k值。
4.参考:
https://www.cnblogs.com/yushuo1990/p/5879341.html
五、最优化方法
1.梯度下降法:
(1)思想:
用当前位置负梯度方向作为搜索方向,因为该方向为当前位置的最快下降方向,所以也被称为是”最速下降法“。最速下降法越接近目标值,步长越小,前进越慢。
(2)改进:
随机梯度下降:每次更新使用训练集的一个样本。速度快,准确度下降。
批量梯度下降:每迭代一次都用到训练集所有的数据。全局最优,速度慢。
2.牛顿法:
(1)思想:
是一种求解无约束问题最优化的方法,基于当前位置的切线来确定下一次的位置。
(2)方法:
目的:求解min f(x)
过程:将f(x)在xk处进行二阶泰勒展开,并对x进行求导,令导数=0得到:
结果: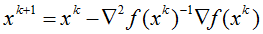
(3)优缺点:
二阶收敛,速度快;要计算一阶和二阶偏导,计算量大。
(4)对比:

3.拟牛顿法:
(1)思想:
改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷,它使用正定矩阵来近似Hessian矩阵的逆,从而简化了运算的复杂度。
(2)参考:
https://www.cnblogs.com/richqian/p/4535550.html
4.共轭梯度法:
(1)思想:
介于梯度下降法和牛顿法之间的一种方法,仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。
5.参考:
https://www.cnblogs.com/shixiangwan/p/7532830.html
https://www.cnblogs.com/xiaohuahua108/p/6011105.html