函数的定义:给定一个数集A,对A施加一个对应的法则/映射f,记做:f(A),那么可以得到另外一个数集B,也就是可以认为B=f(A);那么这个关系就叫做函数关系式,简称函数。
三个重要因素:定义域A、值域B、对应的映射法则f。
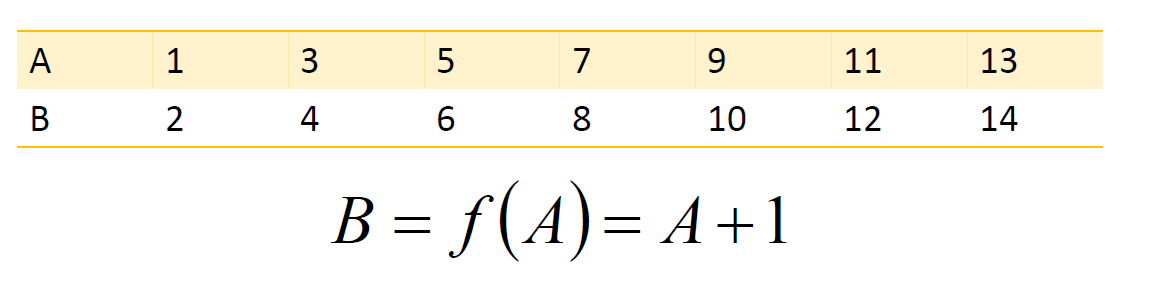
常见函数有:常函数、一次函数、二次函数、幂函数、指数函数、对数函数。
import math import numpy as np import matplotlib.pyplot as plt x = np.arange(0.05,3,0.05) #常函数 y1 = [5 for i in x] plt.plot(x,y1,linewidth = 2,label = '常函数:y = 5') #一次函数 y2 =[2 * i + 1 for i in x ] plt.plot(x,y2,linewidth = 2,label = '一次函数:y = 2x + 1') #二次函数 y3 =[1.5 * i * i - 3 * i + 1 for i in x ] plt.plot(x,y3,linewidth = 2,label = '二次函数:y = 1.5$x^2$ -3x + 1') #幂函数 y4 =[math.pow(i,2) for i in x ] plt.plot(x,y4,linewidth = 2,label = '幂函数:y =$x^2$') #指数函数 y5 =[math.pow(2,i) for i in x ] plt.plot(x,y5,linewidth = 2,label = '指数函数:y = $2^x$') #对数函数 y6 =[math.log(i,2) for i in x ] plt.plot(x,y6,linewidth = 2,label = '对数函数:y = log2(x)') plt.legend(loc = 'lower right')#显示图例大小,其中loc表示位置的; plt.grid(False)## 显示背景的网格线,False为不显示网络图 plt.show()
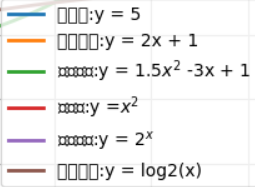
绘制的图片中文无法识别,可以在配置文件font.sans-serif中添加SimHei、FangSong等中文字体
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False#解决保存图像是负号'-'显示为方块的问题

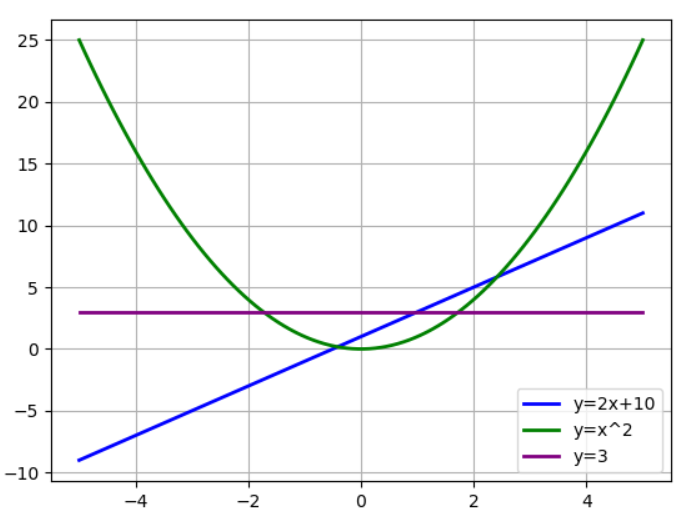
一般常见函数:
import numpy as np import matplotlib.pyplot as plt x1 = np.linspace(-5,5,100) y3 = [(2 * i + 1 )for i in x1] plt.plot(x1,y3,label = 'y=2x+10',color = 'b',linewidth = 2) y4 = [i*i for i in x1] plt.plot(x1,y4,label = 'y=x^2',color = 'g',linewidth = 2) y5 = [3 for i in x1] plt.plot(x1,y5,label = 'y=3',color = 'purple',linewidth = 2) plt.grid(True) plt.legend() plt.show()
import math import numpy as np import matplotlib.pyplot as plt x1 = np.linspace(-5,5,100) y5 = [3 * math.pow(i,3)for i in x1] plt.plot(x1,y5,label = 'y=3x^3',color = 'purple',linewidth = 2) y6 = [10/i for i in x1] plt.plot(x1,y6,label = 'y=10/x',color = 'k',linewidth = 2) plt.grid(True) plt.legend() plt.show()

三角函数:
import numpy as np import matplotlib.pyplot as plt x = np.linspace(-4*np.pi,4*np.pi,100) y = [np.sin(i)for i in x] plt.plot(x,y,label = 'y=sinx',color = 'g',linewidth = 2) y1 = [np.cos(i)for i in x] plt.plot(x,y1,label = 'y=cosx',color = 'r',linewidth = 2) plt.grid(True) plt.legend(loc='upper right') plt.xlim(-15,15) plt.show()

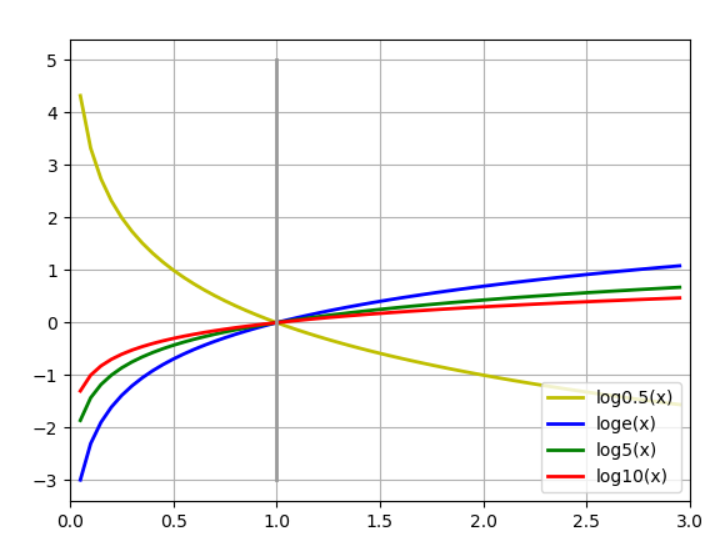
对数函数:
import math import numpy as np import matplotlib.pyplot as plt x = np.arange(0.05,3,0.05) y1 = [math.log(i,0.5)for i in x] y2 = [math.log(i,math.e)for i in x]#是以e为底的对数 y3 = [math.log(i,5)for i in x] y4 = [math.log(i,10)for i in x] plt.plot(x,y1,label = 'log0.5(x)',color = 'y',linewidth = 2) plt.plot(x,y2,label = 'loge(x)',color = 'b',linewidth = 2) plt.plot(x,y3,label = 'log5(x)',color = 'g',linewidth = 2) plt.plot(x,y4,label = 'log10(x)',color = 'r',linewidth = 2) plt.plot([1,1],[-3,5],'-',color ='#999999',linewidth = 2) plt.legend(loc='lower right') plt.xlim(0,3) plt.grid(True) plt.show()