两点之间距离
欧氏距离
即欧几里得距离。
平面内两点的距离为
立体空间内两点的距离为
(dots)
(n) 维空间内两点的距离为
曼哈顿距离
二维空间内,两点之间距离为
(n) 维空间内两点的距离为
性质 (-) 三角形不等式:从点 (i) 到 (i) 的直接距离不会大于途经的任何其它点 (k) 的距离。
切比雪夫距离
二维空间内,两点之间距离为
曼哈顿距离与切比雪夫距离的相互转化
设 (A(x_1,y_1),B(x_2,y_2)) ,
-
曼哈顿坐标系是通过切比雪夫坐标系旋转 (45^circ) 后,再缩小到原来的一半得到的
-
把每个点 ((x,y)) 转化为 ((x+y,x-y)) ,新坐标系下的切比雪夫距离 就是 原坐标系下的曼哈顿距离 。
-
把每个点 ((x,y)) 转化为 ((dfrac{x+y}{2},dfrac{x-y}{2})) ,新坐标系下的曼哈顿距离 就是 原坐标系下的切比雪夫距离 。
例题
P5098 [USACO04OPEN]Cave Cows 3
对于式子 (|x_1-x_2|+|y_1-y_2|) ,可以假设 (x_1-x_2ge 0) ,根据 (y_1-y_2) 正负分类讨论:
- (y_1-y_2ge 0) :
- (y_1-y_2< 0) :
分别求出 (x+y) 和 (x-y) 的最大、最小值之差即可。
P4648 [IOI2007] pairs 动物对数 (曼哈顿距离转切比雪夫距离)
P3964 [TJOI2013]松鼠聚会 (切比雪夫距离转曼哈顿距离)
向量叉积
对于点对 ((A,B,C)) ,设:
(x_1=A_x-B_x,y_1-A_y-B_y,x_2=C_x-B_x,y_2=C_y-B_y)
若:
则:
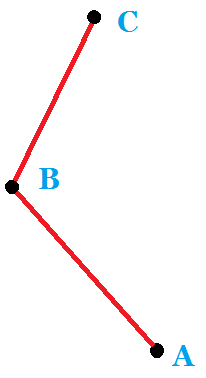
若:
则:
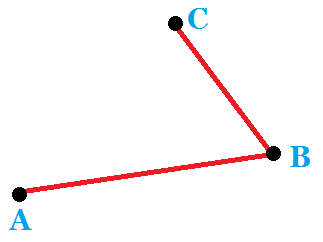
因此我们就可以利用叉积来维护凸包以及多边形面积。
点的旋转
让点 ((x_1,y_1)) 绕点 ((x_2,y_2)) 旋转 (t^o) :
(x=(x_1-x_2) imes cos{t}-(y_1-y_2) imes sin{t}+x_2)
(y=(x_1-x_2) imes sin{t}+(y_1-y_2) imes cos{t}+y_2)