Floyd算法
Floyd算法可以用来解决任意两个顶点之间的最短路径问题。
核心公式为:
Edge[i][j]=Min{Edge[i][j],Edge[i][k]+Edge[k][j]}。
即通过对i,j两个顶点之间插入顶点后比较路径的大小来进行松弛。
首先我们来定义一个二维数组Edge[MAXN][MAXN]来存储图的信息。
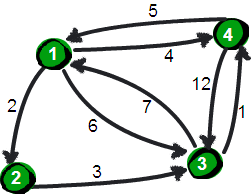
这个图的Edge数组初始化以后为
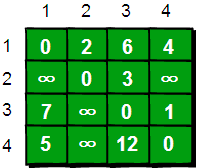
相当于任意两点之间不允许经过其他点时的距离情况。
Code1:
1 //经过1号顶点 2 for(i=1;i<=n;i++) 3 for(j=1;j<=n;j++) 4 if (e[i][j] > e[i][1]+e[1][j]) e[i][j]=e[i][1]+e[1][j];
这里表示允许一号顶点作为中间点来松弛距离,并保存松弛完的结果。
Code2:
1 //经过2号顶点 2 for(i=1;i<=n;i++) 3 for(j=1;j<=n;j++) 4 if (e[i][j] > e[i][2]+e[2][j]) e[i][j]=e[i][2]+e[2][j];
允许一号顶点和二号顶点作为中间点来松弛,并保存。(不是必定会松弛!)
。。。。。
Floyd核心代码:
1 for(k=1;k<=n;k++) 2 for(i=1;i<=n;i++) 3 for(j=1;j<=n;j++) 4 if(e[i][j]>e[i][k]+e[k][j]) 5 e[i][j]=e[i][k]+e[k][j];
这段代码的基本思想就是:最开始只允许经过1号顶点进行中转,接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转,求任意两点之间的最短路程。用一句话概括就是:从i号顶点到j号顶点只经过前k号点的最短路程。
时间复杂度:O(n^3)
部分图片文字摘自于啊哈磊的blog。