题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出orz
输入输出格式
输入格式:
第一行包含两个整数N、M,表示该图共有N个结点和M条无向边。(N<=5000,M<=200000)
接下来M行每行包含三个整数Xi、Yi、Zi,表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式:
输出包含一个数,即最小生成树的各边的长度之和;如果该图不连通则输出orz
输入输出样例
输入样例#1:
4 5 1 2 2 1 3 2 1 4 3 2 3 4 3 4 3
输出样例#1:
7
说明
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=20
对于40%的数据:N<=50,M<=2500
对于70%的数据:N<=500,M<=10000
对于100%的数据:N<=5000,M<=200000
样例解释:
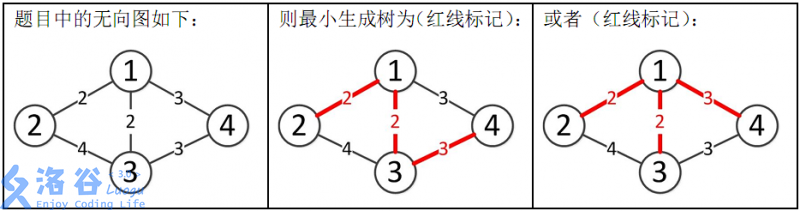
所以最小生成树的总边权为2+2+3=7
kruskal:
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #define maxn 5003 6 #define maxm 200005 7 using namespace std; 8 int read(){ 9 int x=0,f=1;char ch=getchar(); 10 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 11 while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} 12 return x*f; 13 } 14 int fa[maxn],deep[maxn]; 15 int n,m,tot=0,ans=0; 16 struct node{int u,v,w;}e[maxm]; 17 bool cmp(node a,node b){return a.w<b.w;} 18 int find(int x){ 19 if(fa[x]==x) return x; 20 else return fa[x]=find(fa[x]); 21 } 22 void unite(int x,int y){ 23 x=find(x),y=find(y); 24 if(x==y) return ; 25 if(deep[x]<deep[y]) fa[x]=y; 26 else{ 27 fa[y]=x; 28 if(deep[x]==deep[y]) deep[x]++; 29 } 30 } 31 bool same(int x,int y){ 32 return find(x)==find(y); 33 } 34 int main(){ 35 n=read(),m=read(); 36 for(int i=1;i<=n;i++) fa[i]=i,deep[i]=0; 37 for(int i=1;i<=m;i++) 38 e[i].u=read(),e[i].v=read(),e[i].w=read(); 39 sort(e+1,e+m+1,cmp); 40 for(int i=1;i<=m;i++){ 41 if(same(e[i].u,e[i].v)) continue; 42 else{ 43 unite(e[i].u,e[i].v); 44 ans+=e[i].w; 45 tot++; 46 } 47 } 48 if(tot<n-1) printf("orz"); 49 else printf("%d",ans); 50 return 0; 51 }
prim:
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<algorithm> 5 #define maxn 5005 6 #define maxm 200005 7 #define INF 0x3f3f3f3f 8 using namespace std; 9 int read(){ 10 int x=0,f=1;char ch=getchar(); 11 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 12 while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} 13 return x*f; 14 } 15 int n,m,dis[maxn],last[maxn],cnt,ans; 16 bool vis[maxn]; 17 struct node{int to,next,cost;}e[2*maxm]; 18 void add(int u,int v,int w){ 19 e[++cnt].to=v;e[cnt].next=last[u];last[u]=cnt;e[cnt].cost=w; 20 } 21 void prim(){ 22 for(int i=1;i<=n;i++) dis[i]=INF; 23 dis[1]=0; 24 for(int j=1;j<=n;j++){ 25 int u=-1,minn=INF; 26 for(int i=1;i<=n;i++){ 27 if(dis[i]<minn&&!vis[i]){ 28 u=i; 29 minn=dis[i]; 30 } 31 } 32 if(u==-1){ 33 ans=-1; 34 return ; 35 } 36 vis[u]=1; 37 ans+=dis[u]; 38 for(int i=last[u];i;i=e[i].next){ 39 int v=e[i].to; 40 if(!vis[v]&&dis[v]>e[i].cost) dis[v]=e[i].cost; 41 } 42 } 43 } 44 int main(){ 45 n=read(),m=read(); 46 for(int i=1;i<=m;i++){ 47 int u=read(),v=read(),w=read(); 48 add(u,v,w); 49 add(v,u,w); 50 } 51 prim(); 52 if(ans==-1) printf("orz "); 53 printf("%d ",ans); 54 return 0; 55 }