满二叉树
通过名字就可以看出来是一个满的二叉树,意思也就是二叉树上每一层的结点数都达到了最大。看上去就像上个三角形。

满二叉树必须满足:
1.总的结点个数2k-1个结点; 如上图是一个3层的二叉树,总的结点个数为23-1=7个点节
2.第i层的结点个数数为2k-1个结点;如上图第3层的结点个数为23-1=4个结点
3.具有n个节点的满二叉树的深度为log2(n+1),如上图节点数为7,log2(7+1)=3,深度为3。
完全二叉树
和满二叉树不同的是最后一层不是满的,除了最了一层,其余的k-1层是一个满二叉树,最后一层的结点是从左开始排列的。(满二叉树是特殊的完全二叉树,但完全二叉树不一定是满二叉树)

完全二叉树必须满足:
1.某个节点没有左子节点,那么肯定也不能有右子节点
2.从第1层到第k-1层是一个满二叉树,最后一层的结点从左开始排列。
二叉查找树
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
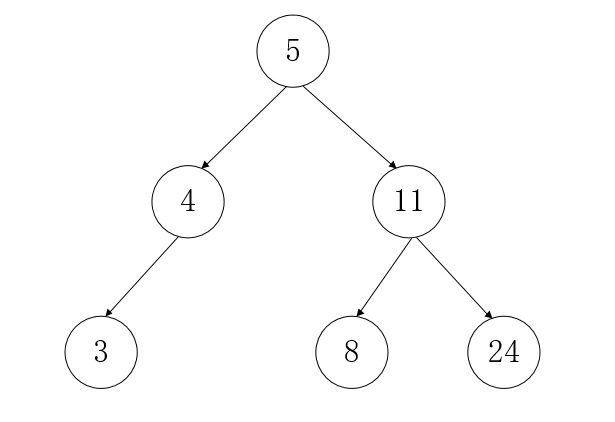

最优 最坏
二叉查找树必须满足:
1.所有子树上面的左节点的值都比根结点要小,右节点的值都比根结点要大
2.任意结点的左右子树也都是二叉查找树
3.通过中序遍历,将得到的是一个有序的数列
对其操作的最优的时间复杂度为O(log2n),相当于对数列进行二分查找法。最坏的时间复杂度为O(n),相当于线性查找。
平衡二叉树
平衡二叉树(Balanced Binary Tree)又被称为AVL树(有别于AVL算法),它是二叉查找树最优的情况。它很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多。
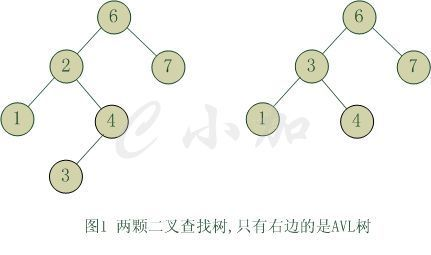
且具有以下性质:
1.它是一个二叉查找树
2.它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
3.当删除、新增、修改节点上的值时,它会通过左旋或右旋的操作使二叉树保持平衡。
4.最坏的时间复杂度为O(log2n)
如果对左旋和右旋操作不了解的可以看:https://www.cnblogs.com/zhangbaochong/p/5164994.html ,一些操作很详细。
红黑树
它是一种二叉查找树,但在每个节点增加一个存储位表示节点的颜色,可以是红或黑(非红即黑)。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,红黑树确保没有一条路径会比其它路径长出两倍(这里是和平衡二叉树的主要区别),因此,红黑树是一种弱平衡二叉树(由于是弱平衡,可以看到,在相同的节点情况下,AVL树的高度低于红黑树),相对于要求严格的AVL树来说,它的旋转次数少,所以对于搜索,插入,删除操作较多的情况下,我们就用红黑树。如果应用场景中对插入删除不频繁,只是对查找要求较高,那么AVL还是较优于红黑树。
更详细的红黑树介绍:https://www.cnblogs.com/skywang12345/p/3245399.html

红黑树与平衡二叉树的区别:
1、红黑树放弃了追求完全平衡,追求大致平衡,在与平衡二叉树的时间复杂度相差不大的情况下,保证每次插入最多只需要三次旋转就能达到平衡,实现起来也更为简单。
2、平衡二叉树追求绝对平衡,条件比较苛刻,实现起来比较麻烦,每次插入新节点之后需要旋转的次数不能预知。
3、红黑树和AVL树的区别在于它使用颜色来标识结点的高度,它所追求的是局部平衡而不是AVL树中的非常严格的平衡。
4、红黑树是牺牲了严格的高度平衡的优越条件为代价红黑树能够以O(log2 n)的时间复杂度进行搜索、插入、删除操作。
5、红黑树的算法时间复杂度和AVL相同,但统计性能比AVL树更高.
二叉树遍历
分为三种:前序、中序、后序,其中序遍历最为重要。为啥叫这个名字?是根据根节点的顺序命名的。
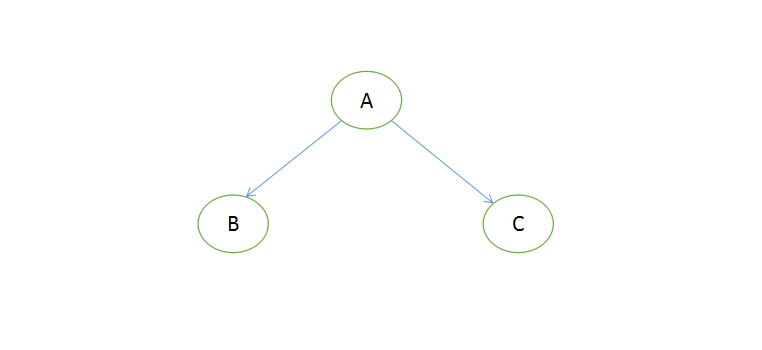
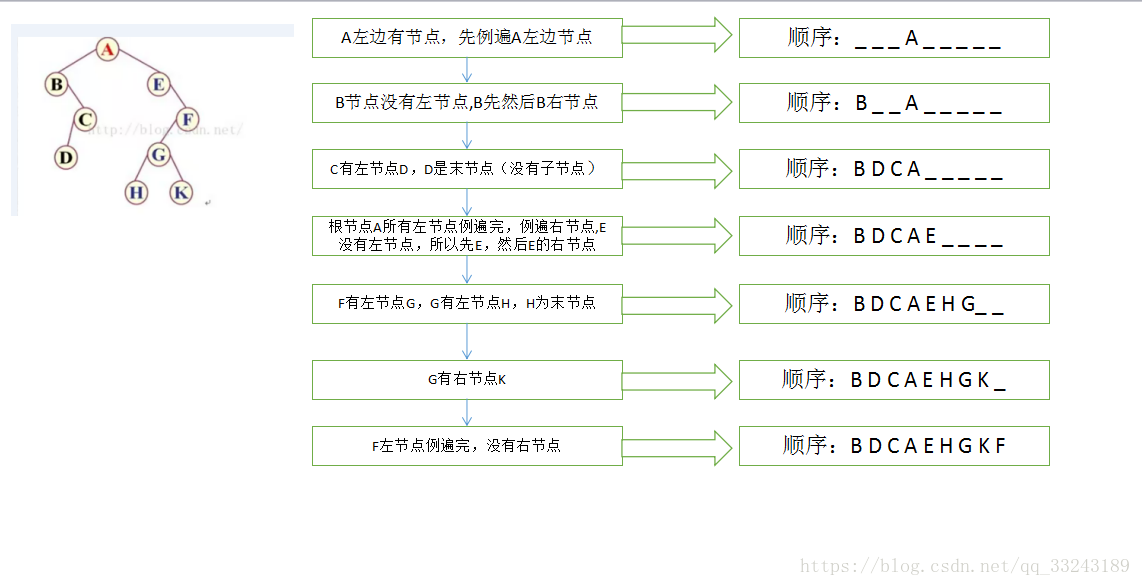
比如上图正常的一个满节点,A:根节点、B:左节点、C:右节点,前序顺序是ABC(根节点排最先,然后同级先左后右);中序顺序是BAC(先左后根最后右);后序顺序是BCA(先左后右最后根)。
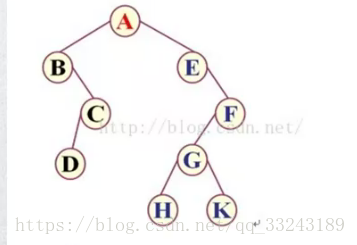
比如上图二叉树遍历结果
前序遍历:ABCDEFGHK
中序遍历:BDCAEHGKF
后序遍历:DCBHKGFEA
分析中序遍历如下图,中序比较重要(java很多树排序是基于中序,后面讲解分析)