关于这题,先看看官方的解释:地球人都知道整点是不能构成正五边形和正三边形和正六边形的,所以只需暴力枚举四个点判断是否是正四边形即可。假如你不是地球人,那么即使暴力枚举正三边 形和稍微不那么暴力地找正五边形和正六边形也是可以通过的(反正找不到)。
那么很明显,接下来要思考就是如何找正四边形,只找四条相连且相等的边是不够的,因为四边相连且相等的可能是菱形,不是正四边形。
我的思路参考了比赛中Hezhu提交的代码:
1.寻找四条边的每条边要么平行x轴,要么平行y轴的正四边形。以一个点为基准点(x, y),算做是正四边型中的一个点,然后枚举长度r,寻找是否存在(x+r, y)(x, y+r)(x+r, y+r).
2.寻找每条边并不平行x轴或y轴的正四边形,也是找基准点,枚举长度,我把自己画的图放上来了:
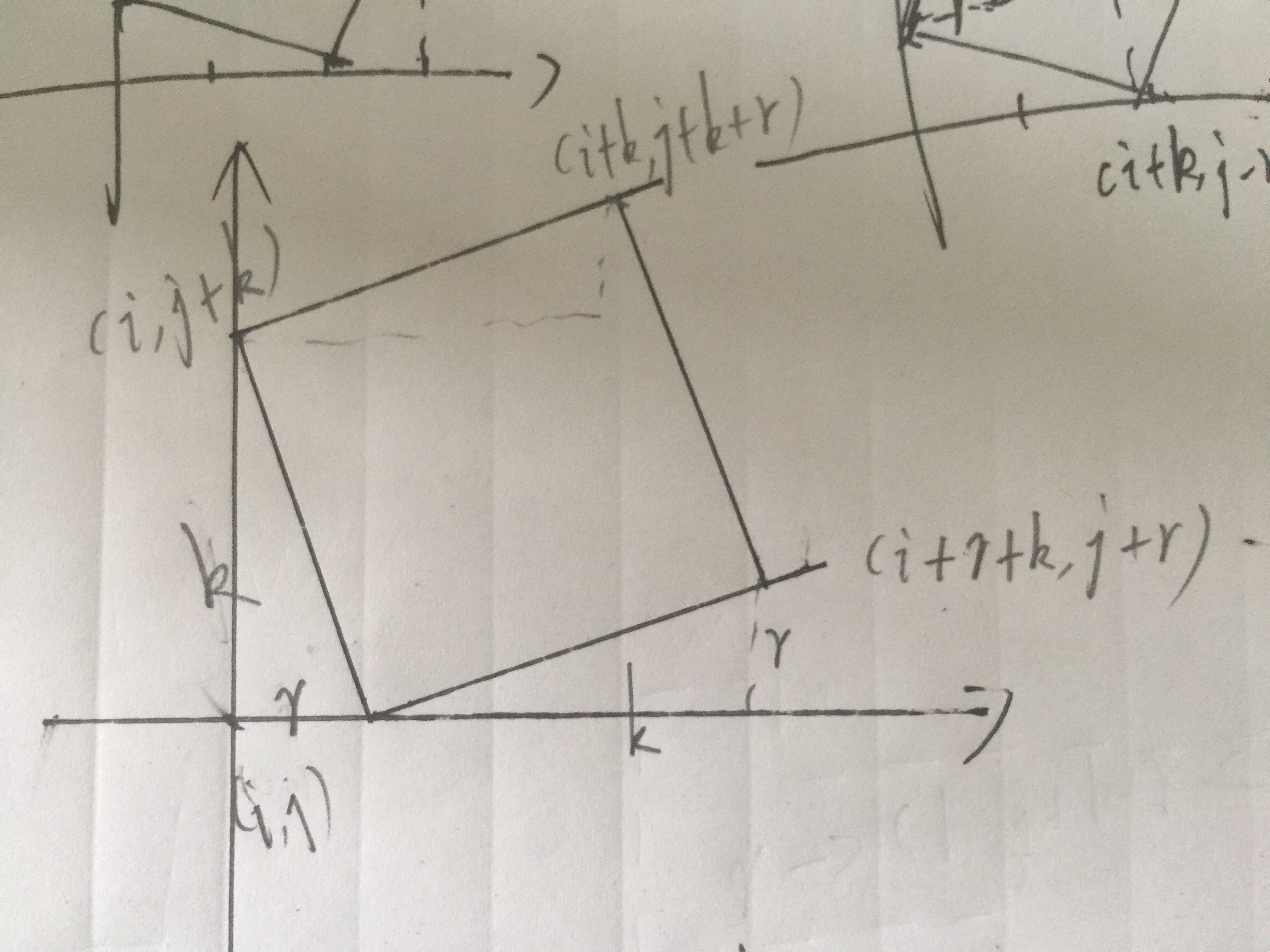
以(i, j)为基准点,枚举长度,k,r依旧是寻找能构成正四边形的四个点是否存在。
一点感悟:比赛时,其实有质疑整点是否能形成正三边形,正五边形,正六边形,但是一时间无法证明整点不能构成这三种正边形,于是就思考如何暴力求解,正三、四、五、六边形。比赛后,才发现,自己的质疑其实是有道理的,只是当时选择了保守方案。话说,比赛的时候,一直在想用递归求解,但在知道只有四边形后,不知道为什么却还在思考如何用递归求解,直至看了别人的代码,才发现自己有点舍近求远了。
import java.util.Arrays;
import java.util.Scanner;
/**
* Created by emerald on 8/11/15.
* hdu 5365
*/
public class Main {
public static void main(String []args) {
Scanner in = new Scanner(System.in);
boolean vis[][] = new boolean[15][15];
int N;
while(in.hasNext()) {
N = in.nextInt();
for(int i=0; i<15; ++i) {
for(int j=0; j<15; ++j) {
vis[i][j] = false;
}
}
int x, y;
for(int i=0; i<N; ++i) {
x = in.nextInt();
y = in.nextInt();
vis[x][y] = true;
}
int ans = 0;
// 1
for(int i=0; i<9; ++i) {
for(int j=0; j<9; ++j) {
for(int r=1; r+i<9 && r+j<9; ++r) {
if(vis[i][j] && vis[i+r][j] && vis[i][j+r] && vis[i+r][j+r]) {
++ ans;
}
}
}
}
// 2
for(int i=0; i<9; ++i) {
for(int j=0; j<9; ++j) {
for(int r=1; r<9; ++r) {
for(int k=1; j+k+r<9 && i+r+k<9; ++ k) {
if(vis[i][j+k] && vis[i+r][j] && vis[i+k][j+k+r] && vis[i+r+k][j+r]) {
++ ans;
}
}
}
}
}
System.out.println(ans);
}
}
}