抓住czx

抓住czx

洛谷P4880 抓住czx

前言（吐槽 珂忽略）

这道题说来都心酸，在第一次得到(T=0)的(30pt)s后，开始肝正解

但是在判断的时候忽略了一种情况（我并没有意识到），一直卡在了(90pts)，甚至还发了贴去求助（然而并没有人回我QAQ）

后来在同桌的帮助下，意识到了缺少一种情况，然后自己想出了这种情况怎么处理，但是.....因为手贱多写了一个“(=)”，又在#1和#2反复横跳（我真惨菜）

最后耐心地又敲了一遍，才艰难的A掉了这道并不难的蓝题

---

解题思路

好了，吐槽完了，开始正题吧

• (T=0)的特殊情况

只要会求最短路的，应该都没问题吧，(30pts)给得死死的

多说一点：(T=0)意味着(czx)不会瞬移，则(czx)一直在(e)这个位置，那抓住他的最短时间自然就是从(b)到(e)的最短路长度咯

• 完整正解

在除(T=0)的特殊情况外，也会存在一种情况不用考虑瞬移：我们在(czx)第一次瞬移之前就抓住了他，即从(b)到(e)的最短路长度(＜)第一次瞬移的时间

注意一下，这里的“第一次”并不是指输入的第一组瞬移数据，而是排序后的第一次（即我们将所有瞬移按照时间节点从早到晚排序后的第一次瞬移）

之后的情况就都是需要考虑瞬移的了（我们用(dis[i])表示从(1)到(i)的最短时间）

设(czx)第(i)次瞬移到的点为(pi)、时间为(ti)

• 若(dis[pi]≤ti)，说明我们在第(i)次瞬移后抓住了他

这里可能大家会疑惑：为什么是“(≤)”而不是“(＜)”？题目中不是说在一个瞬移时间点，总是(czx)先瞬移走，然后我们才到，这样是抓不住的啊

题目中确实说明了这一点，但是这个规则并不影响我们的这个判断，而是影响我们下面的另一个判断（下面会着重点出）

然后，我们再来解释一下这个判断的原理（也能解释上面的疑惑）：

1. 若我们比(czx)先到达(pi)这个点（对应(dis[pi])(＜)(ti)），那我们就在(pi)这个点等着抓他就好了（守株待兔嘛）

2. 若我们和(czx)同时到达(pi)这个点（对应(dis[pi])(＝)(ti)），那我们就正好抓住他

• 若(dis[pi]>ti),说明我们无法在(pi)这个点抓住(czx)，但是也需要加以讨论

（这就是我一直忽略的情况，下面给出图来帮助理解）

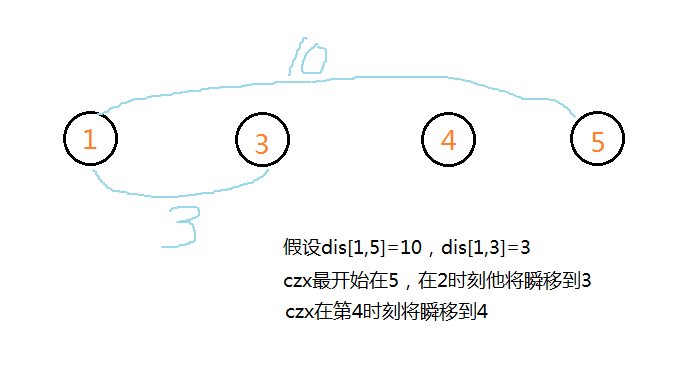
在第(2)时刻，(czx)已经到达点(3)，而我们还在从(1)到(3)的路上，那显然是(dis[pi]>ti)的情况

但是在第(3)时刻我们到达了(czx)所在的点(3)，而此时(czx)还没有进行下一次的瞬移，所以我们抓住了他

面对上面这种情况，我们单单因为(dis[pi]>ti)的话，就会错失掉在第(3)时刻抓住(czx)的机会！所以我们还需要加个判断防止误判：(dis[a[i].p]<a[i+1].t)

还是来解释一下原理：如果我们到达(pi)这个点的时间在(czx)下一次瞬移之前，那我们依旧能够抓住他，所以这种情况答案就是我们到达(pi)的时间

再着重讲一下为什么这里就是“(<)”而不是“(≤)”，正如上面的疑惑，题目中说定了在一个瞬移的时间点，总是(czx)先瞬移然后我们再到达。所以当我们到达(pi)时，(czx)已经瞬移走了，故我们抓不住他（请大家注意区分qwq）

---

代码Code

#include <bits/stdc++.h>
using namespace std;
priority_queue<pair<int,int> > q;
int n,m,t,b,E,x,y,z;
int tot,dis[1000010],vis[1000010],head[1000010];

struct node {
	int to,net,val;
} e[1000010];

struct nodes {
	int t,p;
} a[1000010];

inline void add(int u,int v,int w) {
	e[++tot].to=v;
	e[tot].val=w;
	e[tot].net=head[u];
	head[u]=tot;
}

inline void dijkstra(int s) {  //Dijkstra求最短路板子 
	for(register int i=1;i<=n;i++) {
		vis[i]=0;
		dis[i]=2005020600;
	}
	dis[s]=0;
	q.push(make_pair(0,s));
	while(!q.empty()) {
		int x=q.top().second;
		q.pop();
		if(vis[x]) continue;
		vis[x]=1;
		for(register int i=head[x];i;i=e[i].net) {
			int v=e[i].to;
			if(dis[v]>dis[x]+e[i].val) {
				dis[v]=dis[x]+e[i].val;
				q.push(make_pair(-dis[v],v));
			}
		}
	}
}

inline bool cmp(nodes x,nodes y) {
	return x.t<y.t;
}

int main() {
	scanf("%d%d%d%d",&n,&m,&b,&E);
	for(register int i=1;i<=m;i++) {
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);
		add(y,x,z);
	}
	scanf("%d",&t);
	for(register int i=1;i<=t;i++) {
		scanf("%d%d",&a[i].t,&a[i].p);
	}
	sort(a+1,a+1+t,cmp);   //将所有瞬移按照时间点从早到晚排序 
	dijkstra(b);
	if(dis[E]<a[1].t||t==0) {  //不用管瞬移的两种情况 
		printf("%d",dis[E]);
		return 0;
	}
	for(register int i=1;i<=t;i++) {  //枚举瞬移找答案 
		if(dis[a[i].p]<=a[i].t) {  //守株待兔或正好抓住的情况 
			printf("%d",a[i].t);
			return 0;
		}
		else {
			if(dis[a[i].p]<a[i+1].t) {  //在下一次瞬移前抓住的情况 
				printf("%d",dis[a[i].p]);
				return 0;
			}
		}
	}
	return 0;
}

---

最后，如果有任何地方不懂或不对的，欢迎大家在评论区留言，我会及时回复，谢谢大家啊qwq

---