暑假第二十七测

题解：

第一题，水题，把点拆了，dis[i][j]表示当前在i点经过了j个城市的最小距离，然后建一个大的S,T，跑一遍SPFA就可以了，dijstra巨慢（好多人都被卡了，数据很绝）；

#include<bits/stdc++.h>
using namespace std;
const int M = 2005, ME = 1e5;
const int inf = 2e9;
int h[M], s[M], t[M], d[M][M], a[M], b[M], S, T, tot, inq[M][M];
struct sta{
    int x, v, dis;
    bool operator < (const sta &rhs) const{
        return v == rhs.v ? dis > rhs.dis : v > rhs.v;
    }
};
struct edge{int nxt, v, w;}G[ME];
void add(int u, int v, int w){
    G[++tot].v = v; G[tot].nxt = h[u]; G[tot].w = w; h[u] = tot;
}



queue <sta> q;

int main(){
    
    freopen("park.in","r",stdin);
    freopen("park.out","w",stdout);
    int V, M, N, E, L;
    scanf("%d%d%d%d%d", &V, &M, &N, &E, &L);
    S = 0, T = V + 1;
    for(int i = 1; i <= M; i++){
        scanf("%d%d", &s[i], &a[i]);
        add(S, s[i], a[i]);
    }
    for(int i = 1; i <= N; i++){
        scanf("%d%d", &t[i], &b[i]);
        add(t[i], T, b[i]);
    }
    for(int i = 1; i <= E; i++){
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w);
    }
    
    for(int i = 0; i <= T; i++)
        for(int j = 0; j <= T; j++)
            d[i][j] = inf;
    int ts = 0;
    q.push((sta){S, 0});inq[S][0] = 1; d[S][0] = 0;
    while(!q.empty()){
        sta u = q.front(); q.pop(); inq[u.x][u.v] = 0;
        for(int i = h[u.x]; i; i = G[i].nxt){
            if(d[G[i].v][u.v + 1] > d[u.x][u.v] + G[i].w && d[u.x][u.v] + G[i].w <= L){
                d[G[i].v][u.v + 1] = d[u.x][u.v] + G[i].w;
                if(!inq[G[i].v][u.v + 1])inq[G[i].v][u.v + 1] = 1, q.push((sta){G[i].v, u.v + 1});
            }
        }
    }
    for(int i = T; i; i--)if(d[T][i] <= L){ts = i;break;}
    //int vv=clock();
    //cout<<cc-tt<<" "<<vv-cc<<endl;
    printf("%d
", max(0, ts - 1));
}

第二题：处理出当前点向右延展第一次可以到那pos[i],那么他随便向右延展都可以；

所以对于一个查询我们二分找到pos[i]<=rg的最大lf,那么他前面的点都可以；

贡献就是sum( posi - i + R - i) * （R - posi +1) / 2 - i * (R - posi + 1) * i;

把式子拆了就成了 1/2 * (  sum(R*R + R  + 2i * (r + 1) )  + sum(posi - posi*posi+ 2*i*posi) )

前面是常数，后面用前缀和维护；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int M = 1e6 + 10;
int tmp, cnt, a[M], vis[M], n;
void add(int c, int d){
    vis[c]+=d;
    if(vis[c] == 1 && d > 0)tmp++;
    if(!vis[c] && d < 0)tmp--;
}
ll sum[M], gx[M], pos[M];
ll binary(ll lf, ll rg, ll k){
    ll ans = 0;
    while(lf <= rg){
        ll mid = (lf + rg) >> 1;
        if(pos[mid] <= k)ans = mid, lf = mid + 1;
        else rg = mid - 1;
    }
    return ans;
}
int main(){
    freopen("plan.in","r",stdin);
    freopen("plan.out","w",stdout);
    int m, q;
    scanf("%d%d%d", &n, &m, &q);
    for(int i = 1; i <= n; i++)scanf("%d", a + i);
    int s, t = 0;
    for(s = 1; s <= n;){
        while(tmp < m && t <= n)add(a[++t], 1);
        if(t > n)break;
        pos[s] = t;
        add(a[s], -1);s++;
    }
    for(; s <= n; s++)pos[s] = n + 1;
    for(int i = 1; i <= n; i++){
        gx[i] = pos[i] - pos[i]*pos[i] + 2*i*1LL*pos[i];
        sum[i] = sum[i - 1] + gx[i];
    }
    while(q--){
        ll l, r;
        scanf("%I64d%I64d", &l, &r);
        ll k = binary(l, r, r);
        if(!k){
            printf("0
");continue;
        }
        ll r1 = 1LL*(k - l + 1) * (r*r + r);
        ll r2 = -1LL*(r + 1) * (l + k) * (k - l + 1);
        ll ans = sum[k] - sum[l - 1] + r1 + r2;
        printf("%I64d
",ans/2);    
        
    }
}

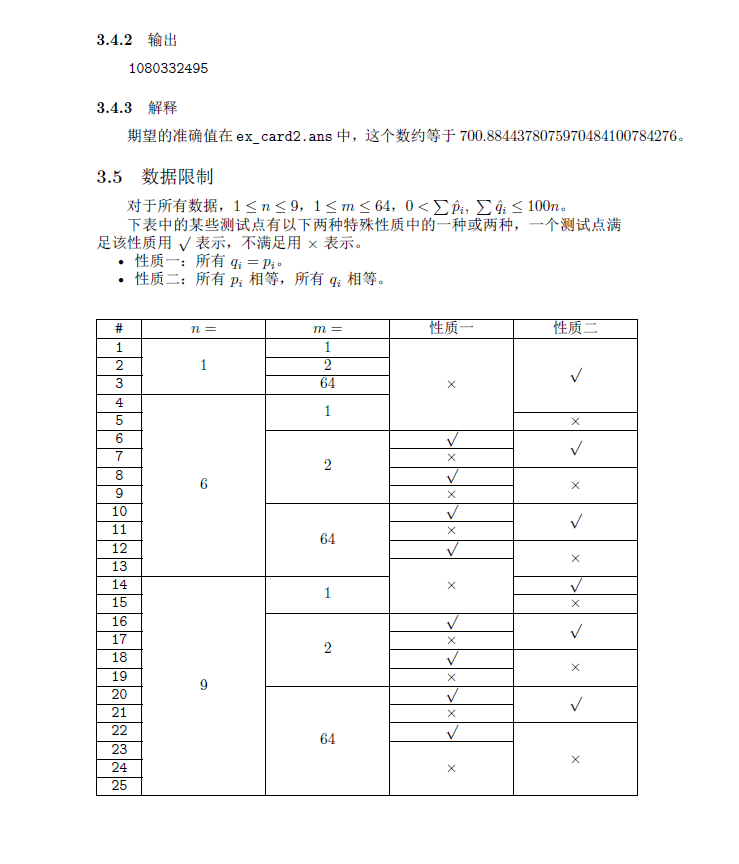
第三题：期望+状压，又是恶心数论，还是看懂了题解写不出码的那种，直接贴标准code

#define FIO "card"
#include <cstdio>
#define N_MAX 9
#define M_MAX 64
#define S_MAX (1 << (N_MAX << 1))
typedef unsigned long long lnt;
typedef unsigned unt;
const unt P = 2000000011;
inline lnt moc(lnt a) { return a < P ? a : a - P; }
inline lnt qow(lnt a, unt k)
{
    static lnt w;
    for (w = 1; k; a = a * a % P, k >>= 1)
        if (k & 1) w = w * a % P;
    return w;
}
inline lnt inv(lnt a) { return qow(a, P - 2); }
const lnt a3[4] = {0, inv(3), moc(2 * inv(3)), 1};
int n, m, i, k, s;
struct dat { lnt a, b; } e[M_MAX + 1];
lnt u, v, p[N_MAX + 1], q[N_MAX + 1], r[N_MAX + 1], f[S_MAX + 1][M_MAX + 1];
int main()
{
    freopen(FIO ".in", "r", stdin);
    freopen(FIO ".out", "w", stdout);
    scanf("%d %d", &n, &m);
    v = inv(100 * n);
    p[n] = 1;
    for (i = 0; i < n; ++i)
        scanf("%d", &k), p[i] = k * v % P, p[n] = moc(p[n] - p[i] + P);
    q[n] = 1;
    for (i = 0; i < n; ++i)
        scanf("%d", &k), q[i] = k * v % P, q[n] = moc(q[n] - q[i] + P);
    for (s = (1 << (n << 1)) - 2; s >= 0; --s)
    {
        e[m] = (dat) {1, 0};
        u = q[n], v = 0;
        for (i = 0; i < n; ++i)
        {
            u = moc(u + q[i] * a3[s >> (i << 1) & 3] % P);
            if ((s >> (i << 1) & 3) < 3)
                v = (v + q[i] * a3[(s >> (i << 1) & 3) ^ 3] % P * f[s + (1 << (i << 1))][m]) % P;
        }
        e[m - 1] = (dat) {u * e[m].a % P, (u * e[m].b + v) % P};
        u = p[n];
        for (i = 0; i < n; ++i)
        {
            u = (u + p[i] * a3[s >> (i << 1) & 3]) % P;
            if ((s >> (i << 1) & 3) < 3)
                r[i] = p[i] * a3[(s >> (i << 1) & 3) ^ 3] % P;
        }
        for (k = m - 2; k >= 0; --k)
        {
            v = 0;
            for (i = 0; i < n; ++i)
                if ((s >> (i << 1) & 3) < 3)
                    v = (v + r[i] * f[s + (1 << (i << 1))][k + 1]) % P;
            e[k] = (dat) {u * e[k + 1].a % P, (u * e[k + 1].b + v) % P};
        }
        f[s][0] = inv(moc(1 - e[0].a + P)) * (e[0].a + e[0].b) % P;
        f[s][m] = moc(f[s][0] + 1);
        for (k = 1; k < m; ++k)
            f[s][k] = (e[k].a * f[s][m] + e[k].b) % P;
    }
    printf("%d
", int(f[0][m]));
    return 0;
}