P3958 奶酪
输入输出样例
说明

题解:广搜或并查集

#include <bits/stdc++.h> using namespace std; const int maxn = 1005; #define ll long long ll x[maxn], y[maxn], z[maxn], tot; bool vis[maxn]; int h[maxn]; void read(ll &x){ ll f=1;x=0;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} x*=f; } void init(){ memset(vis, 0, sizeof(vis)); memset(h, 0, sizeof(h)); tot = 0; } struct edge{int v, nxt;}G[maxn*maxn]; void add(int u, int v){ G[++tot].nxt = h[u]; G[tot].v = v; h[u] = tot; G[++tot].nxt = h[v]; G[tot].v = u; h[v] = tot; } void bfs(){ queue <int> Q; Q.push(0); vis[0] = 1; while(!Q.empty()){ int u = Q.front(); Q.pop(); for(int i = h[u]; i; i = G[i].nxt){ int v = G[i].v; if(!vis[v]){Q.push(v); vis[v] = 1;} } } } bool adjoint(int i, int j, ll r){ long double t = (long double)((x[i]-x[j])*(x[i]-x[j]) + (y[i]-y[j])*(y[i]-y[j]) + (z[i]-z[j])*(z[i]-z[j])); return t <= 4*r*r; } int main() { //freopen("cheese.in","r",stdin); //freopen("cheese.out","w",stdout); int T; scanf("%d",&T); while(T--){ int n; ll h, r; scanf("%d",&n); read(h), read(r); init(); for(int i = 1; i <= n; i++)read(x[i]), read(y[i]), read(z[i]); for(int i = 1; i <= n; i++){ if(z[i] - r <= 0)add(i, 0); if(z[i] + r >= h)add(n+1, i); for(int j = i+1; j <= n; j++) if(adjoint(i, j, r))add(i, j); } bfs(); if(vis[n+1])puts("Yes"); else puts("No"); } return 0; }
P3959 宝藏
题目描述
参与考古挖掘的小明得到了一份藏宝图,藏宝图上标出了 nn 个深埋在地下的宝藏屋, 也给出了这 nn 个宝藏屋之间可供开发的 mm 条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是,每个宝藏屋距离地面都很远, 也就是说,从地面打通一条到某个宝藏屋的道路是很困难的,而开发宝藏屋之间的道路 则相对容易很多。
小明的决心感动了考古挖掘的赞助商,赞助商决定免费赞助他打通一条从地面到某 个宝藏屋的通道,通往哪个宝藏屋则由小明来决定。
在此基础上,小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路,小明就会与考古队一起挖掘出由该条道路 所能到达的宝藏屋的宝藏。另外,小明不想开发无用道路,即两个已经被挖掘过的宝藏 屋之间的道路无需再开发。
新开发一条道路的代价是: L* K
L代表这条道路的长度,K代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋) 。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路,使得工程总代 价最小,并输出这个最小值。
输入输出格式
输入格式:
第一行两个用空格分离的正整数 n,mn,m ,代表宝藏屋的个数和道路数。
接下来 mm 行,每行三个用空格分离的正整数,分别是由一条道路连接的两个宝藏 屋的编号(编号为 1-n1−n),和这条道路的长度 vv 。
输出格式:
一个正整数,表示最小的总代价。
输入输出样例
说明

题解:状压dp, 方程很简单,但实现起来很多细节
dp[s][j] 表示经过了那些地方s, j表示现在停在那里;
dp[s][i] = max(dp[s^i][j] + mp[j][i] * dis[s^i][j]); dis表示在当前状态下,j离根的距离; O(2^n * n^2)
注意: 当dis[s][ i ] 更新完以后,其他的dis[s][ ] 也要复制一下,最开始忘了;

#include <bits/stdc++.h> using namespace std; const int inf = 1000000008, maxn = 1<<14; int dp[maxn], sta[maxn][15], mp[15][15]; bool inq[15]; int n, m, ans = inf; void init(){ memset(dp, 127, sizeof(dp)); memset(sta, 127, sizeof(sta)); } void read(int &x){ int f=1;x=0;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} x*=f; } int main() { // freopen("treasure.in","r",stdin); // freopen("treasure.out","w",stdout); scanf("%d%d",&n, &m); memset(mp, 127, sizeof(mp)); for(int i = 1; i <= m; i++){ int u, v, w; read(u), read(v), read(w); if(mp[u][v] > w)mp[u][v] = mp[v][u] = w; } for(int st = 1; st <= n; st++){ init(); dp[1<<(st-1)] = 0; for(int s = 1<<(st-1); s < (1<<n); s++){ if((s&(1<<(st-1))) == 0)continue; sta[s][st] = 1; for(int i = 1; i <= n; i++) if((s&(1<<(i-1))) == 0) for(int j = 1; j <= n; j++)//gao wei if(s&(1<<(j-1)) && mp[j][i] < inf && sta[s][j] < inf){ int t = dp[s] + sta[s][j] * mp[j][i]; if(t < dp[s|(1<<(i-1))]){ dp[s|(1<<(i-1))] = t; for(int p=1;p<=n;p++) sta[s|(1<<(i-1))][p] = sta[s][p]; sta[s|(1<<(i-1))][i] = sta[s][j] + 1; } } } // if(st == 3) for(int s = 1; s <(1<<n); s++)printf("dp[%d] = %d ",s,dp[s]); // cout<<dp[(1<<n)-1]<<" "<<st<<endl; ans = min(ans, dp[(1<<n)-1]); } printf("%d ",ans); return 0; }
dfs版,不用复制,跑的快一些;

#include <bits/stdc++.h> using namespace std; const int inf = 1000000008, maxn = 1<<14; int dp[maxn], dis[15], mp[15][15]; bool inq[15]; int n, m, ans = inf; void init(){ memset(dp, 127, sizeof(dp)); memset(dis, 0, sizeof(dis)); } void dfs(int s){ for(int i = 1; i <= n; i++){ if(s&(1<<(i-1)))continue; for(int j = 1; j <= n; j++) if(s&(1<<(j-1)) && mp[i][j] < inf){ int t = dp[s] + dis[j] * mp[i][j]; if(t < dp[s|(1<<(i-1))]){ int tmp = dis[j]; dis[i] = dis[j] + 1; dp[s|(1<<(i-1))] = t; dfs(s|(1<<(i-1))); dis[i] = tmp; } } } } void read(int &x){ int f=1;x=0;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} x*=f; } int main() { //freopen("treasure.in","r",stdin); //freopen("treasure.out","w",stdout); scanf("%d%d",&n, &m); memset(mp, 127, sizeof(mp)); for(int i = 1; i <= m; i++){ int u, v, w; read(u), read(v), read(w); if(mp[u][v] > w)mp[u][v] = mp[v][u] = w; } for(int st = 1; st <= n; st++){ init(); dp[1<<(st-1)] = 0; dis[st] = 1; dfs(1<<(st-1)); ans = min(ans, dp[(1<<n)-1]); //cout<<" "<<dp[(1<<n)-1]<<" "<<st<<endl; } printf("%d ",ans); return 0; }
P3953 逛公园

输入输出样例
2 5 7 2 10 1 2 1 2 4 0 4 5 2 2 3 2 3 4 1 3 5 2 1 5 3 2 2 0 10 1 2 0 2 1 0
3 -1
说明
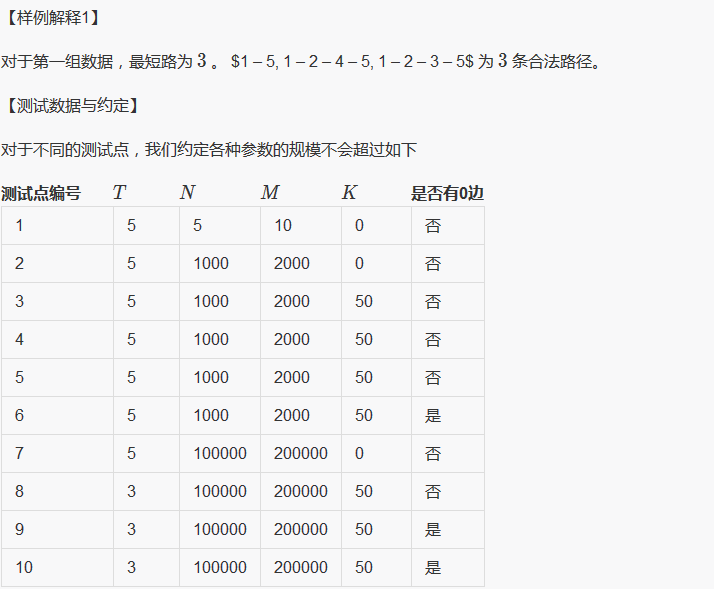
题解:dp, dp[u][k]表示现在在u这个节点,还有k可以拿去随便挥霍的方案数;
dp[u][k] += dp[v][ k + dis[v] - dis[u] + G[i].w ], dis是到1的最短路,然后枚举k,dfs;
两个地方:由于可以跑回去所以不能在终点设置边界;多放一个虚点,用来设置边界;
对于无限跑环的是因为有0边存在,不然总会停的,跑0边的条件是从dp[u][k] 又跑到dp[u][k], 所以用一个ins来记录状态,防止死循环

#include <bits/stdc++.h> using namespace std; int n,m,k,p,tot,tot2; const int maxn = 100005, inf = 2000000008; const int maxm = maxn*2; int dis[maxn],hh[maxn],h[maxn],dp[maxn][55]; bool vis[maxn],inq[maxn],ins[maxn][55]; struct edge{int v,w,nxt;}G[maxm],g[maxm]; struct Node{ int v, dis; bool operator < (const Node &a)const{ return dis > a.dis; } }; void dij(){ priority_queue <Node> q; q.push(Node{n+1, 0}); memset(dis, 127, sizeof(dis)); memset(vis, 0, sizeof(vis)); dis[n+1] = 0; while(!q.empty()){ Node u = q.top(); q.pop(); if(vis[u.v])continue; vis[u.v] = 1; for(int i = hh[u.v]; i; i = g[i].nxt){ int v = g[i].v; if(!vis[v] && dis[v] > dis[u.v] + g[i].w){ dis[v] = dis[u.v] + g[i].w; q.push(Node{v, dis[v]}); } } } } int dfs(int u, int kk){ if(ins[u][kk])return inf; if(dp[u][kk] != -1)return dp[u][kk]; ins[u][kk] = 1; dp[u][kk] = 0; for(int i = h[u]; i; i = G[i].nxt){ int v = G[i].v; int pp = dis[u] + kk - dis[v] - G[i].w; if(pp < 0)continue; if(dfs(v, pp) == inf)return dp[u][kk] = inf; dp[u][kk] = (dp[u][kk] + dp[v][pp]) % p; } ins[u][kk] = 0; return dp[u][kk]; } void add2(int u,int v,int w){G[++tot2].nxt=h[u];G[tot2].v=v;G[tot2].w=w;h[u]=tot2;} void add1(int u,int v,int w){g[++tot].nxt=hh[u];g[tot].v=v;g[tot].w=w;hh[u]=tot;} void init(){ memset(h,0,sizeof(h)); memset(hh,0,sizeof(hh)); memset(ins, 0, sizeof(ins)); tot = tot2 = 0; for(int i = 0; i <= k; i++) for(int j = 1; j <= n; j++)dp[j][i] = -1; for(int i = 1; i <= k; i++) dp[n+1][i] = 0; dp[n+1][0] = 1; } int main() { int t; scanf("%d",&t); while(t--){ scanf("%d%d%d%d",&n,&m,&k,&p); init(); for(int i = 1; i <= m; i++){ int u,v,w; scanf("%d%d%d",&u,&v,&w); add2(u, v, w); add1(v, u, w); } add1(n+1, n, 0);add2(n, n+1, 0); dij(); int ans = 0; for(int i = 0; i <= k; i++){ int t = dfs(1, i); if(t == inf){ans = -1; break;} ans = (ans + t) % p; } printf("%d ",ans); } return 0; }

