暑假第二测

题解：

第一题：

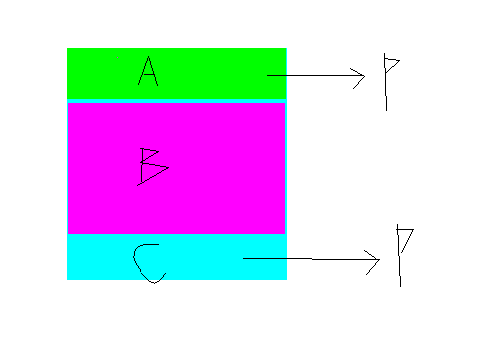
如果A矩形的前缀和MOD K = P， C矩形的前缀和MOD K =Ｐ，说明中间的矩形MOD K= 0； 所以枚举列起点， 终点， 行数， 统计余数出现次数 O(n*M*M);

#include <bits/stdc++.h>
const int M = 405, N = 1e6 + 10;
using namespace std;
#define rt register
int a[M][M], sum[M][M], vis[N], lie[M][M], ret[M];
int main()
{
    //freopen("rally.in", "r", stdin);
    //freopen("rally.out", "w", stdout);
    int n, m, k;
    long long cnt = 0;
    scanf("%d%d%d", &n, &m, &k);
    for(rt int i = 1; i <= n; i++)
        for(rt int j = 1; j <= m; j++){
            scanf("%d", &a[i][j]);
            sum[i][j] = (sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + a[i][j]) % k;
            lie[i][j] = lie[i][j-1] + a[i][j];
        }
        for(int i = 1; i <= m; i++)
            for(int j = i; j <= m; j++){
                for(int p = 1; p <= n; p++){
                    ret[p] = (ret[p-1] + lie[p][j] - lie[p][i-1]) % k;
                    vis[ret[p]] = 0;
                }
                for(int p = 1; p <= n; p++){
                    if(ret[p] == 0) cnt++;
                    cnt += vis[ret[p]];
                    vis[ret[p]]++;
                }
            }
   
    printf("%lld", cnt);
    return 0;
}

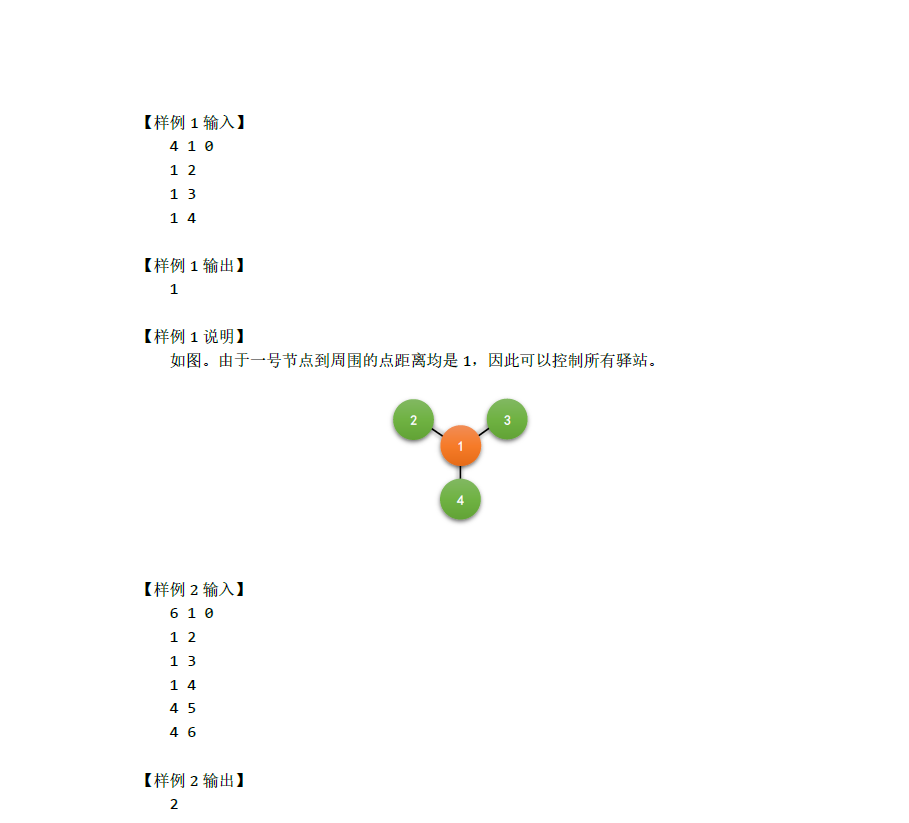
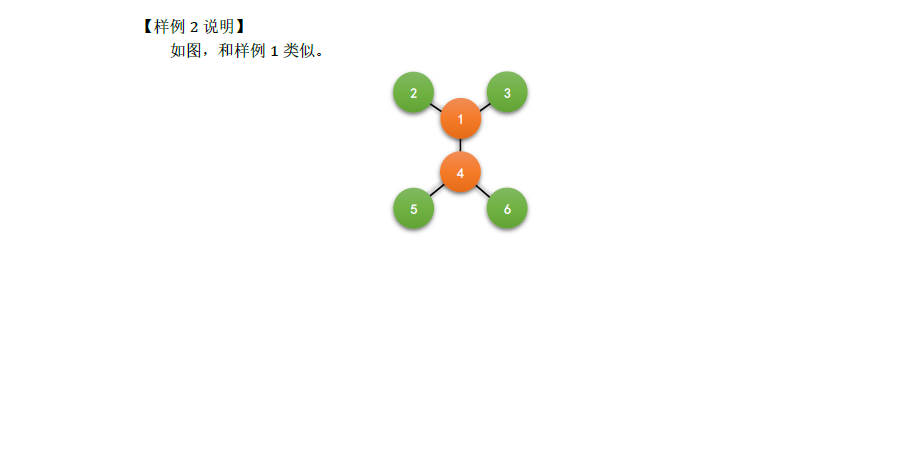
 第二题：

45 分做法  k == 1 dp
dp[u][0] control by son dp[u][1] control by oneself dp[u][2] control by father
dp[u][0] = sum(min(dp[v][0], dp[v][1]) (but there must be at least one dp[v][1])
dp[u][1] = sum(min(dp[v][0/1/2])
dp[u][2] = sum(min(dp[v][0],dp[v][1]))

dp:

void dfs(int u, int f){
    fa[u] = f;
    int delta = inf, sum = 0, child = 0;
    for(int i = h[u]; i; i = G[i].nxt){
        int v = G[i].v;
        if(v == f)continue;
        child++;
        dfs(v, u);
        sum += min(dp[v][1], dp[v][0]);
        delta = min(delta, max(dp[v][0] - dp[v][1], 0));
        if(dp[v][0] < dp[v][1]) pp[u] = 1;
        dp[u][0] += min(dp[v][1], min(dp[v][0], dp[v][2]));
    }
    if(!child){
        dp[u][1] = inf; dp[u][0] = 1;
        return ;
    }
    dp[u][0]++;
    dp[u][1] = dp[u][2] = sum;
    if(!pp[u]) dp[u][1] += delta;
}

AC code 

#include <bits/stdc++.h>
const int M = 1e5 +10;
#define inf 1e8
using namespace std;
int tot, n, k, fa[M], t, dep[M], h[M];
bool vis[M];
struct edge{int v,nxt;}G[M<<1];
void add(int u, int v){G[++tot].nxt = h[u]; h[u] = tot; G[tot].v = v; }
void dfs(int u, int f){
    dep[u] = dep[f] + 1;
    fa[u] = f;
    for(int i = h[u]; i; i = G[i].nxt){
        int v = G[i].v;
        if(v == f)continue;
        dfs(v, u);
    }
}
void dst(int u, int dd, int f){
    vis[u] = 1;
    for(int i = h[u]; i; i = G[i].nxt){
        int v = G[i].v;
        if(v == f)continue;
        if(dd < k)dst(v, dd+1, u);
    }
}
struct Node{
    int id, dep;
    bool operator < (const Node& a)const{
        return a.dep > dep;
    }
};
priority_queue <Node> Q;
int main()
{
    int cnt = 0;
    scanf("%d%d%d", &n, &k, &t);
    for(int i = 1; i < n; i++){
        int u, v;
        scanf("%d%d", &u, &v);
        add(u, v); add(v, u);
    }
    dfs(1, 0);
    for(int i = 1; i <= n; i++)
        Q.push((Node){i, dep[i]});
    for(int i = 1; i <= n; i++){
        int aa = Q.top().id;
        Q.pop();
        if(vis[aa])continue;
        int tt = 0;
        while(tt < k){
            if(!fa[aa])break;
            aa = fa[aa];
            tt++;
        }
        dst(aa, 0, aa);
        //printf("%d ", aa);
        cnt++;
    }
    printf("%d
", cnt);
    return 0;
}

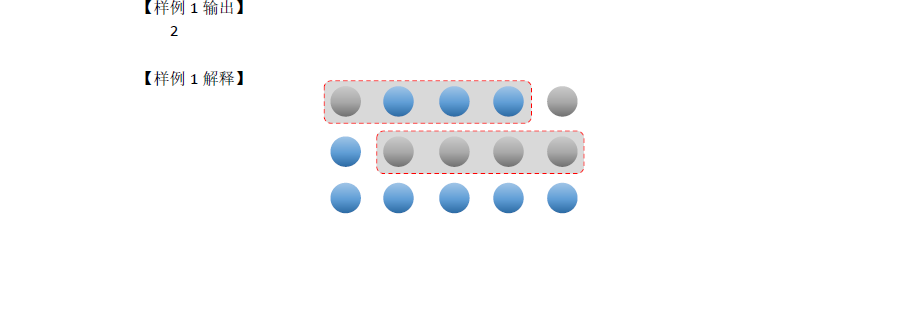
第三题：首先我们发现对于连续的一段灯泡去按它的开关极其费时，因此我们需要一种O（1）复杂度的方法进行开关的操作。

对于序列加减我们可以用差分数组， 对于异或也可以差分；

令差分数组 b[i] = a[i]^a[i+1]  例：

a    1 0 0 0 1

b 1 1 0 0 1 1

将1——5翻转， 则修改B[0] 和 b[5] 就可以了

b 0 1 0 0 1 0

a    0 1 1 1 0

b逆推的a如上； 一个1 会在B中产生至多两个1， 故最多2k个1.，那么原问题被我们玄学的转化为了对于给定的0 1数列，每次对于按要求的某两个数进行取反，问最少次可以使数列全部变为1.

这里有必要提一下原问题麻烦的地方，即对于答案无用的灯泡（亮着的）太多，这样会导致进行大量的无效操作。所以我们只对有1的地方操作,那么他们转化的状态我们就达到某状态的最小操作次数可以预处理出来，最后答案为全0的状态； 这个可以用SPFA跑， 然后由于只有2k个1，我们就可以状压了；

#include<bits/stdc++.h>
using namespace std;
const int N = 1<<18,M = 40005, inf = 1e8;
int a[M], ans, b[M], cnt;
int n, k, m, dis[20][M];
int dp[N];
typedef pair<int, int> pii;
pii p[20];
void bfs(pii st){
    queue <int> q;
    for(int i = 0; i <= n; i++) dis[st.first][i] = inf;
    q.push(st.second);
    dis[st.first][st.second] = 0;
    while(!q.empty()){
        int u = q.front(); q.pop();

        for(int i = 1; i <= m; i++){
            if(u + b[i] <= n && dis[st.first][u] + 1 < dis[st.first][u + b[i]]){
                dis[st.first][u + b[i]] = dis[st.first][u] + 1;
                q.push(u + b[i]);
            }
            if(u - b[i] >= 0 && dis[st.first][u] + 1 < dis[st.first][u - b[i]]){
                dis[st.first][u - b[i]] = dis[st.first][u] + 1;
                q.push(u - b[i]);
            }
        }

    }

}

int solve(int sta){
    //printf("%d
", sta);
    if(dp[sta] != -1)return dp[sta];
    if(sta == 0)return 0;
    dp[sta] = inf;
    int fi = 0;
    while(!((1<<fi)&sta))fi++;
    for(int i = fi+1; i < 2*k; i++)
        if( (1<<i) & sta )
            dp[sta] = min(dp[sta], dis[fi][p[i].second] + solve(sta^(1<<fi)^(1<<i)));
    //printf("%d %d
", sta, dp[sta]);
    return dp[sta];
}

int main(){
    //freopen("starlit.in","r",stdin);
    //freopen("starlit.out","w",stdout);
    scanf("%d%d%d", &n, &k, &m);
    for(int i = 1; i <= k; i++){
        int v;  scanf("%d", &v);
        a[v] = 1;
    }
    for(int i = 1; i <= m; i++)scanf("%d", &b[i]);
    for(int i = 0; i <= n; i++)
        if(a[i] != a[i+1]) p[cnt] = pii(cnt++, i);
    for(int i = 0; i < cnt; i++) bfs(p[i]);
    memset(dp, -1, sizeof(dp));
    int ans = solve((1<<cnt)-1);
    printf("%d",ans);
}