18寒假第六测

第一题：乘法修改的线段树

　　一定不能将change,modify分类讨论定两个标记，会有顺序影响

　　lazy标记一定要long long,又忘了。。。

 代码和上一次差不多

第二题：离散暴力，也可以扫描线

　　离散时要将格子映射成点，不然会出现以下情况：

　　算横着的小矩形宽就是2，算黄色面积宽还是2，因为没有2让3去减

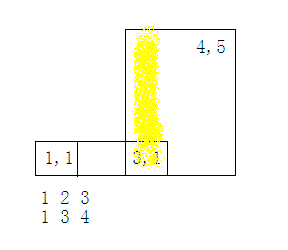
 　　如果映射成点，就像这样，，放图比较好理解，就像扫描线，一个叶子节点存的是一个左闭右开的区间

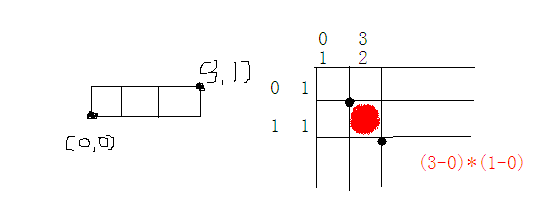
 也可以离散+扫描线，但还没写出来

#include <bits/stdc++.h>

using namespace std;
#define maxn 1005
int disx[maxn*2],disy[maxn*2],xs[maxn*2],xe[maxn*2],ys[maxn*2],ye[maxn*2];
int totx,toty;
bool st[maxn*2][maxn*2];
void read(int &x){
    int f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    x*=f;
}
int main()
{
    freopen("area.in","r",stdin);
    freopen("area.out","w",stdout);
    int n;
    read(n);
    for(int i = 1; i <= n; i++){
        read(xs[i]),read(ys[i]),read(xe[i]),read(ye[i]);
        xs[i]-=1,ys[i]-=1;
        disx[++totx]=xs[i],disx[++totx]=xe[i];
        disy[++toty]=ys[i],disy[++toty]=ye[i];
    }
    sort(disx + 1, disx + 1 + totx);
    sort(disy + 1, disy + 1 + toty);
    totx = unique(disx + 1, disx + 1 + totx) - disx - 1;
    toty = unique(disy + 1, disy + 1 + toty) - disy - 1;
    for(int k = 1; k <= n; k++){
        int xn = lower_bound(disx + 1, disx + 1 + totx, xs[k]) - disx;
        int xm = lower_bound(disx + 1, disx + 1 + totx, xe[k]) - disx;
        int yn = lower_bound(disy + 1, disy + 1 + toty, ys[k]) - disy;
        int ym = lower_bound(disy + 1, disy + 1 + toty, ye[k]) - disy;
        for(int i = xn+1; i <= xm; i++)
        for(int j = yn+1; j <= ym; j++)
            st[i][j] = 1;
    }

    long long ans = 0;
    for(int i = 1; i <= totx; i++)
    for(int j = 1; j <= toty; j++)
        if(st[i][j])
          ans += 1LL * (disx[i] - disx[i - 1]) * (disy[j] - disy[j - 1]);
    printf("%I64d
",ans);
    return 0;
}

第三题：可持久化数组，每次建树logN的空间复杂度，不改变原来的版本

 pool大小为N*2+Q*logN，Q为询问次数

#include <bits/stdc++.h>

using namespace std;
#define maxn 100005
#define ll long long
int a[maxn],n,m,s;
void read(int &x){
    int f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    x*=f;
}

struct Node{
    int v;
    Node *ls, *rs;

}pool[maxn * 32],*tail = pool, *root[maxn];//?

Node * build(int l = 1,int r = n){
    Node *nd = ++tail;
    if(l == r)
        nd->v = a[l];
    else {
        int m = (l + r) >> 1;
        nd->ls = build(l, m);
        nd->rs = build(m + 1, r);
    }
    return nd;
}
#define Ls nd->ls, l, m
#define Rs nd->rs, m+1, r
Node * modify(int delta, int pos, Node *nd, int l = 1, int r = n){
    Node *nnd = ++tail;
    if(l == r) nnd->v = delta;
    else {
        int m = (l + r) >> 1;
        if(pos <= m){
            nnd->rs = nd->rs;
            nnd->ls = modify(delta, pos, Ls);

        }
        if(pos > m){
            nnd->ls = nd->ls;
            nnd->rs = modify(delta, pos, Rs);
        }
    }
    return nnd;
}

int query(int pos, Node *nd, int l = 1, int r = n ){
    if(l == r)
      return nd->v;
    else {
        int m = (l + r) >> 1;
        if(pos <= m)return query(pos, Ls);
        else return query(pos, Rs);
    }
}
Node * print(int pos,Node *nd){
    printf("%d
",query(pos,nd));
    return nd;
}
int main(){
    freopen("array.in","r",stdin);
    freopen("array.out","w",stdout);
    read(n);
    for(int i = 1; i <= n; i++)
        read(a[i]);
    root[0] = build();
    read(m);
    for(int i = 1; i <= m; i++){
        string opt;
        cin>>opt;
        if(opt[0] == 'q'){
            int pos;
            read(pos);
            root[i] = print(pos, root[i - 1]);
        }
        else if(opt[0] == 'm'){
            int pos, x;
            read(pos), read(x);
            root[i] = modify(x,pos,root[i - 1]);

        }
        else {
            int t;
            read(t);
            root[i] = root[t];
        }
    }
}