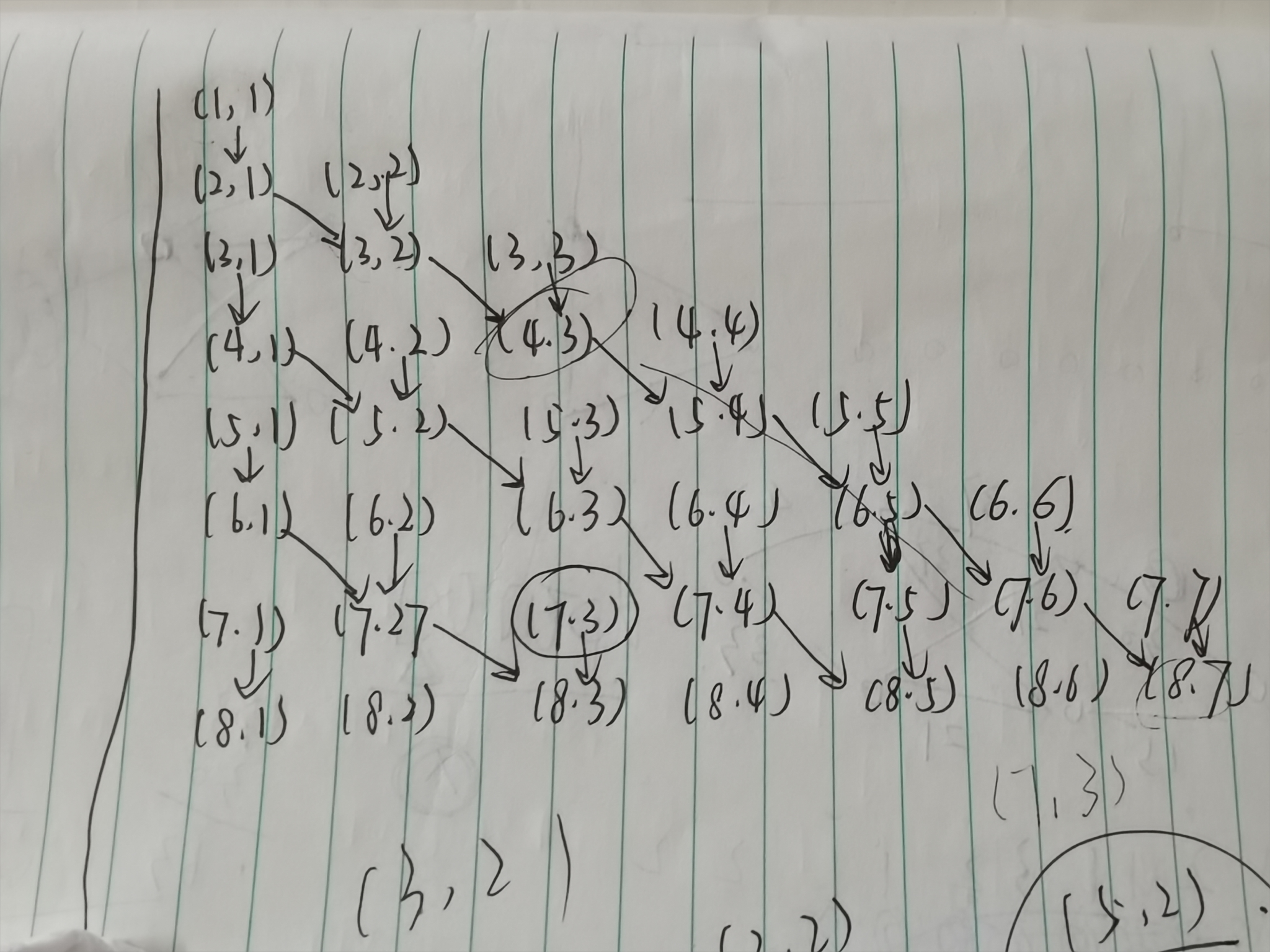F. Triangular Paths 思维

F. Triangular Paths 思维

题目大意：

给你一个由层叠加起来的三角形。

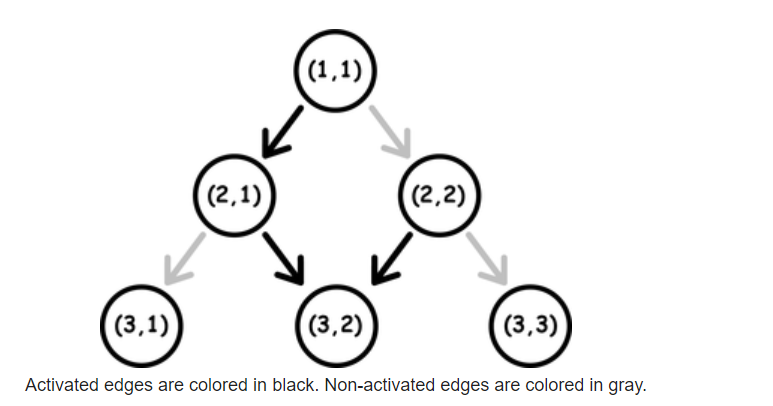
然后对于第 (r) 层，第 (c) 个，如果 ((r+c)) 是一个偶数，那么连向 ((r+1,c)) ，否则连向 ((r+1,c+1))

然后，你可以花费1 的代价改变这个，也就是如果 ((r+1)) 是偶数，你花费钱之后，那么就连向了 ((r+1,c+1)) 而不连向 ((r+1,c)) ，奇数也是一样。

问：你从 ((1,1)) 出发，走过需要你经过的所有的点花费的最小代价是多少。

题目保证：至少存在一条路径可以经过所有的点。

题解：

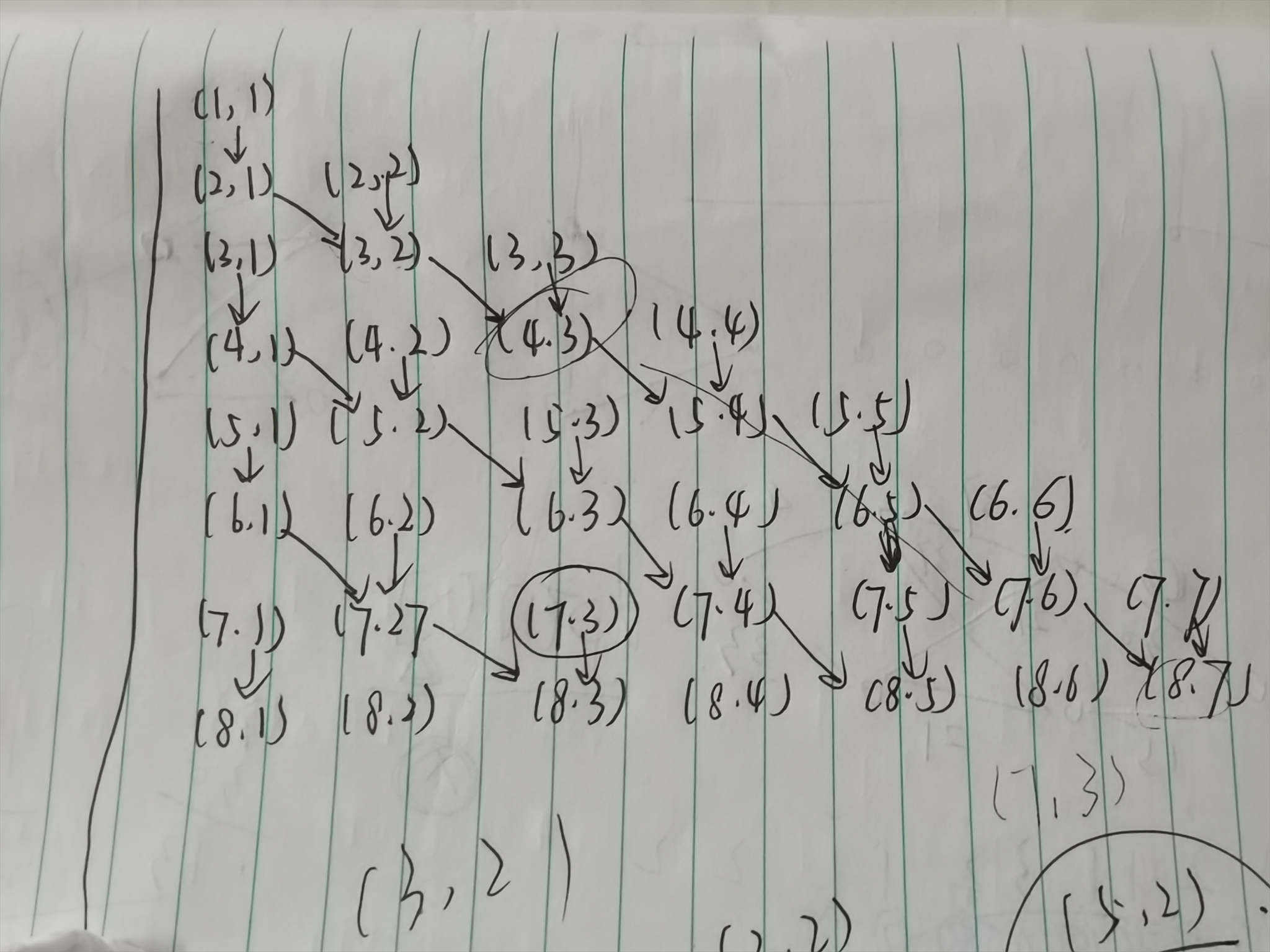
把图化成这个样子更好理解。

• 假设上一个点是 ((sx,sy)) 现在要到达的点是 ((x,y)) 差值是 ((dx,dy))
• 如果 (dx==dy) 并且 ((sx+sy)mod\,2= 0) 那么说明必须更改 (dx) 次
• 如果 (dx==dy) 并且 ((sx+sy)mod\,2=1) 那么是0次
• 否则如果 ((sx+sy)mod\,2=0) 那么就先向下移动一格，然后一直往右下方走，一直到他们的 (y) 相同，然后再判断需要更改的次数
• 另外一个情况则不需要往下移动一格，而是直接往右下方走，直接判断需要更改的次数。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 10;
struct node{
    int r,c;
}e[maxn];
bool cmp(node a,node b) {
    return a.r < b.r;
}
int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        int n;
        scanf("%d", &n);
        for (int i = 1; i <= n; i++) scanf("%d", &e[i].r);
        for (int i = 1; i <= n; i++) scanf("%d", &e[i].c);
        sort(e + 1, e + 1 + n, cmp);
        int sx = 1, sy = 1, ans = 0;
        for (int i = 1; i <= n; i++) {
            int x = e[i].r, y = e[i].c;
            if (sx == x && sy == y) continue;
            int dx = x - sx, dy = y - sy;
            if (dx == dy) {
                if ((sx + sy) % 2 == 0) ans += dx;
            } else {
                if ((sx + sy) % 2 == 0) sx++;
                sx += y - sy, sy = y;
                ans += (x - sx + 1) / 2;
            }
            sx = x,sy = y;
        }
        printf("%d
", ans);
    }
    return 0;
}