没有全部写完,有几题以后再补吧。
第一题:最简单的:飞行员配对方案问题
讲讲这个题目为什么可以用网络流?
因为这个题目是要进行两两之间的匹配,这个就可以想到用二分图匹配,二分图匹配又可以用网络流写。
为什么二分图匹配可以用网络流写呢?
你在二分图上面加一个源点和一个汇点,然后你求从源点到汇点的最大流,这个是不是就是二分图的最大匹配。
第二题:最小路径覆盖问题
这个题目是一个特别明显的二分图问题,也用到了一个比较常见的方法拆点法,
这个再介绍一下拆点法这个网络流里面的基本套路该什么时候用,
如果你碰到一个网络流的题目,题目对每一个点有次数限制,这个时候就需要对这个点进行拆分。
拆分的方法有很多种,这个可以慢慢积累,也没有特别重要。
这个题目如果你对二分图定理很了解,这个就会是一个比较简单的题目了,可以学习一下二分图的定理
主要有三个:最小顶点覆盖数=最大匹配数 最大独立集=总数-最小定点覆盖数 有向无环图(DAG)最小路径覆盖数=原图上的点数-最大匹配数
这几个概念再很多地方都可以看到,尤其是最大独立集。
这个题目就是直接让你求一个图的最小路径覆盖数,这个对每一个点也有次数限制,每个点只能用一次,所以这个就要用拆分法,
不过这个题目所用的拆分法有一点点不同,一般题目都是把一个点拆成两个点,然后把这两个点连起来,连起来的这条直线的容量为1.
但是碰到这个二分图匹配问题,如果你这么连,很显然是没有意义的。
然后再分析:这个最小路径覆盖,最多的肯定是n,一共有n个点,然后我们在合并的过程中路径数量不断减少。
所以这个题目最小路径覆盖数,就是本来有的n个点再减去可以两两合并的数。
最后就是输出,这个输出就自己看代码吧。
第三题:魔术球问题
这个题目也是一个二分图问题,我觉得不是那么简单吧。
给你的柱子数就是最小路径数,放球条件就是建图条件,让你求可以放的最多的球数量,就是最多的点满足可以满足这个图。
这个题目要拆分,一个点连接源点,一个连接汇点,这被拆的两个点不能连起来。
每一个球,就先去遍历,如果可以和之前的一些球有建图条件,就先建图,建完图之后跑最大流(增光路),如果增广路不为0,
那就说明这个可以放在之前用的柱子里面,不然就再开一个柱子,如果柱子数最后达到n,就跳出循环。
这个为什么说增广路不为0,就说明可以放在之前的柱子里面呢?这个是因为,我们对于每一条线得容量都设为1,
所以这个就说明,每新增加一个球,如果增广路不是0,则说明它肯定和之前柱子的最上面的那个球连在了一起。
因为和下面的球就算连在了一起,也没办法增广了(容量为1)
知道了,这些建图就很简单了。这个是一个很巧妙的建图。
可以看下面的图片理解一下。
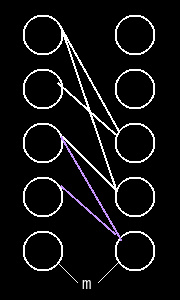
第四题:圆桌问题
这个是一个二分图的多重匹配,这个题目比较简单,这个多种匹配就直接跑一个最大流好了。
题目不是要求同一个单位的人不能坐在一起吗?那就每一个单位都向每一个桌子连一条容量为1的线,这个就可以保证
不会有一个单位的人坐在一起了,如果最大流大于等于所有单位人之和,那就可以满足,否则就不可以。
为什么会这么想呢?这个是因为我首先知道这个是一个网络流的题目,我需要建图,然后就很好做了。
第五题:试题库问题
这个题目就不说了,这个题目和圆桌问题简直一模一样。
第六题:最长不下降子序列
这个题目建图很难想,第一问就是一个裸的LIS,
主要就是第二问,这个题目我是没有想到,看了一下题解,首先要进行拆点,因为每一个点只能用一次。
这个建图就是先对这个序列进行处理,怎么处理呢?求出f数组,f[i]代表到第i位的最长不下降子序列,
如果f[i]==1,那就直接和源点相连,然后之后如果满足a[i]>=a[j]&&i>j&&f[i]==f[j]+1
那么就把j的出点和i的入点连起来。
这个就是建图,这个样子建图好难想啊。
不过看了题解之后也没有觉得特别难了,这个更加具体的解析就看看博客吧。
第七题:餐巾计划问题
这个题目的建图很难想,一般就看看题目然后就看题解了。
这个是把每一天拆成了两个点,一个上午点和一个下午点。
下午点都和源点相连表示一天的结束,上午点和汇点相连,表示需要的餐巾数量。
与源点和汇点相连的点的cap都设置成这一天需要的餐巾数量,这个来限制送去快洗和慢洗的毛巾数。
然后再去处理3+1,3表示快洗,慢洗,新买,1表示不洗。因为之前以及被限制过了,
所以这里的不需要再去考虑有多少脏毛巾,这里的cap应该设置成inf,因为一次可以洗无数条毛巾。
这个不洗的要好好处理,这个不洗表示直接积累到下一天,那么就说明,这个的cost=0,
但是我们会疑惑,如果这样会不会影响到网络流? 其实这个不会,因为餐巾的积累会往下一天的晚上传递,意思
是说,这个餐巾不会算作这一天需要的餐巾数,但是那为什么还要连边呢?这个连边会让它往下一天传递,
那么餐巾积累,之后可以考虑一起洗掉。一起洗一堆和一次洗一条所用的时间是一样的,
所以如果我们之后再堆在一起洗也许会更优。
这个题目,第一个是要用到拆点把一天拆成上午和下午,第二个是转移,不洗就之间向下一天转移费用为0,买新的就从源点向这一天的上午
直接相连费用为新毛巾的费用,快洗就把这一天向洗好的早上相连,费用为快洗的费用,慢洗同理。
第八题:P2770 航空路线问题
这个也是一个费用流的问题,这个知识把求最小费用改成求最大费用,这个改法有两种,一种就是把d改成-inf or 0xef
然后就是一个模板题了。
输出需要注意
第九题:数字梯形问题
第一问:这一问要进行拆点和边权限制,用拆点来保证每一个数字只被经过一次
第二问:这一问就不需要拆点了,只需要边权限制
第三位:这一问没有任何限制,就是源点和第一行的数字相连容量为1 .
第十题:运输问题
这个也是一个裸的最大费用最大流和最小费用最大流的问题
第十一题:P4014 分配问题
同上
第十二题:负载平衡
这个题目应该也是把仓库进行拆点,因为这个仓库是环状摆放,并且只能向两边进行转移,
所以就把每一个仓库进行拆点,入点和源点相连,容量为这个仓库货物数量,费用为0,然后每一个仓库入点和左右的仓库的出点相连。
费用为1,然后每一个仓库的出点和汇点相连,所以最后的最小费用就是搬运量。
第十三题:深海机器人
这个题目通过数据范围判断出这个是一个网络流,
建图就是每一个位置的机器人可以走到的下一个位置。因为这个直接给的就是路径的权值不是点的权值,所以就不需要进行拆分。
第十四题:火星探险问题
这个题目和上面是一样的,只不过给的是点的权值,所以需要进行拆分。
第十五题:最长k可重区间集问题
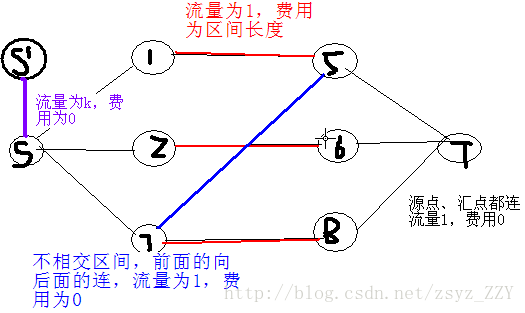
这个题目的建图很巧妙,我也讲不清楚。
第十六题:最长k可重线段集问题
这个题目和上面那个是一样的,只不过可能有就是平行于y轴的直线,这个需要处理一下,这个也是要连的。