计算几何进阶

带家好，今天我们来聊聊计算几何。上接前传：计算几何基础。

早在 2021 年 6 月我就产生了学习计算几何的欲望，并也对一些基本的计算几何算法进行了相应的学习。可惜那时候介于水平原因没有学透，NOIp 后本来打算补一补的也给鸽掉了，一推就到了现在，觉得不能再鸽了就在过年期间抽空学掉了 /菜汪。

废话少说，让我们开始吧！

凸包

zszz，凸包分为两种，直线凸包和点凸包。计算几何当中的凸包多为点凸包，即给定平面上若干个点所形成的凸包，而直线凸包则常用于斜率优化与李超线段树中，因此下文中我们将着重讨论点凸包的建法。

Graham 算法

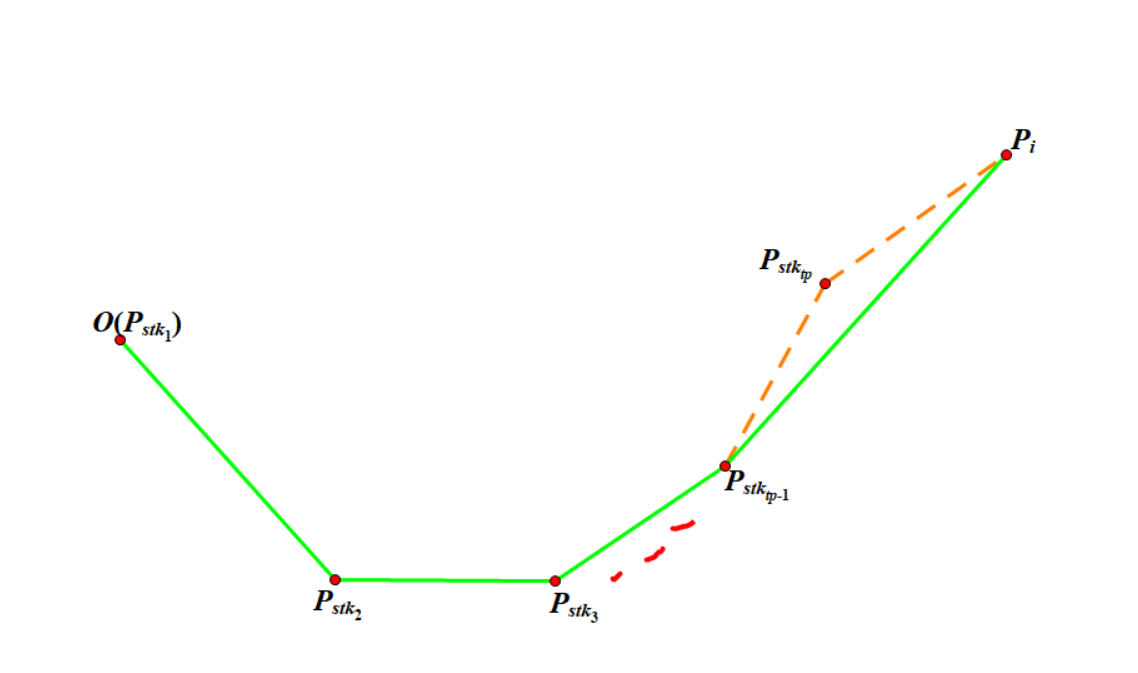
Graham 算法的核心思想是，先找到凸包上的一个点（一般取按横坐标为第一关键字、纵坐标为第二关键字升序排序后的第一个点）\(O\) 为原点，将其余点 \(P_i\) 按 \(\vec{OP_i}\) 的辐角排序。并按逆时针（即辐角从小到大）的顺序考虑所有点并动态维护一个栈，存储当前所有在凸壳中的点的编号，每次加入一个点 \(P_i\) 时，如果出现如下图所示的情况（即 \(\vec{P_{stk[tp]}P_{stk[tp-1]}}\times\vec{P_{stk[tp]}P_i}\ge 0\)）就弹出栈顶元素，如此重复下去直到 \(\vec{P_{stk[tp]}P_{stk[tp-1]}}\times\vec{P_{stk[tp]}P_i}\lt 0\) 为止。

用 graham 实现的模板题代码：

const int MAXN = 1e5;
int n;
struct point {
	double x, y;
	point() {x = y = 0;}
	point(double _x, double _y) {x = _x; y = _y;}
	point operator + (const point &rhs) const {return point(x + rhs.x, y + rhs.y);}
	point operator - (const point &rhs) const {return point(x - rhs.x, y - rhs.y);}
	point operator * (const double &rhs) const {return point(x * rhs, y * rhs);}
	point operator / (const double &rhs) const {return point(x / rhs, y / rhs);}
	double operator | (const point &rhs) const {return x * rhs.y - y * rhs.x;}
	double operator ^ (const point &rhs) const {return x * rhs.x + y * rhs.y;}
	double operator ~ () const {return sqrt(x * x + y * y);}
	double operator ! () const {return atan2(y, x);}
} p[MAXN + 5], ori;
int stk[MAXN + 5], tp = 0;
bool cmp(point a, point b) {
	if ((!(a - ori)) != (!(b - ori))) return !(a - ori) < !(b - ori);
	if (a.x != b.x) return a.x < b.x;
	return a.y < b.y;
}
int main() {
	scanf("%d", &n); int id = 1;
	for (int i = 1; i <= n; i++) scanf("%lf%lf", &p[i].x, &p[i].y);
	for (int i = 2; i <= n; i++) if (p[i].x < p[id].x || (p[i].x == p[id].x && p[i].y < p[id].y)) id = i;
	swap(p[1], p[id]); ori = p[1]; sort(p + 2, p + n + 1, cmp); stk[++tp] = 1;
	for (int i = 2; i <= n; i++) {
		while(tp >= 2 && ((p[stk[tp - 1]] - p[stk[tp]]) | (p[i] - p[stk[tp]])) >= 0) tp--;
		stk[++tp] = i;
	}
	double ans = 0;
	for (int i = 1; i < tp; i++) ans += (~(p[stk[i]] - p[stk[i + 1]]));
	ans += (~(p[stk[tp]] - p[stk[1]]));
	printf("%.2lf\n",ans);
	return 0;
}

Andrew 算法

相较于 graham 算法，个人则更经常使用 andrew 算法求解点凸包。

和 graham 一样，我们还是将所有点按横坐标第一关键字，纵坐标第二关键字的顺序升序排序，那么显然，第 \(1\) 个点和第 \(n\) 个点肯定是在凸包中的，而中间在凸包上的部分肯定是一段上凸壳和一段下凸壳，故我们可以直接从左到右求一遍上凸壳和下凸壳，然后把这些点按照顺序拼接起来就是整个凸包。那么怎么求上 / 下凸壳呢，方法和 graham 算法差不多，以下凸壳为里，还是每加入一个点都判一下凸包最后两个点所形成的向量 与 凸包最后一个点与新加入的点形成的向量 的叉积，不断弹出栈顶直到这个叉积 \(<0\) 为止。

上述两个算法的时间复杂度均为 \(n\log n\)​。

const int MAXN = 1e5;
int n;
struct point {
	double x, y;
	point() {x = y = 0;}
	point(double _x, double _y) {x = _x; y = _y;}
	point operator + (const point &rhs) const {return point(x + rhs.x, y + rhs.y);}
	point operator - (const point &rhs) const {return point(x - rhs.x, y - rhs.y);}
	point operator * (const double &rhs) const {return point(x * rhs, y * rhs);}
	point operator / (const double &rhs) const {return point(x / rhs, y / rhs);}
	double operator | (const point &rhs) const {return x * rhs.y - y * rhs.x;}
	double operator ^ (const point &rhs) const {return x * rhs.x + y * rhs.y;}
	double operator ~ () const {return sqrt(x * x + y * y);}
	double operator ! () const {return atan2(y, x);}
} p[MAXN + 5], ori;
int stk[MAXN + 5], tp = 0;
bool cmp(point a, point b) {return (a.x < b.x || (a.x == b.x && a.y < b.y));}
int main() {
	scanf("%d", &n); double ans = 0;
	for (int i = 1; i <= n; i++) scanf("%lf%lf", &p[i].x, &p[i].y);
	sort(p + 1, p + n + 1, cmp); stk[++tp] = 1;
	for (int i = 2; i <= n; i++) {
		while (tp >= 2 && ((p[i] - p[stk[tp]]) | (p[stk[tp - 1]] - p[stk[tp]])) >= 0) tp--;
		stk[++tp] = i;
	}
	for (int i = 1; i < tp; i++) ans += (~(p[stk[i]] - p[stk[i + 1]]));
	stk[tp = 1] = n;
	for (int i = n - 1; i; i--) {
		while (tp >= 2 && ((p[i] - p[stk[tp]]) | (p[stk[tp - 1]] - p[stk[tp]])) >= 0) tp--;
		stk[++tp] = i;
	}
	for (int i = 1; i < tp; i++) ans += (~(p[stk[i]] - p[stk[i + 1]]));
	printf("%.2lf\n",ans);
	return 0;
}

旋转卡壳

旋（xuan4）转（zhuan4）卡（ka3）壳（qiao4）（bushi）。

一个和凸包关系非常大的 trick，常用于在枚举凸包上某个点 / 线段过程中找凸包上与其最远的点 / 线段，最经典的应用便是平面最远点对。很显然，平面最远点对的两个端点都在凸包上，因此考虑枚举一个端点 \(P_i\)​​，那么显然 \(\triangle P_iP_{i+1}P_j\)​​ 的面积关于 \(j\)​​ 是单峰的（其中 \(P_{n+1}=P_1\)​​），我们称使 \(\triangle P_iP_{i+1}P_j\)​​ 最大的点 \(j\) 为 \(P_iP_{i+1}\) 的对踵点，那么我们可以在枚举 \(i\) 的过程中 two pointers 维护 \(i\) 的对踵点 \(j\)，然后用 \(P_j,P_{j-1},P_{j+1}\) 与 \(P_i\) 的距离更新答案即可。注意，这里 two pointers 的依据应是 \(\triangle P_iP_{i+1}P_j\) 与 \(\triangle P_iP_{i+1}P_{j+1}\) 的面积关系，而不是 \(P_iP_j\) 与 \(P_iP_{j+1}\)​​ 的长度关系。具体 hack 见 https://wuhongxun.blog.uoj.ac/blog/3679 的 T3 子任务 6。

一些例题

7. P2116 城墙

根据凸多边形外角和 \(2\pi\)​ 可知曲线部分长度就是 \(2\pi L\)​，而直线部分显然就是凸包周长，直接求即可。就当练练手吧。

8. P4166 [SCOI2007]最大土地面积

首先还是建出凸包，对凸包大小分情况讨论：

• 如果凸包大小 \(\le 2\)，那么显然所有点都在一条直线上，答案为 \(0\)。
• 如果凸包大小 \(=3\)，那么根据调整法，最优四边形的四个顶点中有三个都在凸包上，也就是说这个四边形肯定是凹四边形，因此我们假设凸包上的三个点为 \(A,B,C\)，我们枚举第四个点 \(P_i\)，那么以 \(A,B,C,P_i\) 为顶点的四边形面积的最大值就是 \(S_{\triangle ABC}-\min\{S_{\triangle ABP_i},S_{\triangle ACP_i},S_{\triangle BCP_i}\}\)，对所有可能的 \(P_i\) 取个 \(\max\) 即可得到答案。
• 如果凸包大小 \(=4\)，那么显然此时最优四边形的四个顶点都在凸包上，我们考虑枚举四边形中相对的顶点 \(A,C\)，那么我们考虑直线 \(AC\) 将凸包分成的两个部分，显然 \(B,D\) 分别为两个部分中，使得三角形 \(ACP\) 面积最大的顶点 \(P\)，这个可以旋转卡壳轻松求出。

时间复杂度 \(n^2\)。

9. CF682E Alyona and Triangles

结论题一道。

结论：找出这 \(n\) 个点中每三个点组成的三角形中，面积最大的三角形 \(ABC\)，再找出以 \(\triangle ABC\) 为中位线三角形的三角形 \(\triangle DEF\)，那么 \(\triangle DEF\) 符合条件。\(\triangle ABC\) 可以通过枚举两个顶点 + 旋转卡壳求出。时间复杂度 \(n^2\)。

证明：考虑直线 \(DE,DF,EF\)，显然对于不在 \(\triangle DEF\) 中的点，其至少在这三条直线中的某一条的另一侧，不妨假设其在 \(DE\) 的另一侧，那么显然这个点到 \(AB\) 距离 \(>\) \(C\) 到 \(AB\) 的距离，这样就会出现比 \(\triangle ABC\) 面积更大的三角形 \(\triangle ABP\)​。

时间复杂度 \(n^2\)。

10. CF1142C U2

考虑将所有点 \((x,y)\) 变为 \((x,y-x^2)\)，那么答案就是上凸壳上的点数 \(-1\)，直接用维护凸包的方式维护即可。

11. P3187 [HNOI2007]最小矩形覆盖

首先，在矩形的四条边中，必然有一条边的一个部分与凸包上的一条边重合。否则我们肯定可以将矩形旋转一个角度使得面积不减。

那么我们就在凸包上枚举这条与矩形的边重合的边 \(P_iP_{i+1}\)​，那么显然矩形中，与这条边相对的边必然经过 \(P_iP_{i+1}\)​ 的对踵点，这个可以 two pointers 求出。

这样一来我们就确定了两条边的位置了，考虑如何进一步确定与 \(P_iP_{i+1}\) 垂直的两条边的位置，显然这两条边必须卡住凸包上最左端和最右端的点，因此我们只用知道凸包上相对于 \(P_iP_{i+1}\) 来说，最靠左和最靠右的点，这个同样可以 two pointers 维护，具体来说我们假设动态维护最左端的点 \(P_k\)，当 \(k\) 变为 \(k+1\) 时，我们分别过 \(P_k,P_{k+1}\) 做 \(P_iP_{i+1}\) 的垂线，然后根据垂足与 \(P_i\) 的距离即可判定 \(P_{k+1}\) 是否相较于 \(P_k\) 更靠左。

细节有点多，不过相较于校内模拟赛中某些题，还是要良心不少的。

12. CF1045E Ancient civilizations

凸包与构造结合的好题。

首先建出凸包，如果凸包上黑白色的段数 \(\ge 2\)，那么显然不可能将黑点、白点都连成一棵生成树，直接输出 Impossible 即可。

那么可以证明，对于剩余情况，必然存在合法的连边方案。在探究具体如何处理剩余情况之前，我们先来讨论一些特殊情况，进而将其推广到一般情况：

• 凸包上只有三个点，并且所有点（包括凸包上的点）颜色都一样。

  这时候我们先将凸包连成一条链，随便找到中间一个点并随便将其与凸包上某个点连边，然后将整个三角形分成三个小三角形递归处理即可。容易证明其正确性。

• 凸包上只有三个点，并且恰有两个点颜色相同。

  不妨假设凸包上有两个黑点 \(A,B\) 和一个白点 \(C\)，那么我们先在 \(A,B\) 间连边，考虑凸包内部的点，如果存在至少一个白点，那么我们就取出这个白点 \(D\)，然后连边 \(CD\)，并将其余点分到 \(\triangle ABD,\triangle ACD,\triangle BCD\) 中处理即可。否则我们任取一个黑点 \(D\)，连边 \(AD\)（或 \(BD\)），然后还是递归三个三角形即可。值得注意的是，当三角形内部既有黑点又有白点时，不能随便取一个点而必须强调“取一个白点”，因为如果取到的是黑点 \(D\)，并且三角形 \(ABD\) 中有白点 \(E\)，那么 \(C,E\) 将不能连通。

• 凸包上只有三个点。

  • 如果所有点的颜色都相同，那么按照上面第一种情况处理即可。

  • 如果凸包上恰有两个点颜色相同，那么按照上面第二种情况处理即可。

  • 否则，凸包上三个点颜色相同，但凸包内部有颜色不同于凸包上三个点的点，我们找出这样的点 \(D\)，假设凸包上的点为 \(A,B,C\)，那么我们按照“凸包上只有三个点”的情况处理三个三角形 \(\triangle ABD,\triangle ACD,\triangle BCD\) 即可。

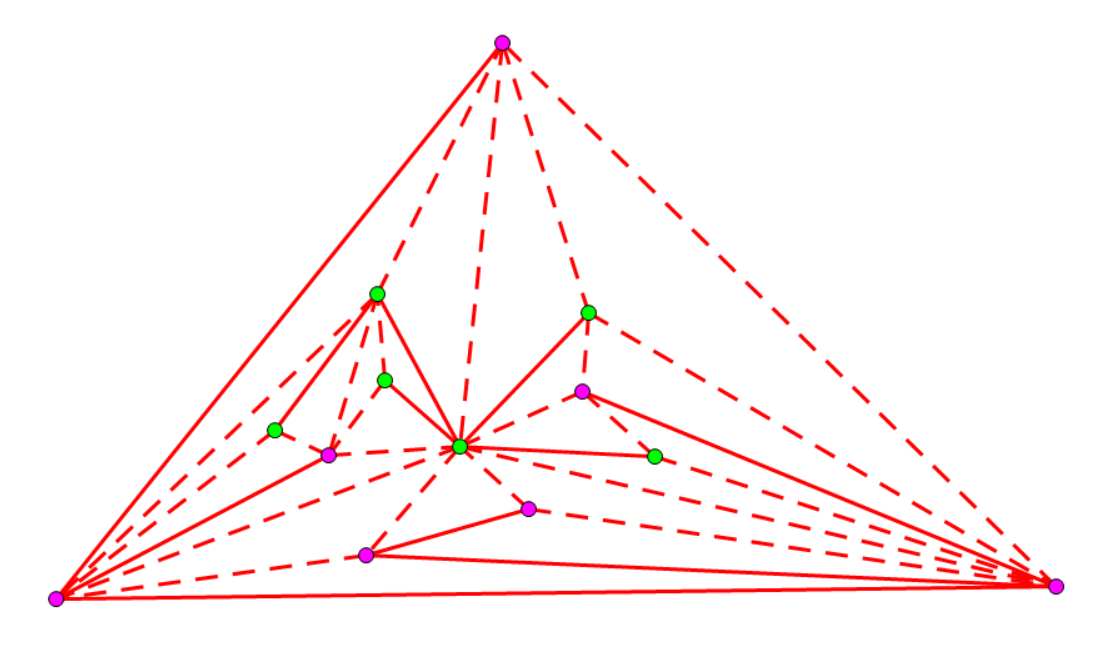
  下图是上面的算法流程的一个例子（其中实线表示连出的边，虚线表示三角剖分连出的线，粉点、绿点表示两种颜色）：

  

  去掉虚线以后：

  

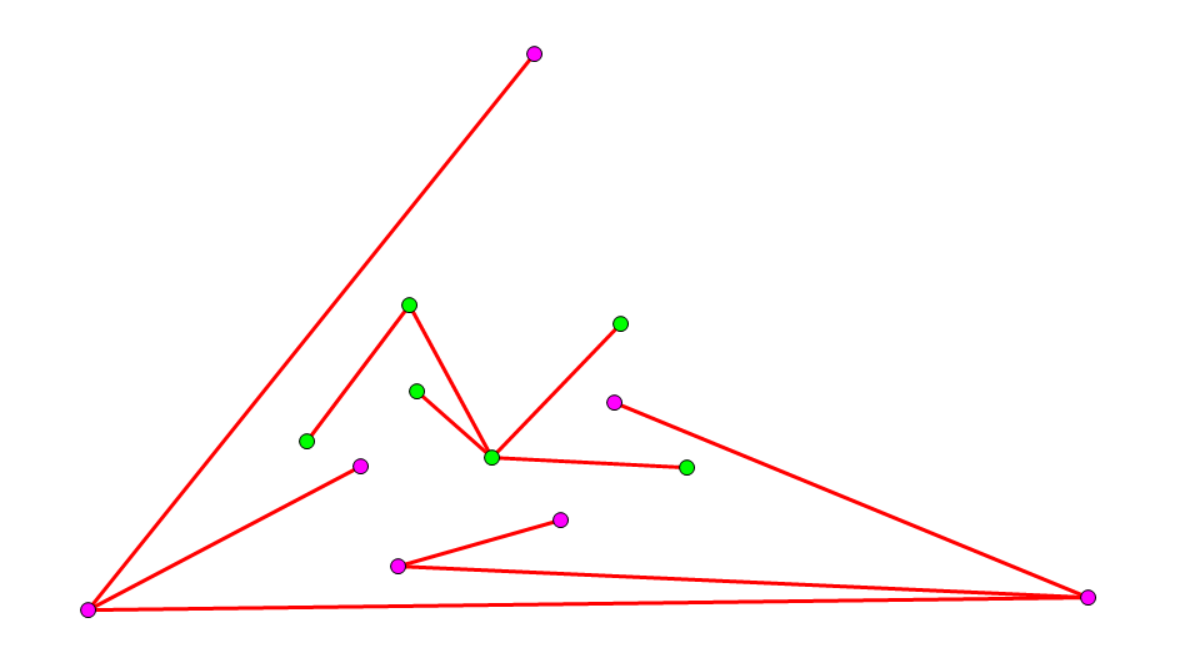
接下来考虑原题：

• 如果所有点颜色都一样，那么我们将其三角剖分成若干个三角形，然后对每个三角形分别进行上面的情况三即可。
• 如果凸包上所有点颜色都一样，但内部存在异色点，我们任取一异色点，将其与凸包所有顶点相连形成 \(n\) 个三角形，对每个三角形分别进行上面的情况二即可。
• 否则如果凸包上恰有一个点与其他点颜色不同，那么假设这个点为白色，其他点为黑色，我们就在凸包内部找一个白点然后将这个点与凸包顶点连边形成 \(n\) 个三角形分别处理，如果凸包内部没有白点就改找一个黑点即可。
• 否则，假设凸包上 \(P_1\sim P_k\) 为黑色，\(P_{k+1}\sim P_m\) 为白色，我们就将这个三角形剖成 \(P_1P_2\cdots P_kP_{k+1}\) 和 \(P_{k+1}P_{k+2}\cdots P_{m-1}P_m\) 两个多边形——显然这两个多边形上都恰有一个点与其他点颜色不同，分别处理这两个多边形即可。

时间复杂度 \(n^2\)。

凸包的闵可夫斯基和

考虑两个凸包 \(A,B\)，定义它们的闵可夫斯基和为一个区域 \(C=\{a+b|a\in A,b\in B\}\)。

那么我们感性地理解一下，\(C\) 也是一个凸包。更一般地，我们考虑取出 \(A,B\) 中最左下角（按横坐标第一关键字、纵坐标第二关键字升序排序后的第一位）的点 \(P,Q\)，那么显然 \(P+Q\) 为 \(C\) 的一个顶点，我们从 \(P\) 开始，逆时针遍历一遍凸包 \(A\) 并将经过的向量储存下来，同理按照同样方式遍历一遍凸包 \(B\)，那么我们将所有向量极角排序并从 \(P+Q\) 开始按顺序加入所有向量，这样画出的图形是一个凸包，这样我们就得到了两个凸包的闵可夫斯基和。

可以通过归并排序做到 \(\mathcal O(|A|+|B|)\) 的复杂度。

一个小注意点：如果直接按照上面的方式归并排序建出闵可夫斯基和之后，可能会出现三点共线的情况，因此这里有两种处理方法，一是在求凸包时特殊处理一下这条线段与凸包上一条线段极角相同的情况。二是求出闵可夫斯基和之后再将得到的点集扔回去求一遍点凸包。

一些例题

13. P4557 [JSOI2018]战争

模板题，求出 \(A\) 与 \(-B\) 的闵可夫斯基和以后对每组询问判断一下点是否在多边形内部即可，判断点在多边形内部可以二分。

14. P8101 [USACO22JAN] Multiple Choice Test P

重要观察：最终答案所对应的点一定是 \(n\) 个凸包的闵可夫斯基和的一个顶点。

因此直接分治求闵可夫斯基和即可，时间复杂度 \(n\log n\)。

15. CF1195F Geometers Anonymous Club

容易发现，两个凸包 \(A,B\) 的闵可夫斯基和的顶点数就是 \(A,B\) 按逆时针方向旋转一周经过的线段的不同极角个数，因此问题类似于区间数颜色，直接无脑莫队硬上即可。

注意，莫队是均摊数据结构，因此直接按多边形下标左右端点分块复杂度实际上是假的，正确的姿势是，对多边形大小做一遍前缀和 \(sum\)，然后对于询问 \([l,r]\)，视作区间 \([sum_{l-1}+1,sum_r]\) 然后再莫队（不过这题好像直接对多边形下标分块也能过？就离谱）

平面最近点对

一个比较杂的知识点，不过也顺带着一起讲了吧（

在学习 KDT 时我们已经学习了如何使用 KDT 解决这个问题，接下来我们要学习用计算几何的方法以更优秀的复杂度解决它（

先将所有点按横坐标排序。考虑分治，分治到区间 \([l,r]\)​ 时，记 \(mid=\lfloor\dfrac{l+r}{2}\rfloor\)​，那么我们先分治 \([l,mid],[mid+1,r]\)（为什么要强调先后关系呢？我相信聪明的读者看到后面一定就会懂了）。考虑用 \(X\in[l,mid],Y\in[mid+1,r]\) 中的点对 \((X,Y)\) 更新答案。直接更新显然会爆炸，考虑优化，我们记当前答案为 \(ans\)，那么显然横坐标距离 \(x_{mid}\) 超过 \(ans\) 的点一定是没用的，再其次，我们如果将 \([l,r]\) 中所有点按 \(y\) 坐标排序，那么对于一个点 \(p\)，可能与 \(p\) 形成对答案产生影响的点对的点 \(q\) 的纵坐标一定是一段区间，因此我们考虑一个非常暴力的思想：枚举到一个 \(x_p\) 时，暴力向后枚举 \(q\) 直到它们纵坐标差 \(>ans\) 即可——当然这里枚举的 \(p,q\) 离 \(x_{mid}\) 的距离不能超过答案，否则这样的点一定不会对答案产生贡献。

令我们又惊又喜的是，加上这么一个不起眼的优化后，复杂度就变成 cdq 分治的复杂度 \(n\log^2n\) 了，使用归并排序代替 sort 甚至可以实现 \(n\log n\)，考虑证明，我们假设当前枚举到点 \(p\)，那么我们以 \(p\) 为圆心，\(ans\) 为半径做圆，再做以 \(p\) 为中心，边长为 \(2ans\) 的正方形，那么显然我们枚举到的点都位于这个正方形中，否则选择其作为一个端点 \(\in[l,mid]\)，另一个端点 \(\in[mid+1,r]\)​ 的点对的两个点之一一定不优，而我们枚举到的点又必然不会位于圆内——否则我们在分治 \([l,mid],[mid+1,r]\) 时 \(ans\) 一定会变得更小（这也就是为什么前面要强调先后关系），也就是说可能被枚举到的点只能位于四个角上，而显然不可能存在某个角上有多于两个点，因此我们最多枚举到 \(4\) 个点，是常数级别的，证毕。

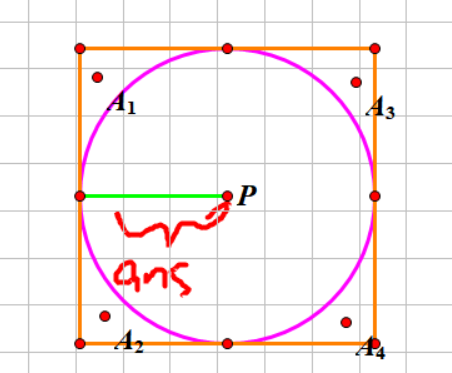
比较可惜，这个做法比较难扩展到 \(k\)​ 维空间最近点对中，如果硬要扩展的话，复杂度可能是 \(n\log^{k-1}·2^k\)​，可能有复杂度更优的做法 / 乱搞做法，也欢迎强大的读者们思考以后在评论区留言。

代码：

const int MAXN = 4e5;
const ll INF = 9e18;
int n; ll res = INF;
struct point {int x, y;} p[MAXN + 5];
ll dis(point A, point B) {return 1ll * (B.x - A.x) * (B.x - A.x) + 1ll * (B.y - A.y) * (B.y - A.y);}
bool cmpx(point A, point B) {return A.x < B.x;}
bool cmpy(point A, point B) {return A.y < B.y;}
void solve(int l, int r) {
	if (l == r) return; int mid = l + r >> 1, xmid = p[mid].x;
	solve(l, mid); solve(mid + 1, r);
	static point pp[MAXN + 5], tmp[MAXN + 5]; int cc = 0, p1 = l, p2 = mid + 1, p3 = l - 1;
	while (p1 <= mid && p2 <= r) {
		if (p[p1].y < p[p2].y) tmp[++p3] = p[p1++];
		else tmp[++p3] = p[p2++];
	}
	while (p1 <= mid) tmp[++p3] = p[p1++];
	while (p2 <= r) tmp[++p3] = p[p2++];
	for (int i = l; i <= r; i++) p[i] = tmp[i];
	for (int i = l; i <= r; i++) if (1ll * (p[i].x - xmid) * (p[i].x - xmid) < res)
		pp[++cc] = p[i];
	for (int i = 1; i <= cc; i++) for (int j = i + 1; j <= cc; j++) {
		if (1ll * (pp[i].y - pp[j].y) * (pp[i].y - pp[j].y) > res) break;
		chkmin(res, dis(pp[i], pp[j]));
	}
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d%d", &p[i].x, &p[i].y);
	sort(p + 1, p + n + 1, cmpx); solve(1, n);
	printf("%lld\n", res);
	return 0;
}

一些杂题

16. CF598F Cut Length

巨大阿巴细节题。

首先乍一眼此题的做法十分显然：暴力求出直线与多边形每条边的交点，并将这些交点按横坐标第一关键字、纵坐标第二关键字排序，这样用射线法可以知道每一段是否在多边形内部。

然后一写……WA？仔细一看发现我们没有正确处理直线与一条边重合 / 一个点的情况。稍微分析一下可以发现，直线与多边形交于一个点有两种可能，要么穿过这个点进入多边形内部，要么经过这个点与多边形擦边而过，那么我们怎么区分这两种情况呢？首先我们先假设多边形没有 \(180\) 度的内角——如果有我们就可以将与这个角相邻的两条边视作一条，\(\mathcal O(n)/\mathcal O(n^2)\) 预处理一下即可。我们假设这条线与多边形交于某个点 \(P_i\)，那么容易发现，如果 \(P_{i-1},P_{i+1}\) 在直线的同一侧，那么这条线与 \(P_i\) 属于擦边而过的情况，这个交点应当算两遍，否则这条直线是穿过这个交点进入多边形的。对于多边形某条边与直线的某一部分完全重合的情况也是如此，假设多边形的边 \(P_iP_{i+1}\) 完全位于多边形中，那么同样地也有两种可能：\(P_{i-1},P_{i+2}\) 位于直线的同一侧，此时这条直线相当于是在 \(P_iP_{i+1}\) 处与多边形打了个擦边球，没有通过这条边进入多边形；\(P_{i-1},P_{i+2}\) 位于直线的异侧，此时这条直线先是擦过了这条边，然后顺着这条边进入了多边形。

当然还有很多很多细节，具体实现可见 https://codeforces.com/contest/598/submission/145372382

17. P4518 [JSOI2018]绝地反击

首先一眼二分答案。

考虑如何判定一个半径 \(r\) 是否可行：考虑以每个点为圆心，\(r\) 为半径做圆。设以原点为圆心，\(R\) 为半径的圆为 \(\omega\)，那么对于一个以给定的点为圆心的圆 \(\omega'\)，其与 \(\omega\) 的关系有以下三种可能：

• 相离（或者圆 \(\omega\) 完全包含圆 \(\omega'\)），如果出现此种情况说明存在某个坐标不能在 \(r\) 的时间内到达圆上，直接返回无解。
• \(\omega’\) 完全包含 \(\omega\)，如果出现此种情况说明该点可以在 \(r\) 的时间内到达圆上任意一点。
• 相交。

对于第三种情况，我们记这些圆与 \(\omega\) 的交点集合为 \(S\)，那么根据直觉，如果 \(r\) 可行，那么必然存在一种合法的方案，使得最终 \(n\) 艘飞船所对应的 \(n\) 个点中，必然存在至少一艘飞船所对于的点属于 \(S\)，因此问题转化为，有 \(|S|\) 种候选方案，你需要对每种候选方案判定其是否可行。这是一个经典的二分图匹配问题，在能够匹配的点之间连边，然后判定得到的二分图是否存在完美匹配即可。

直接做复杂度大概是 \(n^{3.5}\log V\) 的，无法通过，考虑优化，注意到每艘飞船能够匹配的点是环上的一段区间，因此考虑 Hall 定理，根据经典结论，对于“二分图中，一个左部点能够匹配的右部点集是一段区间”的模型，我们只用对每个右部点的区间 \([l,r]\)，检验左部点中，连边范围与 \([l,r]\) 有交的点数是否 \(\ge r-l+1\)​ 即可。对于环的情况也不例外，只要对每个环上的区间检验即可。直接做复杂度是 \(n^4\log V\) 的，可以使用扫描线将其优化到 \(n^2\log n\log V\)。