0-1背包
- 描述:N件物品,第i件的重量是w[i],价值v[i]。有一个容量为W的背包,求将哪些物品放入背包可使总价值最大。每件物品可以用0或1次。
- 分析:根据题意,可以写出表达式:
最直接的思路就是:对于每件物品,都有yes/no两种选择,尝试所有的组合,记录每个组合的价值,选出满足重量条件的最大价值。时间复杂度(O(2^n)),空间复杂度(O(n))。
// backtracking
class knapsack01 {
public:
int knapsack(int W, vector<int>& w, vector<int>& v, string& ans) {
string cur(w.size(), '0');
dfs(0, 0, 0, W, w, v, cur, ans);
return maxV;
}
private:
void dfs(int s, int curW, int curV, int W, vector<int>& w, vector<int>& v, string& cur, string& ans) {
// 到达叶子结点,得到一个解,所以在这里更改最终结果
if (s >= w.size()) {
if (maxV < curV) {
ans.assign(cur);
maxV = curV;
}
return;
}
// as for goods s, two choices
for (int i = 0; i < 2; ++i) {
cur[s] = i + '0';
if (curW + i * w[s] <= W) {
curW += i * w[s];
curV += i * v[s];
dfs(s + 1, curW, curV, W, w, v, cur, ans);
curW -= i * w[s];
curV -= i * v[s];
}
}
}
int maxV = 0;
};
上面的程序可以通过剪枝进行优化,下来换一种思路:
令dp[i][j]表示前i件物品重量恰好为j时具有的最大价值,问题转化为求dp[N][0...W]的最大值,边界条件dp[0...N][0]=0:
假设3件物品,(w={1,1,2}),(v={1,2,4}),(W=2),先用递归形式分析,每件物品只有yes/no两种状态:
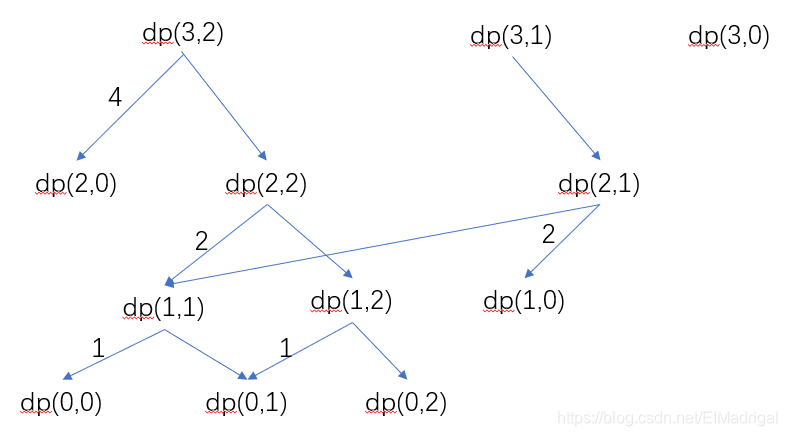
可以看到,求解过程中有很多重叠子问题,故可以采用记忆化递归求解,时间复杂度即为子问题数量(O(NW)),空间复杂度(O(NW))。
记忆化递归可以写成自底向上的动态规划,状态转移方程:
// dp->space complexity O(NW)
class knapsack01 {
public:
int knapsack(int W, vector<int>& w, vector<int>& v) {
const int N = w.size();
vector<vector<int>> dp(N + 1, vector<int>(W + 1, 0));
for(int i = 1;i <= N;++i)
for (int j = w[i - 1]; j <= W; ++j) {
dp[i][j] = max(dp[i - 1][j], v[i - 1] + dp[i - 1][j - w[i - 1]]);
}
return *max_element(dp[N].begin(), dp[N].end());
}
};
前i件物品只依赖于前i-1件物品,(dp)数组的更新方向为:
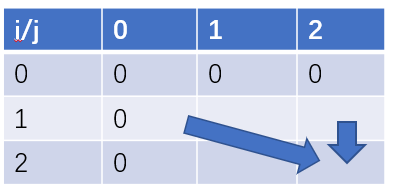
所以可以使用滚动数组降低空间复杂度为(O(W)):
// dp->space complexity O(W)
// method 1: use temp array
class knapsack01 {
public:
int knapsack(int W, vector<int>& w, vector<int>& v) {
const int N = w.size();
vector<int> dp(W + 1, 0);
for (int i = 1; i <= N; ++i) {
vector<int> temp(W + 1, 0);
for (int j = w[i - 1]; j <= W; ++j) {
temp[j] = max(temp[j], v[i - 1] + dp[j - w[i - 1]]);
}
dp.swap(temp);
}
return *max_element(dp.begin(), dp.end());
}
};
// method 2: use scrolling array
class knapsack01 {
public:
int knapsack(int W, vector<int>& w, vector<int>& v) {
const int N = w.size();
vector<int> dp(W + 1, 0);
for (int i = 1; i <= N; ++i) {
// iterate j reversely, avoid dp override
for (int j = W; j >= w[i - 1]; --j) {
dp[j] = max(dp[j], v[i - 1] + dp[j - w[i - 1]]);
}
}
return *max_element(dp.begin(), dp.end());
}
};
有一道比较类似的题目Target Sum,分析下此题顺便再练习下DP的套路。
题意是这样:给定一些非负数字,可以给每个数字添上+或-号,使得添加后的所有数字之和等于S。数组大小不超过20,S大小不超过1000。
我第一次做感觉这是个纯暴力DFS,枚举所有可能,复杂度(O(2^n))。
这道题和0/1背包不同之处在于:数组里的所有数字都必须用到。
接着我们试着做一些优化:
换种方式看问题:在这堆数字中选一些作为正数集合(P),剩下作为负数集合(N),那么有(sum(P)-sum(N)=S),(sum(P)+sum(N)+sum(P)-sum(N)=sum(nums)+S=2*sum(P)),故(sum(P)=(sum(nums)+S)/2),同时注意到(sum(nums)+S)是偶数。
所以问题转化为在数组中寻找一些数作为正数,使得这些数的和为((sum(nums)+S)/2),求这样的组合有多少种。这就转化为了0/1背包问题。
我们用(dp(i,j))表示从前i个数中选出和为j的方案数目,有状态转移方程(dp(i,j)=dp(i-1,j)+dp(i-1,j-nums[i])),如果纯粹暴力递归,有很多重叠子问题(类似背包问题的那个图)。Base Case就是,(dp(0,0)=1),即选出和为0的方案,就是每个都不选一种;否则当i = 0 || j < 0时,(dp(i,j)=0)。
所以先用记忆化搜索:
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int S) {
int sum = 0;
for (int num : nums)
sum += num;
vector<vector<int>> memo(21, vector<int>(1001, -1));
return sum < S || (sum + S) & 1 ? 0 : cnt(nums, memo, nums.size(), (sum + S) >> 1);
}
private:
int cnt(vector<int>& nums, vector<vector<int>>&memo, int idx, int sum) {
if (!idx && !sum)
return 1;
if (!idx || sum < 0)
return 0;
if (memo[idx][sum] > 0)
return memo[idx][sum];
memo[idx][sum] = cnt(nums, memo, idx - 1, sum) + cnt(nums, memo, idx - 1, sum - nums[idx - 1]);
return memo[idx][sum];
}
};
改一下Bottom-Up的形式,更新方向从左到右、从上到下,注意这里j不能从nums[i - 1]开始,否则j的前半部分无法更新到正确的值,后面如果用到就是错误的值。
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int S) {
int sum = 0;
for (int num : nums)
sum += num;
if (sum < S || (sum + S) & 1)
return 0;
vector<vector<int>> dp(21, vector<int>(1001, 0));
dp[0][0] = 1;
for (int i = 1; i <= nums.size(); ++i) {
// 不能for (int j = nums[i - 1]; j <= (sum + S) >> 1; ++j)
for (int j = 0; j <= (sum + S) >> 1; ++j) {
dp[i][j] = dp[i - 1][j];
if (j >= nums[i - 1]) {
dp[i][j] += dp[i - 1][j - nums[i - 1]];
}
}
}
return dp[nums.size()][(sum + S) >> 1];
}
};
最后来优化空间:(dp(i,j))取决于(dp(i-1,j))和(dp(i-1,j-num[i-1])),所以只要用一个一维数组(dp(j))记录上一行的所有值即可,这里必须反向更新,因为如果正向,上一行的j-num[i-1]位置已经被新值覆盖,计算结果出错。如果反向:上一行需要的2个位置都没有被覆盖:(dp(j)=dp(j)+dp(j-nums[i-1]))。
初始时候(0,0)位置为1,即(dp(0)=1),以后(dp(0))会不断更新。
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int S) {
int sum = 0;
for (int num : nums) {
sum += num;
}
return sum < S || (S + sum) & 1 ? 0 : numSubsetSum(nums, (S + sum) >> 1);
}
private:
int numSubsetSum(vector<int>& nums, int target) {
vector<int> dp(target + 1, 0);
dp[0] = 1;
for (int i = 0; i < nums.size(); ++i) {
/* 等价写法
for (int j = target; j >= 0; --j){
if (j - nums[i] >= 0)
dp[j] += dp[j - nums[i]];
} */
// 只有j>=nums[i]才更新,否则沿用上一行的值
for (int j = target; j >= nums[i]; --j) {
dp[j] += dp[j - nums[i]];
}
}
return dp[target];
}
};
完全背包
- 每件物品可以使用任意多次。
- 一个Naive的思路: 虽然题目描述每件物品可以使用任意多次,但实际上由于W的限制,每件物品最多使用(lfloor W/w[i] floor)次。这样我们可以将每件物品拆为(lfloor W/w[i] floor)件,问题就转化为了0-1背包。子问题仍然有NW个,但是求解每个子问题需要(O(W/w[i])),总的时间复杂度(O(Sigma (W/w[i])*W)),也即(O(W*拆后物品件数))。
- 更tricky的做法:W无法改变,只能改变拆后物品件数。这里可以使用二进制的思想:假设我们某件物品可以使用(10=8+2)次,原本需要复制出10件,现在只要复制出2件,价值和重量是原来的8倍和2倍,这样就降低了复杂度。
- 完全背包有(O(NW))的算法。
多重背包
- 每件物品最多可以使用(num[i])次。
- 同样,Naive的思路就是将每件物品都复制(num[i])次,问题转化为0-1背包,复杂度(O(Sigma nums[i]*W))。
- 将(num[i])用二进制表示,价值和重量变为原来的相应倍,降低复杂度。
Future
后续还有混合背包、二维费用的背包等,详情可以学习背包九讲。