UVa 10382 - Watering Grass
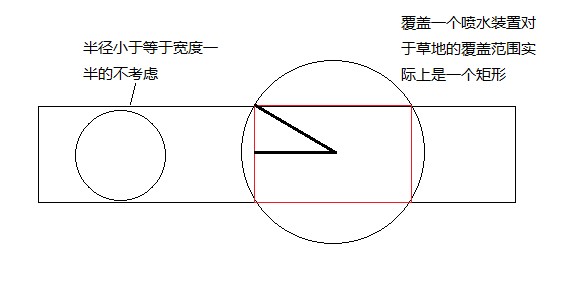
n sprinklers are installed in a horizontal strip of grass l meters long and w meters wide. Each sprinkler is installed at the horizontal center line of the strip. For each sprinkler we are given its position as the distance from the left end of the center line and its radius of operation.
What is the minimum number of sprinklers to turn on in order to water the entire strip of grass?
Input
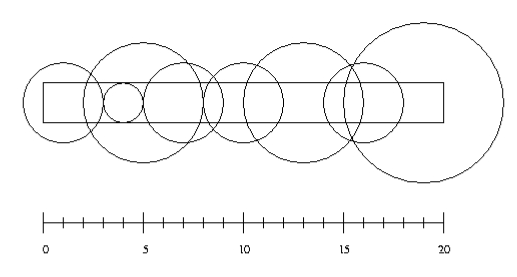
Input consists of a number of cases. The first line for each case contains integer numbers n, l and w with n <= 10000. The next n lines contain two integers giving the position of a sprinkler and its radius of operation. (The picture above illustrates the first case from the sample input.)
Output
For each test case output the minimum number of sprinklers needed to water the entire strip of grass. If it is impossible to water the entire strip output -1.
Sample input
8 20 2
5 3
4 1
1 2
7 2
10 2
13 3
16 2
19 4
3 10 1
3 5
9 3
6 1
3 10 1
5 3
1 1
9 1
Sample output
2
-1
1 #include <bits/stdc++.h> 2 using namespace std; 3 inline int read() 4 { 5 int x=0,f=1; 6 char ch=getchar(); 7 while(ch<'0'||ch>'9') 8 { 9 if(ch=='-') 10 f=-1; 11 ch=getchar(); 12 } 13 while(ch>='0'&&ch<='9') 14 { 15 x=x*10+ch-'0'; 16 ch=getchar(); 17 } 18 return x*f; 19 } 20 inline void write(int x) 21 { 22 if(x<0) 23 { 24 putchar('-'); 25 x=-x; 26 } 27 if(x>9) 28 { 29 write(x/10); 30 } 31 putchar(x%10+'0'); 32 } 33 struct Node 34 { 35 double x,y; 36 }p[10005]; 37 int cmp(const Node &a,const Node &b) 38 { 39 if(a.x<b.x) 40 return 1; 41 else 42 return 0; 43 } 44 int main() 45 { 46 int n; 47 double l,w; 48 while(scanf("%d%lf%lf",&n,&l,&w)!=EOF) 49 { 50 for(int i=0;i<n;i++) 51 { 52 double s,r; 53 scanf("%lf%lf",&s,&r); 54 if(r<w/2.0-1e-6||fabs(r-w/2.0)<1e-6) 55 { 56 i--; 57 n--; 58 continue; 59 } 60 double x=sqrt(r*r-w*w/4.0); 61 p[i].x=s-x; 62 p[i].y=s+x; 63 if(p[i].x<1e-6) 64 p[i].x=0; 65 if(p[i].y>l+1e-6) 66 p[i].y=l; 67 } 68 sort(p,p+n,cmp); 69 if(fabs(p[0].x)>1e-6) 70 { 71 printf("-1 "); 72 continue; 73 } 74 double pos=0,maxx=0; 75 int sum=0; 76 while(1) 77 { 78 if(pos>=l) 79 break; 80 maxx=0; 81 for(int i=0;i<n;i++) 82 if((p[i].x<pos-1e-6||fabs(p[i].x-pos)<1e-6)&&p[i].y>pos+1e-6) 83 { 84 if(p[i].y>maxx+1e-6) 85 { 86 maxx=p[i].y; 87 } 88 } 89 if(fabs(maxx)<1e-6) 90 { 91 sum=0; 92 break; 93 } 94 sum++; 95 pos=maxx; 96 } 97 if(sum==0) 98 printf("-1 "); 99 else 100 printf("%d ",sum); 101 } 102 return 0; 103 }