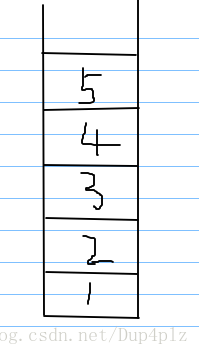7-3 堆栈模拟队列（25 point(s)） 【数据结构】

7-3 堆栈模拟队列（25 point(s)）

设已知有两个堆栈S1和S2，请用这两个堆栈模拟出一个队列Q。

所谓用堆栈模拟队列，实际上就是通过调用堆栈的下列操作函数:

int IsFull(Stack S)：判断堆栈S是否已满，返回1或0；
int IsEmpty (Stack S )：判断堆栈S是否为空，返回1或0；
void Push(Stack S, ElementType item )：将元素item压入堆栈S；
ElementType Pop(Stack S )：删除并返回S的栈顶元素。

实现队列的操作，即入队void AddQ(ElementType item)和出队ElementType DeleteQ()。
输入格式:

输入首先给出两个正整数N1和N2，表示堆栈S1和S2的最大容量。随后给出一系列的队列操作：A item表示将item入列（这里假设item为整型数字）；D表示出队操作；T表示输入结束。
输出格式:

对输入中的每个D操作，输出相应出队的数字，或者错误信息ERROR:Empty。如果入队操作无法执行，也需要输出ERROR:Full。每个输出占1行。
输入样例:

3 2
A 1 A 2 A 3 A 4 A 5 D A 6 D A 7 D A 8 D D D D T

输出样例:

ERROR:Full
1
ERROR:Full
2
3
4
7
8
ERROR:Empty

思路
用小容量栈 来作为 入队栈 大容量栈 来作为出队栈
当小容量栈 满 并且 大容量栈不为空的时候 这时候就是队满
因为 出队栈还没出完 也就是 入队栈的元素还不能够转移到出队栈 而入队栈 又满了 这时候 就没法入队了

然后 出队的时候 两栈均为空的时候 就是 栈空

如果出队栈为空 那么先要把 入队栈的所有元素都转移到 出队栈 然后再从 出队栈 出队 这就是为什么要用 小容量栈 来作为 入队栈

然后 为什么要这样做呢

因为 栈的特点是 先入后出

那么 入队栈 的所有元素 压入 出队栈后 出队栈的栈顶元素 就是先入的
就满足队列的性质

比如 1 2 3 4 5

然后 进入 入队栈

就是

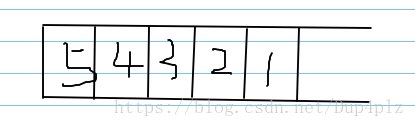
但是 出队的顺序 应该是

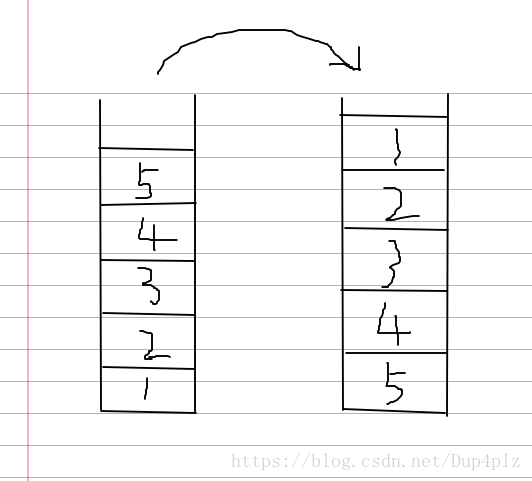
所以 我们借用另一个 出队栈

通过从 入队栈 一个一个 pop 然后 一个一个 push 进 出队栈

然后要出队 就可以实现了

所以 要满足 出队栈的容量 大于等于 入队栈的容量

AC代码

#include <cstdio>
#include <cstring>
#include <ctype.h>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <map>
#include <stack>
#include <set>
#include <numeric>
#include <sstream>
#include <iomanip>
#include <limits>

#define CLR(a) memset(a, 0, sizeof(a))
#define pb push_back

using namespace std;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair <int, int> pii;
typedef pair <ll, ll> pll;
typedef pair<string, int> psi;
typedef pair<string, string> pss;

const double PI = 3.14159265358979323846264338327;
const double E = exp(1);
const double eps = 1e-30;

const int INF = 0x3f3f3f3f;
const int maxn = 1e4 + 5;
const int MOD = 1e9 + 7;

stack <int> s1, s2;

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    if (n > m)
        swap(n, m);
    char c;
    int len, num;
    while (scanf(" %c", &c) && c != 'T')
    {
        if (c == 'A')
        {
            scanf("%d", &num);
            if (s1.size() == n && s2.size() != 0)
                printf("ERROR:Full
");
            else if (s1.size() == n)
            {
                len = s1.size();
                while (len--)
                {
                    int temp = s1.top();
                    s1.pop();
                    s2.push(temp);
                }
                s1.push(num);
            }
            else
                s1.push(num);
        }
        else
        {
            if (s1.size() == 0 && s2.size() == 0)
                printf("ERROR:Empty
");
            else 
            {
                if (s2.size() == 0)
                {
                    int len = s1.size();
                    while (len--)
                    {
                        int temp = s1.top();
                        s1.pop();
                        s2.push(temp);
                    }
                }
                printf("%d
", s2.top());
                s2.pop();
            }
        }
    }
}