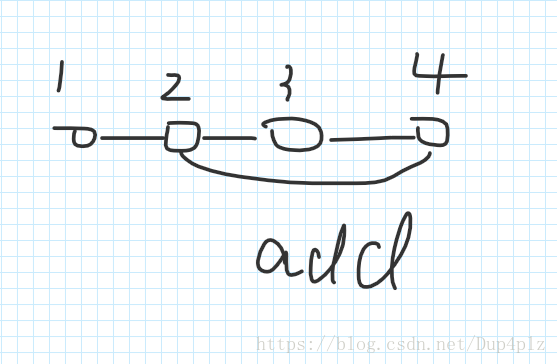题目链接
http://acm.hdu.edu.cn/showproblem.php?pid=4081
题意
给出n个城市的坐标 以及 每个城市里面有多少人
秦始皇想造路 让每个城市都连通 (直接或者间接都可以)
然后 有一个特别厉害的大臣 可以造一条魔法路 不用耗费资金 但是要求 这条路链接的两座城市的人要尽量多
定义了一个 value = A/B
A = 魔法路链接的两座城市的总人数
B = 除了魔法路,其他路的总权值
求出最大的value
思路
首先我会想到最小生成树
然后我想让value 最大 我就想 能不能 去枚举每一条边 当做 魔法路
因为 求最小生成树 要保证 value 尽量小
然后枚举每一条边的时候
如果这条边已经在最小生成树里面了 那么此时的ans = (A[i] + A[j] / ans - G[i][j])
B = 答案 - 这条边
这个应该比较好理解
如果没有在最小生成树里面 ,那么此时的B = ans - Max[i][j]
为什么是这样呢。。
Max[i][j] 表示 从i - j 的最大边
因为 我们枚举的这条边 没有在 这条边 所以加入这条边之后 i - j 之间 就会形成一个环路
比如说 是这样的
自然就可以发现 我们在 2 - 4 之间已经在最小生成树里面的边 可以拆掉一条
那么拆哪一条呢,, 为了对答案有更大贡献,自然是边权最大的那条
AC代码
#include <cstdio>
#include <cstring>
#include <ctype.h>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <map>
#include <stack>
#include <set>
#include <list>
#include <numeric>
#include <sstream>
#include <iomanip>
#include <limits>
#define CLR(a, b) memset(a, (b), sizeof(a))
#define pb push_back
#define bug puts("***bug***");
#define fi first
#define se second
#define stack_expand #pragma comment(linker, "/STACK:102400000,102400000")
#define syn_close ios::sync_with_stdio(false);cin.tie(0);
//#define bug
//#define gets gets_s
using namespace std;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair <int, int> pii;
typedef pair <ll, ll> pll;
typedef pair <string, int> psi;
typedef pair <string, string> pss;
typedef pair <double, int> pdi;
const double PI = acos(-1.0);
const double E = exp(1.0);
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;
const int maxn = 1e3 + 10;
const int MOD = 142857;
int n;
double G[maxn][maxn];
struct node
{
int x, y, p;
node() {}
node(int x, int y, int p) : x(x), y(y), p(p) {}
void read()
{
scanf("%d%d%d", &x, &y, &p);
}
}point[maxn];
double dis(int a, int b)
{
double d1 = (point[a].x - point[b].x) * (point[a].x - point[b].x) * 1.0;
double d2 = (point[a].y - point[b].y) * (point[a].y - point[b].y) * 1.0;
return sqrt(d1 + d2);
}
int used[maxn][maxn];
double Max[maxn][maxn];
double lowcost[maxn];
int pre[maxn];
int visit[maxn];
double ans;
int findMin()
{
double Maxc = INF * 1.0;
int flag = 0;
for (int i = 1; i <= n; i++)
{
if (visit[i] == 0 && lowcost[i] < Maxc)
{
Maxc = lowcost[i];
flag = i;
}
}
return flag;
}
void prime()
{
for (int i = 1; i <= n; i++)
{
visit[i] = 0;
lowcost[i] = INF * 1.0;
used[i][i] = 0;
Max[i][i] = -INF * 1.0;
for (int j = i + 1; j <= n; j++)
{
Max[i][j] = Max[j][i] = -INF * 1.0;
used[i][j] = used[j][i] = 0;
}
}
for (int i = 1; i <= n; i++)
{
lowcost[i] = Max[1][i] = G[1][i];
pre[i] = 1;
}
pre[1] = -1;
visit[1] = 1;
ans = 0.0;
for (int i = 2; i <= n; i++)
{
int k = findMin();
visit[k] = 1;
ans += lowcost[k];
used[pre[k]][k] = used[k][pre[k]] = 1;
for (int j = 1; j <= n; j++)
{
if (visit[j] == 1 && j != k)
Max[j][k] = Max[k][j] = max(Max[j][pre[k]], lowcost[k]);
if (visit[j] == 0 && lowcost[j] > G[k][j])
{
lowcost[j] = G[k][j];
pre[j] = k;
}
}
}
}
double smst()
{
double Maxc = 0.0;
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++)
if (used[i][j] == 0)
Maxc = max(Maxc, (point[i].p + point[j].p) * 1.0 / (ans - Max[i][j]));
else
Maxc = max(Maxc, (point[i].p + point[j].p) * 1.0 / (ans - G[i][j]));
return Maxc;
}
void clear()
{
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
G[i][j] = 0.0;
}
int main()
{
int t;
cin >> t;
while (t--)
{
scanf("%d", &n);
clear();
for (int i = 1; i <= n; i++)
point[i].read();
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++)
G[i][j] = G[j][i] = dis(i, j);
prime();
printf("%.2lf
", smst());
}
}
/*
先跑最小生成树
然后去枚举每一条边 当做 magic road
如果该边本来就在最小生成树当中 那么我就删去这条边 维护答案
如果该边本来没有在最小生成树当中,那么我就删去i - j 中的最大边 维护答案
*/