放大器应用

反相放大器

　　

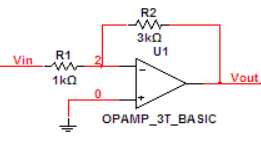
　　分析：设放大器为理想放大器。图中点2处电压为V-，点0处电压为V+ 。由于是负反馈，V+=V- ,因为正向输入端接地，所以 V+=V-=0又由于输入阻抗高，以至于（几乎）无电流流入放大器，所以流过R2的电流和流过R1的电流大小相等（为 Vin/R1），而V_- = V_out + R2 * iR2 =  Vout + R2 * (Vin/R1)。所以得到 Vout = -Vin * (R2/R1) 。增益为 -R2/R1 ，该值与放大器开环增益A无关，输入与输出反相。

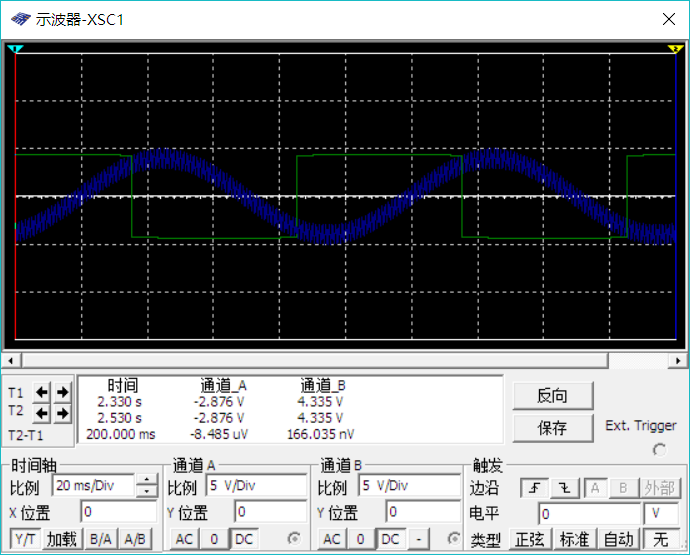
　　输入输出波形如下（模拟环境，蓝色输入，绿色输出）

　　

 

正相放大器

　　

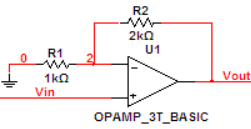
　　分析：分析方法与反相放大器相似。V₊ = V_- =V_in ， i_R2=i_R1=V_in/R1 ,  V_out = V_- + R2 * i_R2 =V_in + V_in * (R2/R1) 。整理一下，V_out = V_in * (1 + R2/R1) ,增益为 (1 + R2/R1)。

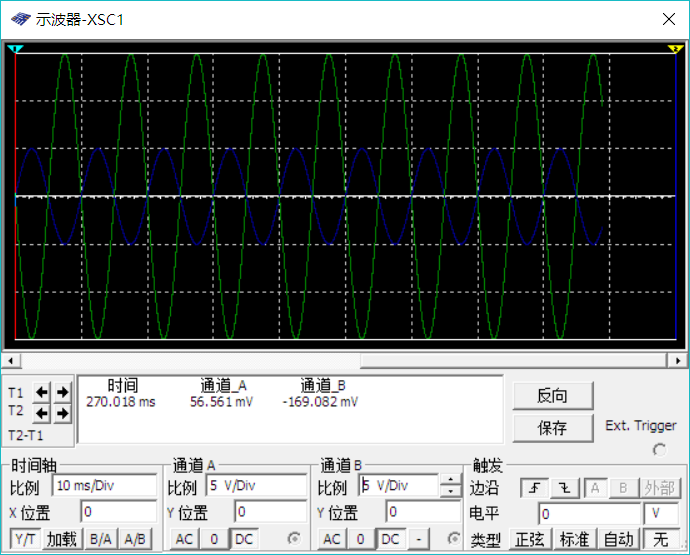
　　输入输出波形如下（模拟环境，蓝色输入，绿色输出）

　　

微分电路

　　

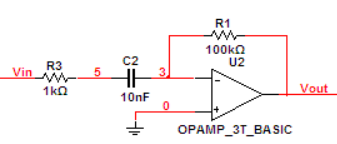
　　原理：利用了流过电容的电流是其两端电压对时间的微分的特性。

　　　　

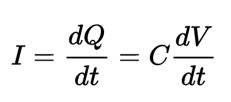
　　电路表现：V_out 正比于V_in 对时间的微分。

　　分析：电路中R3作用是提高电路稳定性，在研究电路性质时可暂时忽略（可在R1处并联一个小电容进一步提高稳定性）。思路在于将输入电压加到电容上，得到的电流便是电压对时间的微分，然后利用放大器输入阻抗高的特点，使电容电流完全流入电阻R1，获得电压，则此电压与输入电压对时间的微分成正比。图中流经C2的电流大小等于流经R1的电流大小，C2两端电压为V_in, 故i_R1 =i_C2=C * (dVin/dt) 。又有V_out = -R1 * i_{R1 。}

　　所以V_out = -R1*C* (dV_in/dt) 。可知V_out 与V_in对时间的微分成正比。

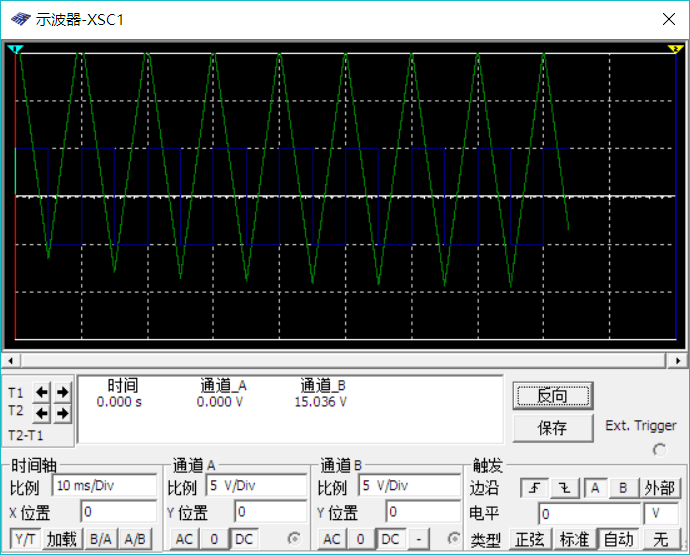
　　输入输出波形如下（模拟环境，蓝色输入，绿色输出）

　　

积分电路

　　

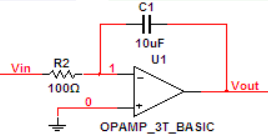
　　利用了电容两端电压是通过它的电流的积分的性质。

　　电路表现：V_out 正比于V_in 对时间的积分。

　　分析：类似于微分电路，此处将输入电压加在电阻上得到电流，再使此电流流经电容，从而获得与输入的积分成正比的输出。

　　输入输出波形如下（模拟环境，蓝色输入，绿色输出）

　　

 比较器

　　

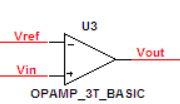
　　由于放大器开环增益大，所以V_out始终饱和，V_in > V_ref 时输出为正向最大，V_in < V_ref时输出为负向最大。如果输入有噪声，在输入接近零点处可能会造成输出不稳定。

　　无噪声输入输出波形如下（模拟环境，蓝色输入，绿色输出，V_res=0V）

　　

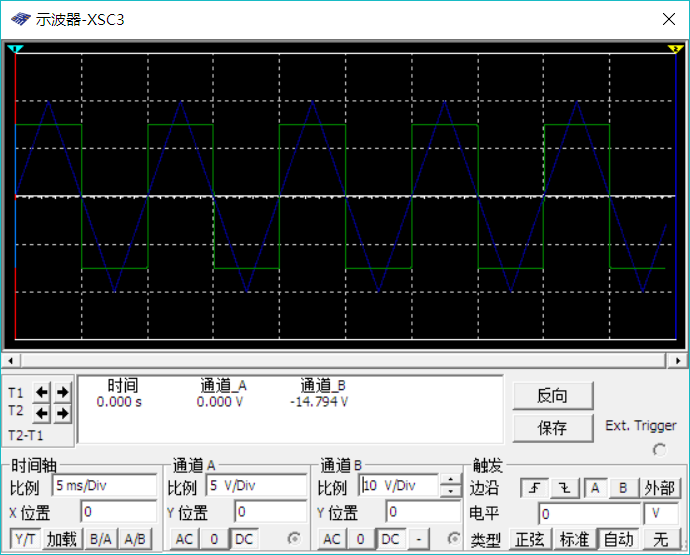
滞回比较器

　　

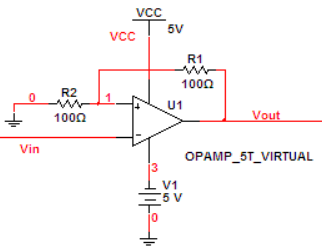
　　以上图为例，V_out 可能是+5V或-5V，当V_out为+5V时，V₊为V_out * R2/(R1+R2)，在上图情况即为2.5V，则当V_in > 2.5V 时，输出翻转，此时V₊为-2.5V，只有当V_in < -2.5V时输出才能再次翻转。 

　　滞回曲线如图

　　

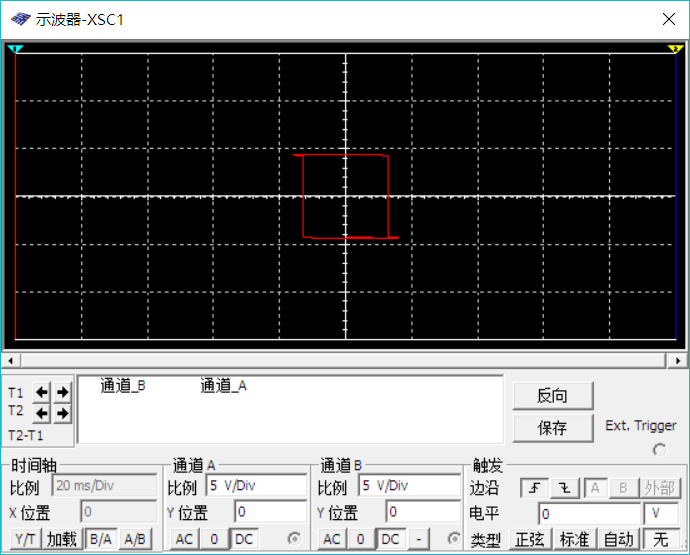
　　输入输出波形如下（模拟环境，蓝色输入，绿色输出）