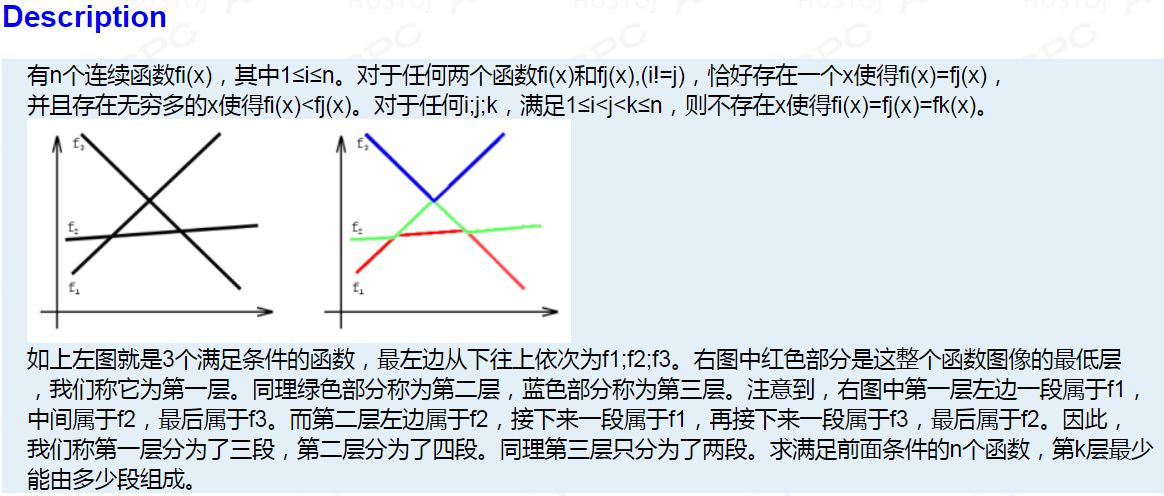
【题解】
明显是道数学题。
需要在草稿纸上写写画画,在这里我只写一些结论。
首先我们可以发现,当k恒定时,不管n增加到多大,第k层的最少段数都是不变的。因为我们必定可以找到一种加入一条新的直线的方式,使得这条直线与之前的n条直线的n个交点中,n-1个在第k层的上方,1个在第k层上,且使得原来第k层最左边或者最右边的一个交点不再属于第k层。这样的话,第k层上面的交点数量不变,段数也就不变。
接着我们可以发现,当直线数是偶数的时候,第k层的最左边与最右边的两条线段的斜率一定不同,所以我们可以通过加入一条直线,使这条直线与第k层只有两个交点,且这两个交点处于最左边与最右边。这样第k层将变为第k+1层,同时段数增加2.
那么考虑我们逐步添加直线构造符合的图形,我们在奇数条直线的时候通过结论1增加一条直线,使得线段条数变为偶数且某一层的段数不变。在偶数条线段的时候我们可以根据结论2把这一层上推一层或者仅仅是根据结论2增加一条直线。这取决于k的大小。
#include<cstdio>
#include<algorithm>
using namespace std;
int n,k;
inline int read(){
int k=0,f=1; char c=getchar();
while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar();
while('0'<=c&&c<='9')k=k*10+c-'0',c=getchar();
return k*f;
}
int main(){
n=read(); k=read();
if(n==1) puts("1");
else printf("%d
",2*min(k,n-k+1));
return 0;
}