Bit Magic
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1383 Accepted Submission(s): 398
Problem Description
Yesterday, my teacher taught me about bit operators: and (&), or (|), xor (^). I generated a number table a[N], and wrote a program to calculate the matrix table b[N][N] using three kinds of bit operator. I thought my achievement would get teacher's attention.
The key function is the code showed below.
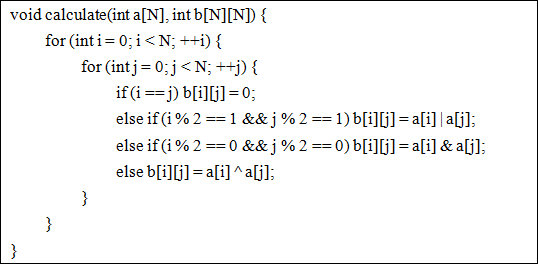
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
The key function is the code showed below.
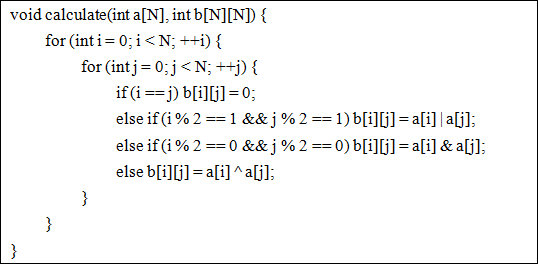
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
Input
There are multiple test cases.
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
Output
For each test case, output "YES" if corresponding number table a[N] exists; otherwise output "NO".
Sample Input
2
0 4
4 0
3
0 1 24
1 0 86
24 86 0
Sample Output
YES
NO
Source
Recommend
zhuyuanchen520
/* * Author: * Created Time: 2013/10/25 20:53:54 * File Name: A.cpp * solve: A.cpp */ #include<cstdio> #include<cstring> #include<cstdlib> #include<cmath> #include<algorithm> #include<string> #include<map> #include<stack> #include<set> #include<iostream> #include<vector> #include<queue> //ios_base::sync_with_stdio(false); //#pragma comment(linker, "/STACK:1024000000,1024000000") using namespace std; #define sz(v) ((int)(v).size()) #define rep(i, a, b) for (int i = (a); i < (b); ++i) #define repf(i, a, b) for (int i = (a); i <= (b); ++i) #define repd(i, a, b) for (int i = (a); i >= (b); --i) #define clr(x) memset(x,0,sizeof(x)) #define clrs( x , y ) memset(x,y,sizeof(x)) #define out(x) printf(#x" %d ", x) #define sqr(x) ((x) * (x)) typedef long long LL; const int INF = 1000000000; const double eps = 1e-8; const int maxn = 510; int sgn(const double &x) { return (x > eps) - (x < -eps); } int b[maxn][maxn]; int c[maxn][maxn]; int a[maxn]; int n; bool cal(int x,int y) { a[0] = x; rep(i,0,n) rep(j,0,n) c[i][j] = (b[i][j] >> y) & 1;//枚举每一位 rep(i,1,n) a[i] = (c[i][i-1] == 0 ? a[i-1] : 1 - a[i-1]); rep(i,0,n) rep(j,0,n) { if(i == j) { if(c[i][j]) return 0; }else if(i%2 == 1 && j%2 == 1) { if(c[i][j] != (a[i]|a[j])) return 0; }else if(i%2 == 0 && j%2 == 0) { if(c[i][j] != (a[i]&a[j])) return 0; }else { if(c[i][j] != (a[i] ^ a[j])) return 0; } } return 1; } bool solve() { repf(i,0,31) if(!cal(0,i) && !cal(1,i)) return 0; return 1; } int main() { //freopen("in.txt","r",stdin); while(scanf("%d",&n) == 1) { rep(i,0,n) rep(j,0,n) scanf("%d",&b[i][j]); if(solve()) cout<<"YES"<<endl; else cout<<"NO"<<endl; } return 0; }
后续附上2-Sat的解法