1963. Kite
Time limit: 1.0 second
Memory limit: 64 MB
Memory limit: 64 MB
Vova bought a kite construction kit in a market in Guangzhou. The next day the weather was good and he decided to make the kite and fly it. Manufacturing instructions, of course, were only in Chinese, so Vova decided that he can do without it. After a little tinkering, he constructed a kite in the form of a flat quadrangle and only needed to stick a tail to it.
And then Vova had to think about that: to what point of the quadrangle's border should he stick the kite tail? Intuition told him that in order to make the kite fly steadily, its tail should lie on some axis of symmetry of the quadrangle. On the left you can see two figures of stable kites, and on the right you can see two figures of unstable kites.
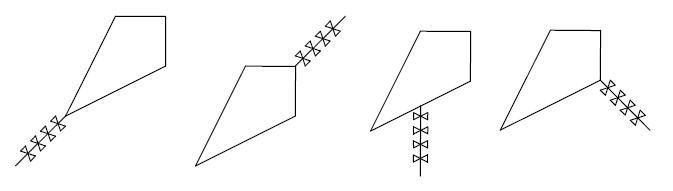
How many points on the quadrangle border are there such that if we stick a tail to them, we get a stable kite?
Input
The four lines contain the coordinates of the quadrangle's vertices in a circular order. All coordinates are integers, their absolute values don't exceed 1 000. No three consecutive quadrangle vertices lie on the same line. The opposite sides of the quadrangle do not intersect.
Output
Print the number of points on the quadrangle border where you can attach the kite.
Samples
| input | output |
|---|---|
0 0 1 2 2 2 2 1 |
2 |
0 0 2 1 2 2 0 2 |
0 |
Hint
The axis of symmetry of a flat figure is a straight line lying in the figure plane and dividing the figure to the two halves that are each other's mirror image.
Problem Author: Alexander Ipatov
Problem Source: Open Ural FU Personal Contest 2013
Problem Source: Open Ural FU Personal Contest 2013
Tags: none
Difficulty: 373 Printable version Submit solution Discussion (1)
All submissions (897) All accepted submissions (265) Solutions rating (176)
All submissions (897) All accepted submissions (265) Solutions rating (176)
暴力判断对角线以及对边的情况
有一个对称轴ans+=2!
int main() { //freopen("in.txt","r",stdin); rep(i,0,4) p[i] = read_point(); int ans = 0; Vector ac = p[0] - p[2]; Vector bd = p[1] - p[3]; Vector ab = p[0] - p[1]; Vector ad = p[0] - p[3]; Vector bc = p[1] - p[2]; Vector cd = p[2] - p[3]; if(Dot(ac,bd) == 0) { if(dcmp(Angle(ad,ac) - Angle(ab,ac)) == 0) { ans ++; } if(dcmp(Angle(bd,bc) - Angle(bd,Point(0,0)-ab)) == 0) { ans ++; } } Point hab = half(p[0],p[1]); Point had = half(p[0],p[3]); Point hcd = half(p[2],p[3]); Point hcb = half(p[2],p[1]); Vector h12 = hab - hcd; Vector h34 = had - hcb; if(Dot(h12,ab) == 0 && Dot(h12,cd) == 0) ans ++; if(Dot(h34,ad) ==0 && Dot(h34,bc) == 0) ans++; cout<<ans*2<<endl; return 0; }