引言:
在求解机器学习算法模型参数即无约束优化问题时,最常用到的就是梯度下降算法和最小二乘法。
给定一个与参数 θ 有关的目标函数 J(θ), 求使得 J 最小的参数 θ.
针对此类问题, 梯度下降通过不断往梯度的负方向移动参数来求解。
首先需要搞明白的小概念:
1.梯度和导数的区别是:函数的梯度形成了一个向量场。
2.梯度的定义:
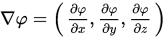
分类:
主要包括BGD,SGD,MBGD三种算法。区别主要在于用多少样本数据来计算目标函数的梯度,从而在准确性和优化速度之间做权衡。
1 Batch gradient descent (BGD)
Vanilla gradient descent 又称为 Batch gradient descent (BGD),其需要计算整个训练集的梯度,即:
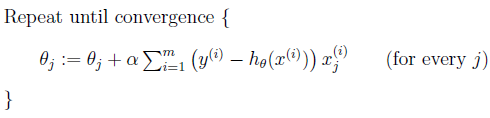 其中 a 为学习率,用来控制更新的“力度”。
其中 a 为学习率,用来控制更新的“力度”。
优点:
对于凸目标函数,可以保证全局最优; 对于非凸目标函数,可以保证一个局部最优。
缺点:
速度慢; 数据量大时不可行; 无法在线优化(即无法处理动态产生的新样本)。
2 Stochastic gradient descent (SGD)
Stochastic gradient descent (SGD),仅计算某个样本的梯度,即针对某一个训练样本 xixi 及其label yiyi更新参数:

逐步减小学习率,SGD表现得同BGD很相似,最后都可以有不错的收敛。
优点:
更新频次快,优化速度更快; 可以在线优化(可以无法处理动态产生的新样本);一定的随机性导致有几率跳出局部最优(随机性来自于用一个样本的梯度去代替整体样本的梯度)
缺点:
随机性可能导致收敛复杂化,即使到达最优点仍然会进行过度优化,因此SGD得优化过程相比BGD充满动荡;
用处:
随机梯度下降也适用于样本数量不多,特征也不多的情况。
3 Mini-batch gradient descent (MBGD)
Mini-batch gradient descent (MBGD) 计算包含m个样本的mini-batch的梯度:
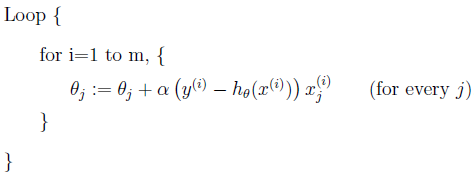
MBGD是训练神经网络最常用的优化方法。
优点:
参数更新时的动荡变小,收敛过程更稳定,降低收敛难度;可以利用现有的线性代数库高效的计算多个样本的梯度
4.带动量的SGD:
动量的引入是为了加速SGD的优化过程。
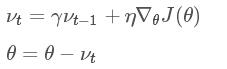
分析上式就会明白动量的作用原理:利用惯性,即当前梯度与上次梯度进行加权,如果方向一致,则累加导致更新步长变大;如果方向不同,则相互抵消中和导致更新趋向平衡。
动量 y常被设定为0.9或者一个相近的值。
5 Nesterov accelerated gradient(NAG)
带动量的SGD可以加速超车,但是却不知道快到达终点时减速。 Nesterov accelerated gradient (NAG)就是用来解决这个问题的。改进的目的就是为了提前看到前方的梯度。如果前方的梯度和当前梯度目标一致,那我直接大步迈过去; 如果前方梯度同当前梯度不一致,那我就小心点更新。

很明显,同带动量的SGD相比,梯度不是根据当前位置 θ计算出来的,而是在移动之后的位置(θ−γνt−1)计算梯度。 (已经确定会移动 γνt−1,那不如之前去看移动后的梯度)

蓝色线指的是带动量SGD的两次的移动方向;棕色线是计划移动的量( γνt−1 ); 红色线是在移动后位置计算的移动量; 棕色线和红色线的合并效果就是绿色线NAG。
梯度下降的矩阵实现的具体过程:https://www.cnblogs.com/pinard/p/5970503.html
挑战:
需要考虑的问题有:
1、如何选择合适的学习率
2、如何确定调整学习率的策略
3、如何跳出局部最优
4、对于参数更新选择相同的学习率是否妥当
算法优化可选的方向:
1.算法步长的选择:见下面的介绍
2.算法的初始参数的选择,需要多次选择不同的初始化值运算,然后在所有计算结果中选择最小化的值。
3对数据进行归一化。由于样本不同特征的取值范围不一样,可能导致迭代很慢,为了减少特征取值的影响,可以对特征数据归一化,也就是对于每个特征x,求出它的期望x¯和标准差std(x),然后转化为:
(x−x¯)/std(x)
这样特征的新期望为0,新方差为1,迭代次数可以大大加快。
关于步长选择:
步长选择对下降速度影响较大,选择合适的步长才能得到较好的结果,步长过大会使得结果发散,步长过小会使得结果收敛较慢,对于步长选择主要由以下几种方法:
1固定常数
2.线性变化:随着迭代次数的增加,步长不断减小
3.线性搜索方法:http://blog.csdn.net/wangjian1204/article/details/50284455