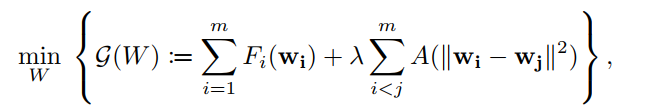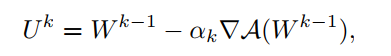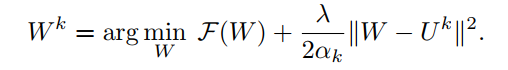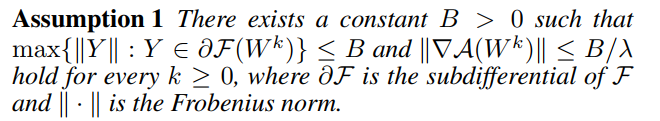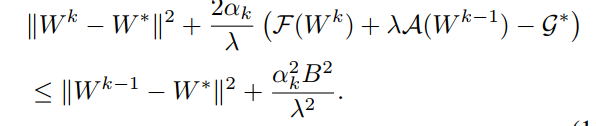Methods
In their dissertation, in order to specialize clients' models, an intermediate result (U^k) was computed as an aggregated model and forced clients' model ({mathbf W}) to be closed to (U^k).
Concretely, they solve the following problem:
where (A) is a kind of similarity measure. The objective function is alternatively optimized by optimizing (U^k) and ({mathbf W}^k). First, (U^k) only depends on the second term (sum A(Vert{mathbf w}_i -{mathbf w}_j Vert^2)),where ({mathbf w}_i) denotes (i)-th column of ({mathbf W}) and the total number of clients is (m). (U^k) is computed by
Then, ({mathbf W}^k) is the solution of
The complete algorithm procedure is following
Note: (W^{k}) is the optimal solution of the above problem in k-th step. In my opinion, it's unlikely to find a closed solution and needs multi-local steps to find ({mathbf W}^k). Because authors didn't publish their code, I can't check the optimal condition of ({mathbf W}^{k}).
Convergence
For simplicity, there is only a convergence analysis in convex setting in this blog. Before elaborating the process, let take a look at their assumption:
(L-) smooth is the only required condition and their analysis is based on that solving ({mathbf W}^k) is feasible.
As discussed in my previous bolg, we should prove ({mathbf W}^k) is convergent to ({mathbf W}^*) along with (k o infty). According to the definition of strongly convex, we have
plugging in (U^k = {mathbf W}^{k-1}-alpha_k abla{mathcal A}({mathbf W}^{k-1})),
we can have
we still should find the relationship between ({mathcal F}({mathbf W}^{k})) and ({mathcal F}({mathbf W}^{k-1})).
Summary
- In their work, authors recognized that the similarity measure (Vert {mathbf w}_i-{mathbf w}_jVert) is improper in deep network.
- As above said, find ({mathbf W}^k) in a closed form is difficult in most scenario
- The message passing mechanism is ambiguous for me