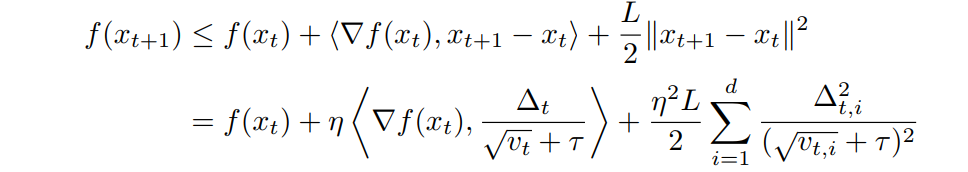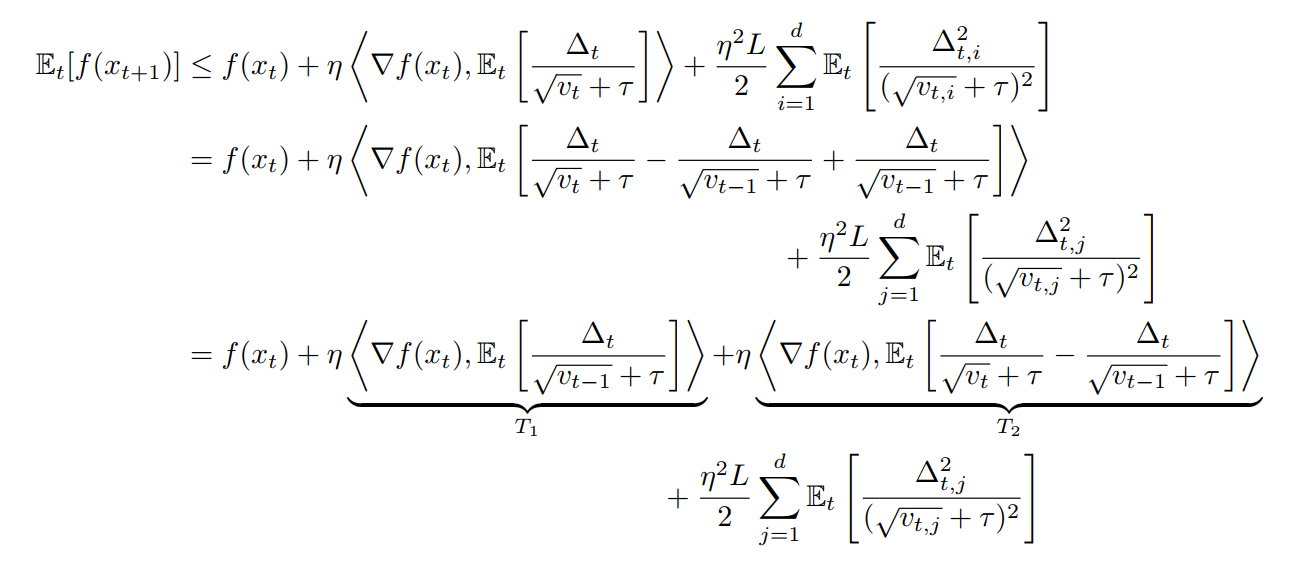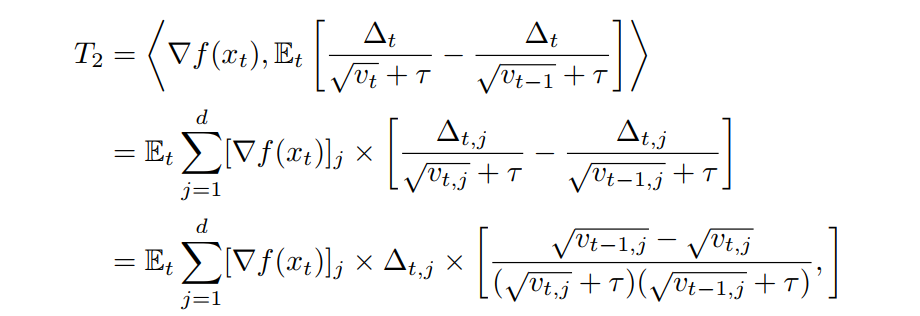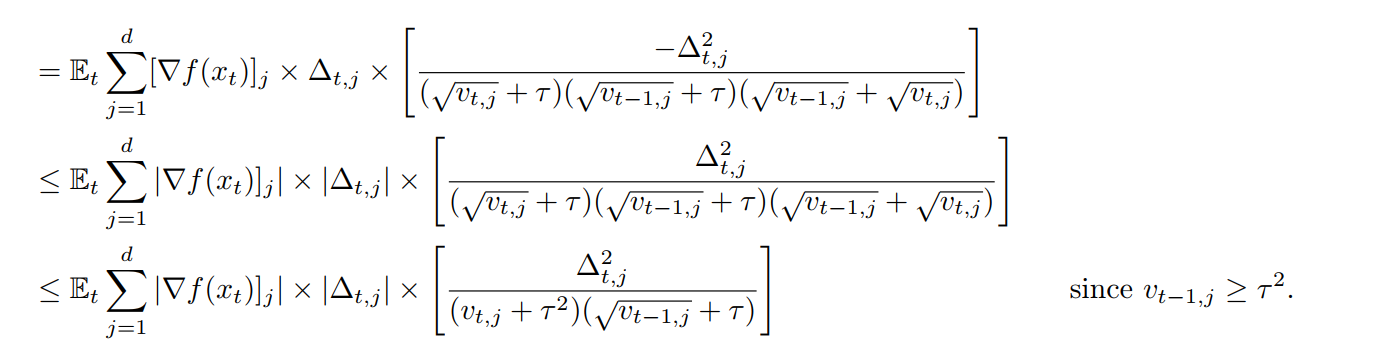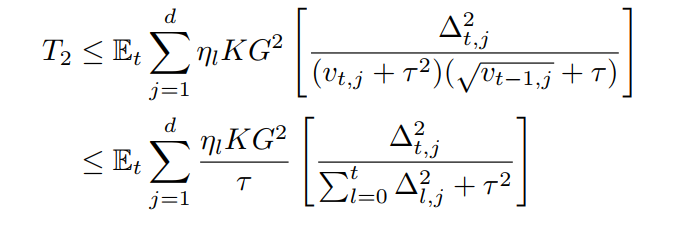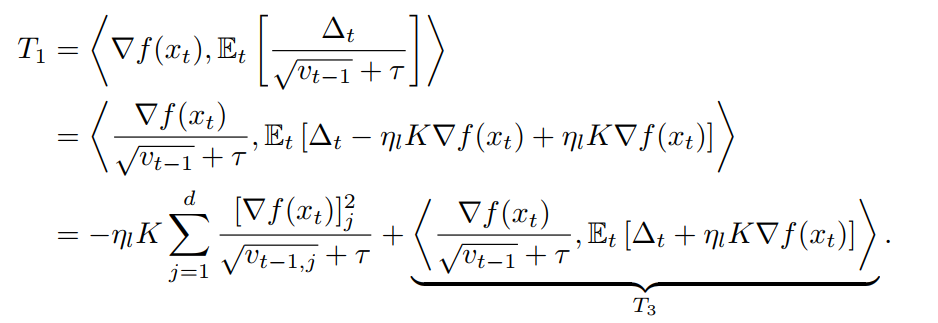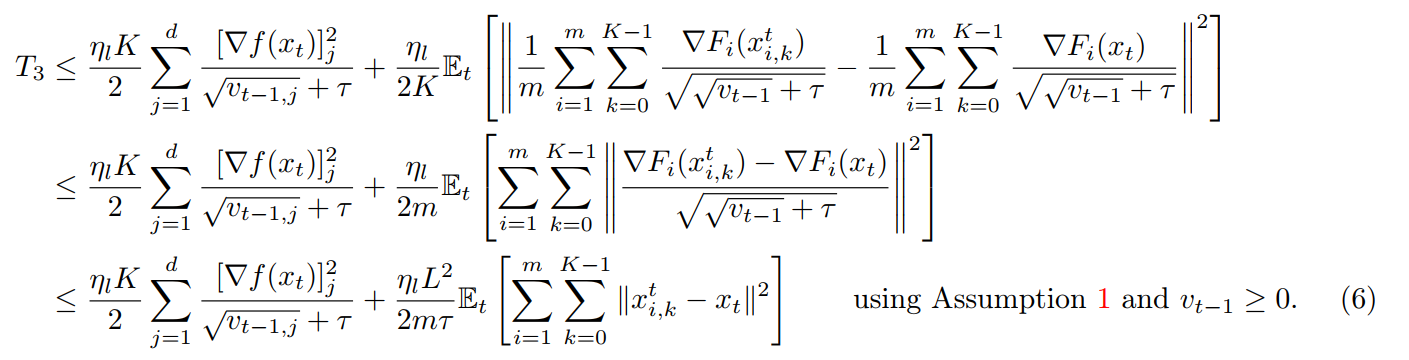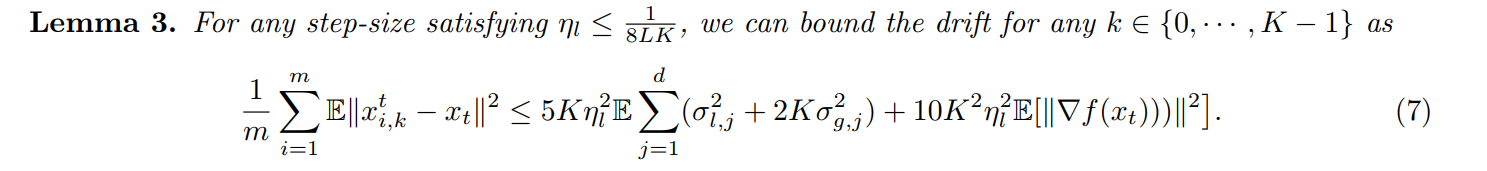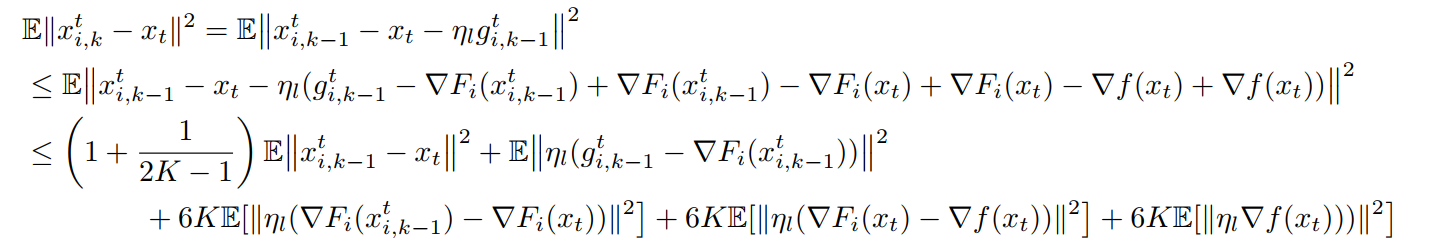论文笔记(2)—"Adaptive Federated Optimization"

Intuition

Authors demonstrated that the gap between centralized and federated performance was caused by two reasons: 1)client drift, 2) a lack of adaptive.

Different from variance reduction methods, they extended federated learning with adaptive methods, like adam.

They rewrote the update rule of FedAvg

[x_{t+1}=x_t-frac{1}{vert mathcal Svert}sum_{iinmathcal S}(x_t-x_i^t) ]

Let (Delta_i^t=x_{i}^t-x_t), where (x_i^t) denotes the model of client (i) after local training.

The server learning rate (eta) is FedAvg is (1) with applying SGD and (Delta_i^t) is a kind of pseudo-gradient. They purposed that apart from SGD, the server optimizer could utilize adaptive methods to update server model (x). Their framework is following:

Convergence

Multi steps local update, concretely, (E[Delta_i^t] eq K abla F(x^t))), obstacles the analysis of convergence. In my opinion, they offered a roughly bound of error.

I'll only give my personal analysis of their proof of Theorem 1 and thoughts of Theorem 2 are similar.

Firstly, we should build relationships between (x^{t+1}) and (x^t). According to the update rule of adaptive methods and (L)-smooth assumption, we have

Furthermore, like in Adagrad, we will have

Now, we should bound these two terms (T_1) and (T_2)

So far, there is no local training involving (T_2) and we follow the same process of Adagrad

To bound (T_1), they tried to link (Delta_t) containing local update with ( abla f(x_t)).

As mentioned above, (Delta_t) is a kind of pseudo-gradient of ( abla f(x_t))

Again, note that (x_{i, k}) is (k)-th model during local training in client (i) and (x_t) is the server model at round (t).

In my opinion, how to bound (x_{i,k}^t-x_t) is the most impressive part of the whole paper.

Honestly, local gradient (g_{i,k}^t) builds the bridge between (x_{i, k}^t) and (x_t) and (E[ abla F_i(x_{i, k-1}^t)] eq abla F_i(x_t))

The second inequity is very rough and unclear. Known (E[eta_l(cdots))They used (E[Vert z_1+z_2+dots+z_rVert^2]leq rE[Vert z_1Vert^2+Vert z_2Vert^2]+dots+Vert z_rVert^2])