JZOJ6423. 【NOIP2019模拟11.11】画

Description

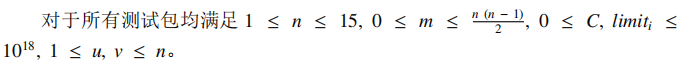
Solution

• NOIP前做NOI模拟？？？（神奇的题目）
• DP+DP+DP???
• 首先肯定是考虑如果没有边的限制怎么做啦。
  有一种显然的做法是数位DP，记一个状态S表示哪些顶住了上限。
  但是这样最优是只能做到64*3ⁿ的。
• 我们没有运用上异或的性质。还有一种更优的做法，枚举二进制下的一个位置表示在这个位置以上的所有位置所有点都顶住了上限（显然要先满足前面这些位置异或与C一样）。
  那么只要这个位置有一个没有顶住上限，下面的位置不管怎么选，这个位置都能将它变成C。
  记一个f[i][0/1][0/1]表示到i这个点，之前是否有点没有顶住上限，当前这一位的异或为0/1
  注意第一个没有顶住上限的点的贡献为1，其他的就是在满足当前条件下随便选的方案数。
• 这样的时间复杂度是O(64n)的。
• 现在我们考虑对所有边容斥。暴力枚举哪些条边的限制没有满足，根据二项式反演得到最终答案为$sum_{E'是E子集}(-1)^{|E'|}*(同一连通块内点的值相等后的答案)$。
• 由于各个连通块的贡献是单独算的，所以只需要计算单个连通块的贡献就好了。
• 设$G[S]$表示S这个连通块的容斥系数。容斥计算这个连通块联通就好了（任意选-不连通，枚举编号最小的点所在的连通块，剩下的边随便选）
  二项式反演得到在$E$中随便选的方案实际上是$[|E|=0]$
• 最后把它们合起来。如果连通块大小为偶数，那么就是0，大小为奇数才用计算最开始的F。
• 每一次合一个连通块进来，对于每一个连通块参与最后F的贡献的只有最小的点。用一个$3^n$的状态记录。枚举子集的时间用等比数列求和可以算出是$3^n$的。

---

• 刚开始边集算错了Orz，然后又没有考虑偶数块的贡献，对于奇数块的又没有取最小的（没有排序）
• 一大堆细节调了我一个上午cao。。。

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define maxn 16
#define maxm 15000000
#define ll long long 
#define mo 998244353
#define I(x,i) ((x&(1ll<<i))>0)
using namespace std;

int n,m,S,i,j,k,l,a[maxn][maxn],E[1<<maxn],nm[1<<maxn];
int _3[maxn],bt[1<<maxn],cnt[1<<maxn],pi[maxn];
ll C,lim[maxn],tmp[maxn],f[maxn][2][2],G[1<<maxn],F[1<<maxn],H[maxm];
ll Mi[1<<maxn];

int cmp(int i,int j){return lim[i]<lim[j];}

ll Las(ll X,int k){
	if (k<0) return 0;
	return X&((1ll<<k)-1);
}
ll P2(int k){
	if (k<0) return 0;
	return 1ll<<k;
}

ll DP(int S){
	int cnt=0,L=0; ll xs,sum=0,F;
	for(i=1;i<=n;i++) if (S&(1<<i-1)) tmp[++cnt]=lim[i];
	for(i=1;i<=n;i++) if (S&(1<<i-1))
		for(j=i+1;j<=n;j++) if (S&(1<<j-1))
			E[S]+=a[i][j];
	int cnt0=0; for(ll x=C;x;x>>=1) cnt0++; L=max(L,cnt0-1);
	for(i=1;i<=cnt;i++){
		cnt0=0; for(ll x=tmp[i];x;x>>=1) cnt0++; L=max(L,cnt0-1);
	}
	for(k=L+1;k>=0;k--){
		xs=0;
		for(i=1;i<=cnt;i++) xs^=tmp[i]>>k<<k;
		if (xs!=(C>>k<<k)) break;
		if (!k) {sum++;break;}
		memset(f,0,sizeof(f));
		f[0][0][0]=1;
		for(i=1;i<=cnt;i++) {
			int p=I(tmp[i],k-1);
			for(j=0;j<2;j++) for(l=0;l<2;l++) if (f[i-1][j][l])
				for(int now=0;now<=p;now++){
					if (now==p) F=Las(tmp[i],k-1)+1; else F=P2(k-1);
					if (!F) F++; F%=mo;
					if (j==0&&now<p) F=1;
					(f[i][j|now<p][l^now]+=f[i-1][j][l]*F%mo)%=mo;
				}
		}
		sum+=f[cnt][1][I(C,k-1)];
	}
	return sum%mo;
}

void dg(int i,int S,int T){
	if (i>n){
		if (S!=T&&E[T-S]==0) 
			G[T]=(G[T]-G[S]+mo)%mo;
		return;
	}
	if (I(T,i)) dg(i+1,S|(1<<i),T);
	dg(i+1,S,T);
}

void dg1(int i,int S,int T,int T0,int fir){
	if (i>n){
		if (!T0) return;
		if (!H[S]) return;
		ll Add=1;
		if (!(cnt[T0]&1)) T+=_3[fir-1],Add=(Mi[T0]+1)%mo;
		if (fir&&H[S]) 
			(H[T]+=H[S]*G[T0]%mo*Add%mo)%=mo;
		return;
	}
	if (!fir) {
		dg1(i+1,S,T+_3[i-1],T0|(1<<i-1),i);
		dg1(i+1,S+_3[i-1],T+_3[i-1],T0,fir);
		dg1(i+1,S+_3[i-1]*2,T+_3[i-1]*2,T0,fir);
	} else {
		dg1(i+1,S,T,T0,fir);
		dg1(i+1,S,T+_3[i-1]*2,T0|(1<<i-1),fir);
		dg1(i+1,S+_3[i-1]*2,T+_3[i-1]*2,T0,fir);
	}
}

int main(){
	scanf("%d%d%lld",&n,&m,&C);
	for(i=1;i<=n;i++) scanf("%lld",&lim[i]),pi[i]=i;
	sort(pi+1,pi+1+n,cmp);
	memcpy(tmp,lim,sizeof(tmp));
	for(i=1;i<=n;i++) lim[i]=tmp[pi[i]];
	for(i=1;i<=m;i++) {
		scanf("%d%d",&j,&k);
		for(int jj=1;jj<=n;jj++) if (pi[jj]==j)
			for(int kk=1;kk<=n;kk++) if (pi[kk]==k)
				a[jj][kk]=a[kk][jj]=1;
	}
	F[0]=C==0; for(S=1;S<1<<n;S++) F[S]=DP(S);
	for(i=0;i<=n;i++) bt[1<<i]=i;
	_3[0]=1; 
	for(i=1;i<=n;i++) _3[i]=_3[i-1]*3;
	for(S=1;S<1<<n;S++) {
		cnt[S]=cnt[S-(S&-S)]+1;
		if (cnt[S]==1) Mi[S]=lim[bt[S]+1];
		else Mi[S]=min(Mi[S-(S&-S)],lim[bt[S&-S]+1]);
		G[S]=E[S]==0;
		dg(bt[S&-S]+1,S&-S,S);
	}
	H[0]=1;
	dg1(1,0,0,0,0);
	ll ans=0;
	for(S=0;S<1<<n;S++){
		int T=0;
		for(i=1;i<=n;i++) if (S&(1<<i-1)) T+=_3[i-1];
			else T+=_3[i-1]*2;
		ans+=H[T]*F[S]%mo;
	}
	printf("%lld",ans%mo);
}