burnside定理学习小计

基本概念

• 置换：对一个集合的映射，简单来说就是重排列。
  一个集合$S$经过映射$a[1..n]$后得到$S'$的即$S'[1]=S[a[1]],S'[2]=S[a[2]]....$
• 不动点：如果一个集合$S$在通过置换$a$后生成的$S'$与$S$完全相同，那么我们就称$S$为$a$的不动点。
• 置换群（这个知识目前我没有用过）：置换群就是置换组成的集合，需要满足：
  

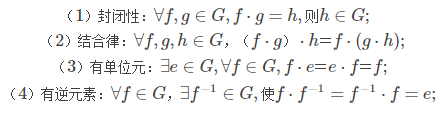
Burnside定理

• 集合$S$和$S'$是等价类当且仅当有一种置换群$G$中有置换$a$可以由$S$转变为$S'$.
• 对于一个圆环的染色方案就相当于是循环同构。
• 设$c_a$为置换$a$的不动点的个数,$L$为等价类个数。burnside引理就是
  $L=frac{c_{a_1}+c_{a2}+c_{a3}+...+c_{ag}}{|G|}$
• 看下面的例子以更好地理解。

圆环染色

• 对于一个大小为$n$的圆环，有$m$种颜色，问本质不同的染色方案有多少种。即循环同构的算一种。
• 对于一个圆环，有$n$种置换，构成一个置换群，即向右旋转1步，2步…n步。
• 那么对于第i种置换，我们要计算它的不动点的个数。
• 如果在向右旋转i步后完全一样的话，那么从0开始往后跳i步（0~n-1编号），最后会跳回0，这条路径上的所有位置的颜色都相同。
• 我们可以知道从0开始走多少步后就回来了。
  $x*iequiv 0: (mod :n) ->xequiv 0(mod:n/gcd(i,n))$.
• 即$n/gcd(i,n)$后回来，那么就一共有$gcd(i,n)$个环，每一个环里面的所有位置的颜色都是一样的。
• 那么对于不动点的个数就显而易见了：$m^{gcd(i,n)}$。
• 实际上这个就是polya定理

理解or证明

• 考虑一个染色方案被重复算了多少次。
• 一个长度为n的染色方案，它的循环节为c，那么当跳的步数为c的倍数时，这种染色方案就是不动点，共n/c次计算。
• 再考虑这个染色方案一共有c种循环同构的情况
  例如[abc][abc][abc]，[bca][bca][bca]，[cab][cab][cab]。
  这些在不考虑同构的情况下是都会被算到的。
• 所以一共算了n次。
• 所以最后要除以n。

JZOJ4800.周末晚会

传送门
N个人围绕着圆桌坐着，其中一些是男孩，另一些是女孩。你的任务是找出所有合法的方案数，使得不超过K个女孩座位是连续的。循环同构被视作同一种方案。

• 如果没有k的限制的话，那么就是burnside的模型。
• 注意到计算不动点的时候只用考虑到第一个循环节。
• 按照k和循环节大小分类讨论即可。
• DP计算f[i]，表示长度为i，没有多于连续k个的女孩，简单容斥一下
  $f[i]=f[i-1]*2-f[i-k-2]$
• d=循环节大小，首先对于每一个循环节要满足没有多于k个，其次考虑收尾相连，枚举相连的部分有多少个女孩，剩下的用f计算即可。

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define maxn 2005
#define ll long long
#define mo 100000007
using namespace std;

int T,n,k,i,j,d;
ll f[maxn],sum;

int gcd(int x,int y){return (x%y==0)?y:gcd(y,x%y);}
ll ksm(ll x,ll y){
	ll s=1;
	for(;y;y/=2,x=x*x%mo) if (y&1)
		s=s*x%mo;
	return s;
}

int main(){
	scanf("%d",&T);
	while (T--){
		scanf("%d%d",&n,&k);
		if (k>=n) {
			sum=0;
			for(i=1;i<=n;i++) sum+=ksm(2,gcd(i,n));
			sum%=mo;
			printf("%lld
",sum*ksm(n,mo-2)%mo);
			continue;
		}
		memset(f,0,sizeof(f));
		for(f[0]=1,i=1;i<=k;i++) f[i]=f[i-1]*2%mo;
		for(i=k+1;i<=n;i++) f[i]=(f[i-1]*2-((i==k+1)?1:f[i-k-2]))%mo;
		sum=0;
		for(i=1;i<=n;i++){
			d=gcd(i,n);
			if (d<=k) {sum+=ksm(2,d)-1;continue;}
			sum+=f[d];
			for(j=k+1;j<d&&j<=2*k;j++) 
				sum-=((d-j<=2)?1:f[d-j-2])*(k-(j-k)+1)%mo;
		}
		printf("%lld
",(sum%mo+mo)%mo*ksm(n,mo-2)%mo);
	}
}

牛客挑战赛34 C.远山的占卜

传送门
给2n的圆环染色，一共有m种颜色，循环同构以及对角线位置（即i与i+n）交换后相同的方案视为一种。
共有多少种不同的方案？
T(T<=2222)组数据,n,m<19260817，模19260817

• 将对角线的两个元素一起看的，那么一共有m*(m+1)/2种颜色，要涂到n个地方。
• 由于数据比较多，可以枚举gcd，然后乘phi(n/gcd)即可。

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define maxn 20000000
#define mo 19260817
#define ll long long 
using namespace std;

int T,i,j,k;
int tot,pri[maxn/10],bz[maxn],phi[maxn];
ll n,m,sum;

ll ksm(ll x,ll y){
	ll s=1;
	for(;y;y/=2,x=x*x%mo) if (y&1)
		s=s*x%mo;
	return s;
}

void GetPhi(){
	phi[1]=1;
	for(i=2;i<maxn;i++){
		if (!bz[i]) pri[++tot]=i,phi[i]=i-1;
		for(j=1;j<=tot&&i*pri[j]<maxn;j++) {
			bz[i*pri[j]]=1;
			if (i%pri[j]==0){
				phi[i*pri[j]]=phi[i]*pri[j]%mo;
				break;
			} else phi[i*pri[j]]=phi[i]*(pri[j]-1)%mo;
		}
	}
}

int main(){
	GetPhi();
	scanf("%d",&T);
	while (T--){
		scanf("%lld%lld",&n,&m);
		m=m*(m+1)/2%mo;
		sum=0;
		for(i=1;i<=sqrt(n);i++) if (n%i==0){
			sum+=ksm(m,i)*phi[n/i]%mo;
			if (i*i!=n) sum+=ksm(m,n/i)*phi[i]%mo;
		}
		printf("%lld
",sum%mo*ksm(n,mo-2)%mo);
	}
}