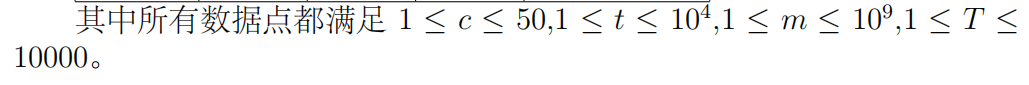Description
Solution
- n|xm-x等价于:任意p,满足 p|xm-x。p为质因子。
- 将n的质因子p分开考虑。
- 不难得出,在模p意义下满足以上条件的解y(y<p)。
- 那么我们要求最终解x同时满足所有质因子条件,每一个质因子都可以选择一些解y中的一个并且要求x与y在模p意义下同余,那么这个条件肯定满足了。如果cnti表示对于第i个质因子y的个数,那么共有cnt1* cnt2 * cnt3…*cntc种方案。
- 这样我们就可以得到其中一种方案的c条同余方程。
- 根据中国剩余定理,我们可以知道,在模M(M=所有模数即质因子的乘积,在这里就是n)下,这些同余方程有且只有一个解。
- 所以说一种同余方程的方案就对应着一个解。所以实际上解的个数就等于方案数cnt1* cnt2 * cnt3…*cntc。
- 求质因子内满足条件的个数等同于求所有xm%p (x<p) ,可以线性求过去,即用x的最小质因子去更新它,跟筛phi很像。
- 素数就直接快速幂。但是会被卡常,所以我们让m%(p-1),因为xp-1=1(mod p)
update 还有一种更秀的做法,碾爆正解
source%%%

我的辣鸡代码
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#define ll long long
#define mo 998244353
#define maxp 10005
using namespace std;
int id,T,c,m,mm,i,j,k,p;
int tot,pri[maxp],bz[maxp],f[maxp];
ll ans,cnt;
int ksm(int x,int y){
ll s=1;
for(;y;y/=2,x=x*x%p) if (y&1)
s=s*x%p;
return s;
}
int main(){
for(i=2;i<maxp;i++) {
if (!bz[i]) pri[++tot]=i;
for(j=1;j<=tot&&i*pri[j]<maxp;j++) {
bz[i*pri[j]]=i;
if (i%pri[j]==0) break;
}
}
scanf("%d",&id);
scanf("%d",&T);
while (T--){
scanf("%d%d",&c,&m);
ans=1;
while (c--){
scanf("%d",&p);
cnt=2,mm=m%(p-1);
for(i=2;i<p;i++) {
f[i]=bz[i]?f[bz[i]]*f[i/bz[i]]%p:ksm(i,mm);
cnt+=(f[i]==i);
}
ans=ans*cnt%mo;
}
printf("%lld
",ans);
}
}
数论大佬的做法
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#define ll long long
#define mo 998244353
#define maxp 10005
using namespace std;
int id,T,c,m,mm,i,j,k,p;
ll ans,cnt;
int gcd(int x,int y){
return (x%y==0)?y:gcd(y,x%y);
}
int main(){
scanf("%d",&id);
scanf("%d",&T);
while (T--){
scanf("%d%d",&c,&m);
ans=1;
while (c--){
scanf("%d",&p);
ans=1ll*ans*(gcd(m-1,p-1)+1)%mo;
}
printf("%lld
",ans);
}
}