先介绍两个数学定理。。。
同余
两个整数a、b,若它们除以整数m所得的余数相等,则称a与b对于模m同余或a同余于b模m。
记作:a≡b (mod m),
读作:a同余于b模m,或读作a与b对模m同余,例如26≡2(mod 12)。
定义
设m是大于1的正整数,a、b是整数,如果m|(a-b),则称a与b关于模m同余,记作a≡b(mod m),读作a与b对模m同余。
显然,有如下事实
(1)若a≡0(mod m),则m|a;
(2)a≡b(mod m)等价于a与b分别用m去除,余数相同。
证明
充分性:m|(a-b)→a≡b(mod m)。
设a=mq1+r1,b=mq2+r2,
且0≤r1,r2<m,
∵m |(a-b),
又a-b=m(q1-q2)+(r1-r2)。
∴必有常数n使得(r1-r2)=mn。
则有m|(r1-r2)。
∵0≤r1,r2<m,
∴0≤|r1-r2|<m,
∴r1-r2=0,
即r1=r2,故a≡b(mod m)。
必要性:a≡b(mod m)→m|(a-b)。
设a,b用m去除余数为r,
即a=mq1+r,b=mq2+r。
∵m(q1-q2)=(a-b),
∴m|(a-b)。
费马小定理
内容:如果p是一个质数,而整数a不是p的倍数,则有a^(p-1)≡1(mod p),所以有a^(p-2)=a-1
证明:
补充几个定义:
剩余系:对于一个特定整数n,一个整数集中所有数模n的余数集
完全剩余系:设m∈Z+,若r0,r1,...rm-1为m个整数,并且两两模m不同余,则r0,r1,...rm-1叫作模m的一个完全剩余系。
引理1.
若a,b,c为任意3个整数,m为正整数,且m与c互质,则当a·c≡b·c(mod m)时,有a≡b(mod m)。
证明:a·c≡b·c(mod m)可得ac–bc≡0(mod m)可得(a-b)·c≡0(mod m)。因为(m,c)=1即m,c互质,c可以约去,a– b≡0(mod m)可得a≡b(mod m)。
证明:a·c≡b·c(mod m)可得ac–bc≡0(mod m)可得(a-b)·c≡0(mod m)。因为(m,c)=1即m,c互质,c可以约去,a– b≡0(mod m)可得a≡b(mod m)。
引理2.
设m是一个整数且m>1,b是一个整数且m与b互质。如果a[1],a[2],a[3],a[4],…a[m]是模m的一个完全剩余系,则b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]也构成模m的一个完全剩余系。
证明:若存在2个整数b·a[i]和b·a[j]同余即b·a[i]≡b·a[j](mod m)..(i>=1 && j>=1),根据引理1则有a[i]≡a[j](mod m)。根据完全剩余系的定义可知这是不可能的,因此不存在2个整数b·a[i]和b·a[j]同余。
设m是一个整数且m>1,b是一个整数且m与b互质。如果a[1],a[2],a[3],a[4],…a[m]是模m的一个完全剩余系,则b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]也构成模m的一个完全剩余系。
证明:若存在2个整数b·a[i]和b·a[j]同余即b·a[i]≡b·a[j](mod m)..(i>=1 && j>=1),根据引理1则有a[i]≡a[j](mod m)。根据完全剩余系的定义可知这是不可能的,因此不存在2个整数b·a[i]和b·a[j]同余。
所以b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]构成模m的一个完全剩余系。
构造素数
 的完全剩余系
的完全剩余系
因为
 ,由引理2可得
,由引理2可得
也是p的一个完全剩余系。由完全剩余系的性质,
即

易知
 ,同余式两边可约去
,同余式两边可约去
 ,得到
,得到
这样就证明了费马小定理(摘自百度词条,仔细想想确实很好懂)
扩展欧几里得 (主要用于求解不定方程)
补充:欧几里得算法(辗转相除)
定义:对于已知a,b,必然存在ax+by=gcd(a,b)
证明:
由 ax+by=gcd(a,b) 得 bx1+(a%b)y1=gcd(b,a%b)
又∵a%b=a-[a/b]*b (此处[]为向下取整函数)
函数图像为:
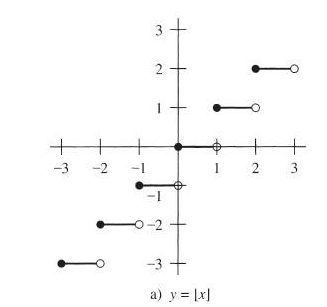
(会有用)
ax+by=bx1+(a-[a/b]*b)y1
化简为:
a(x-y1)=b(x1-y-[a/b]*y1)
解得
x=y1
y=x1-[a/b]*y1
从头递归求解就行。
怎样求逆元
扩展欧几里得
大概思路:
设a在模p意义下的逆元为x
则有 axΞ1(mod p)
∴ax=kp+1 (k为未知数)
∴ax-kp=1
利用扩展欧几里得求不定方程解就好
#include<iostream> using namespace std; void exgcd(int a,int b,int &x,int &y) { if(b==0) { x=1; y=0; return; } exgcd(b,a%b,y,x); y-=a/b*x; } int main() { int n,p; cin>>n>>p; int x,y; for(int i=1;i<=n;i++) { exgcd(i,p,x,y); x=(x%p+p)%p; cout<<x<<endl; } return 0; }
(长的跟想象中的不太一样,着重记一记)
费马小定理
大概思路:
∵a-1=a(p-2)
利用快速幂求解
#include<iostream> using namespace std; int fm(int a,int b,int p) { int base=a; int ans=1; while(b) { if(b&1) ans=(ans*base)%p; base=(base*base)%p; b=b/2; } return ans; } int main() { int n,p; cin>>n>>p; int p1=p-2; for(int i=1;i<=n;i++) { cout<<fm(i,p1,p)<<endl; } return 0; }
代码大概长这样
看一道题。。
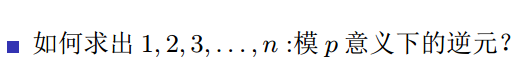
可以每个数直接调用上述的两种求逆元的方法,求解 时间复杂度O(nlogn)
还可以更优化一点,利用1,2,3,……n-1的逆元求n的逆元

(看不懂的话可以想一下模运算的加法原理)
(因为r小于i,所以r的逆元已知)
#include<iostream> #include<cstdio> using namespace std; long long int inv[3000003]; int main() { int n,p; cin>>n>>p; inv[1]=1; cout<<1<<endl; for(int i=2;i<=n;i++) { inv[i]=(long long int)(p-p/i)*inv[p%i]%p; printf("%d ",inv[i]); } return 0; }

这里解释一下为什么除以一个数的逆元等价于乘以它的逆元
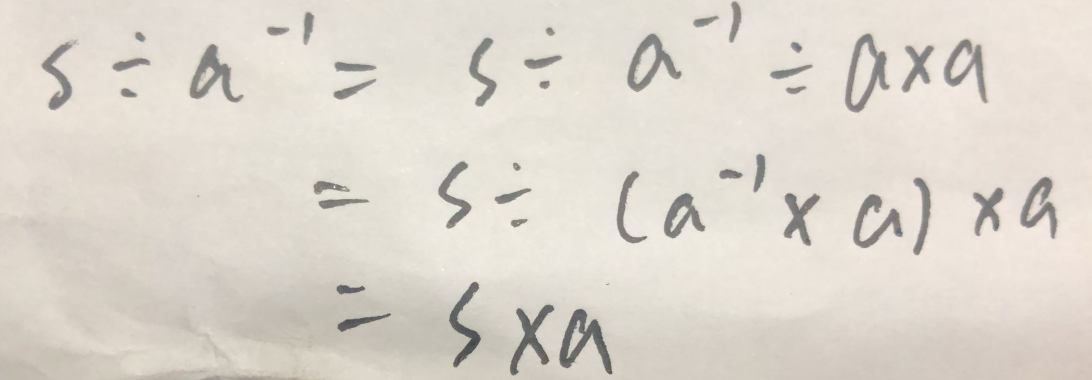
例题:

(自己思考!!!!)
提示:列不定方程求解
(RP++!)