T1:真的是简单的模拟,再简单不过了,其实就是求这个里面那个比值最小。
要注意他当前这个店也是要算在比较的范围内的。
#include <bits/stdc++.h>
using namespace std;
const int Inf=1<<30;
inline int read() {
int w=0,x=0; char ch=0;
while (!isdigit(ch)) {w|=ch=='-';ch=getchar();}
while (isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return w?-x:x;
}
double Max(double n,double m) {return n>m?n:m;}
double Min(double n,double m) {return n<m?n:m;}
int main() {
int xncs=read(),ynsc=read(),n=read();
double ans=(1.0*xncs)/(1.0*ynsc);
for (int i=1;i<=n;i++) ans=Min(1.0*read()/(1.0*read()),ans);
printf("%0.2lf
",ans*1000);
return 0;
}
T2:真的是简单的模拟,还是非常简单的。我是O(6^3)枚举全部的情况,然后在检查一下是否合法就可以了,要注意字典序要是最小的。
var
st:array[1..6]of string;
ans,tmp:string;
i,j,k:longint;
function check(x,y,z:longint):boolean;
var
map:array[1..3,1..3]of char;
vis:array[1..6]of boolean;
s:string;
fg:boolean;
i,j,k:longint;
begin
for i:=1 to 6 do vis[i]:=true; vis[x]:=false; vis[y]:=false; vis[z]:=false;
for i:=1 to 3 do map[1][i]:=st[x][i];
for i:=1 to 3 do map[2][i]:=st[y][i];
for i:=1 to 3 do map[3][i]:=st[z][i];
for i:=1 to 3 do
begin
s:=map[1][i]+map[2][i]+map[3][i];
fg:=false;
for j:=1 to 6 do
if (j<>x)and(j<>y)and(j<>z) then
if (vis[j])and(s=st[j]) then
begin
fg:=true;
vis[j]:=false;
break;
end;
if (fg=false) then exit(false);
end;
exit(true);
end;
begin
assign(input,'match.in'); reset(input);
assign(output,'match.out'); rewrite(output);
for i:=1 to 6 do readln(st[i]);
ans:='ZZZZZZZZZ';
for i:=1 to 6 do
for j:=1 to 6 do
begin
if (i=j) then continue;
for k:=1 to 6 do
begin
if (i=k)or(j=k) then continue;
tmp:=st[i]+st[j]+st[k];
if (check(i,j,k))and(ans>tmp) then ans:=tmp;
end;
end;
if (ans='ZZZZZZZZZ') then writeln(0)
else
begin
for i:=1 to 3 do
begin
for j:=1 to 3 do write(ans[(i-1)*3+j]);
writeln;
end;
end;
end.
T3:真的是卡特兰数,我们一般知道的推导公式是
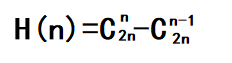
但是,卡特兰数是非常大的,这里是要%%%的,所以这个公式我们就用不了了。
所以我们要换一个公式:
f(n)=f(0)(n-1)+f(1)f(n-1)+...+f(n-1)*f(0)
这个公式因为是只是涉及到加法的公式,所以我们随便%%%。
那么就好了。(这道题做不出来,那么就是初赛没有好好复习)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL Mod=100000007;
inline int read() {
int w=0,x=0; char ch=0;
while (!isdigit(ch)) {w|=ch=='-';ch=getchar();}
while (isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return w?-x:x;
}
LL f[3005];
int main() {
freopen("cirs.in","r",stdin);
freopen("cirs.out","w",stdout);
int n=read();
f[1]=f[0]=1;
for (int i=2;i<=n;i++) {
for (int j=0;j<i;j++) {
f[i]=(f[i]+f[j]*f[i-j-1])%Mod;
}
}
printf("%lld
",f[n]);
return 0;
}
T4:真的是动态规划,不知道有没有看出来是背包,算了不管了。
我们需要知道两大核心,两大思路。
核心1:状态:F[i][j]表示第i辆车,人数为j的最少钱
核心2:状态转移方程:
我们参照一下背包:f[i][j]=max(f[i][j],f[i-1][j-w[i]]+v[i]);
滚动♂优化:f[j]=max(f[j],f[j-w[i]]+v[i]);
我们就可以参照一下这个思路,我们就考虑选和不选的情况
不选就是f[i-1][j],也就是这个车子是空的?Why?因为f[i][j]表示这个车i个人,j个人。但是f[i-1][j]有表示i-1辆车中有j个人,那么就是不是就是这个第i辆车是不是就是没有人了。
那么选的情况就是f[i-1][j-s]+d+sv
是不是这个意思,我们枚举一个s就可以了,表示的就是当前这个第i辆车的人数。
我们要求最小值,那么就去一个min可以了。
那么我们就滚动优化一下:f[j]=min(f[j],f[j-t]+d+ta)
好像是不是更优了一点QAQ!
#include <cstdio>
#include <cstring>
#include <ctype.h>
#include <algorithm>
using namespace std;
const int Inf=0x3f3f3f3f;
int n,k,d,s,a,b;
int f[105][105];
inline int read() {
int w=0,x=0;char ch=0;
while (!isdigit(ch)) {w|=ch=='-';ch=getchar();}
while (isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return w?-x:x;
}
int main() {
n=read(),k=read(),d=read(),s=read();
memset(f,Inf,sizeof(f));
f[0][0]=0;
for (int i=1;i<=k;i++) {
a=read(),b=read();
for (int j=0;j<=n;j++) {
f[i][j]=f[i-1][j];
for (int t=0;t<=b;t++) {
if (j>=t) f[i][j]=min(f[i][j],f[i-1][j-t]+d+t*a);
}
}
}
if (f[k][n]!=Inf) printf("%d
",f[k][n]);
else printf("impossible
");
return 0;
}
(滚动优化,还未测试)
#include <cstdio>
#include <cstring>
#include <ctype.h>
#include <algorithm>
using namespace std;
const int Inf=0x3f3f3f3f;
int n,k,d,s,a,b;
int f[105];
inline int read() {
int w=0,x=0;char ch=0;
while (!isdigit(ch)) {w|=ch=='-';ch=getchar();}
while (isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return w?-x:x;
}
int main() {
n=read(),k=read(),d=read(),s=read();
memset(f,Inf,sizeof(f));
f[0]=0;
for (int i=1;i<=k;i++) {
a=read(),b=read();
for (int j=0;j<=n;j++) {
for (int t=b;t>=0;t--) {
if (j>=t) f[j]=min(f[j],f[j-t]+d+t*a);
}
}
}
if (f[k]!=Inf) printf("%d
",f[k]);
else printf("impossible
");
return 0;
}