《背包九讲》 阅读笔记

《背包九讲》 阅读笔记

​ 背包问题是动态规划中非常经典的问题，其题目大致描述为：有N件物品和一个容量为V的背包，第 i 件物品的体积为 c[i]， 价值为 w[i]。求解如何装入可使背包中物品价值最大。

一、01背包

1. 基本思路：

​ 01背包表示这N件物品每个都只能拿0次或者1次。01背包是所有背包问题的基石。设F[i, v] 表示从前 i 件物品中选择一些放入容量为 v 背包所能得到的最大价值，那么可以得到状态转移方程为：

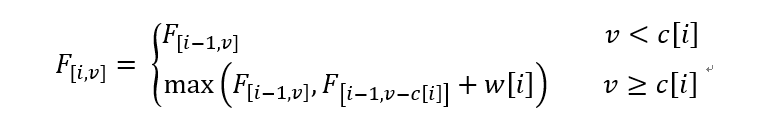
​ 在第 i 件物品体积 c[i] 没有超过背包容量 v 的情况下，要考虑的就是第 i 件物品放与不放的情况。若不放就转化为前 i-1 件物品放入容量 v 背包所能取得的最大价值；若放就转化为前 i-1 件物品放入 容量 v - c[i] 背包所能取得的最大价值加上第 i 件物品价值w[i]。

​ 边界条件为：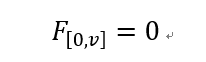

​ 这样，创建二维数组F，逐行计算后，F[N, V] 即为所求。

2. 优化思路：但可以注意到，每次计算的结果仅依赖于上一行的当前列和左侧某列两个元素，并且最终结果是最后一行的最后一个元素，所以只需要创建一个一维数组，计算每行时从后往前覆盖，将空间复杂度优化为 O(V)，伪代码为：

   for i=1..N
       for v=V..0
           f[v]=max{f[v],f[v-c[i]]+w[i]};
   

二、完全背包

​ 完全背包表示这 N 个物品每个可以拿无数次。完全背包有两种思路：

1. 基本思路：由于背包容量的限制，每种物品其实最多拿 n[i] = V / c[i] 次，将这 n[i] 个物品展开，其实就形成了一个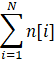的01背包，因为01背包问题本身其实没有限制 N 件物品必须不同。

   优化：

   ​ a. 每件物品都可以拿多次，那么我们可以只要那些“物美价廉”的物品，即如果一个物品比其他所有相同体积的物品价值都要高或者同价值但体积最小，就可以将其他物品排除不做考虑。

   ​ b. 第 i 个物品不用展开为 n[i] 个，而是 1 2 4 .. 2^k k = 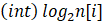个体积和价值都为原来 2^k 倍的物品，这样不管是取多少个，都可以由这些合并而来，于是优化为了一个 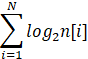的01背包。

2. 优化思路：不用转化为完全背包，对于第 i 件物品分为一件都不取和至少取一件两种情况讨论，于是状态转移方程为

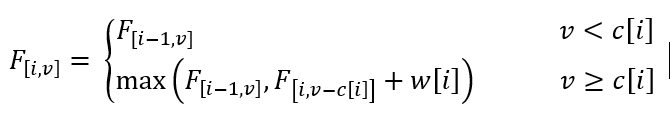
边界条件与 01 背包时相同

做空间复杂度优化时，可以注意到二维数组元素的计算仅依赖于上一行的当前列和当前行的左侧某列两个元素，所以创建一个一维数组，计算时从前往后覆盖写，最后代码刚好和01背包仅在 v 的循环顺序上相反，伪代码如下

for i=1..N
    for v=0..V
    	f[v]=max{f[v],f[v-c[i]]+w[i]};

三、多重背包

​ 多重背包限制第 i 件商品最多拿 m[i] 个

1. 基本思路：同样是将 m[i] 个物品展开，最后变成一个01背包问题，同样可以使用完全背包中的 1.b 的优化。
2. 优化思路：对于 m[i] * c[i] >= V 的物品实际上等同于无限，对于这些物品可以不用展开，当作无线背包物品处理即可，即在内层循环时 v 从 0 到 V。

四、混合背包

​ 混合背包即有的物品只有一次，有的无限次，有的限制 m[i] 次。

​ 如果是01背包和完全背包的混合，那么处理时只需要对不同类型的物品在内存循环时分别采用正序和倒序即可，伪代码为

for i=1..N
    if 第i件物品是01背包
        for v=V..0
      		f[v]=max{f[v],f[v-c[i]]+w[i]};
    else if 第i件物品是完全背包
        for v=0..V
	        f[v]=max{f[v],f[v-c[i]]+w[i]};

​ 如果混入了多重背包，按照多重背包的思路处理即可。

五、二维费用背包

​ 二维费用背包，即背包有两个维度的限制。如重量和容量，第 i 件物品的重量为 h[i]，背包最大承重 B。熟悉了二维背包也就熟悉了N维背包。

1. 基本思路：如果是01背包限制多了一维，那么状态也对应多一维即可，此时状态转移方程为：

   

2. 优化思路:同样是对空间复杂度进行优化,使用一个二维数组存储状态。

六、分组背包

​ 分组背包是指这 N 件物品被分为 K 组，每个组只能取其中一个物品。

1. 基本思路：使用 F[k, v] 表示，从前 k 组取物品，背包容量为 v 情况下背包所能装下的最大价值。那么解决的思路同样是考虑当前组不取和当前组取一个(需要进行比较，选出可取出的最大价值)，状态转移方程为：

   

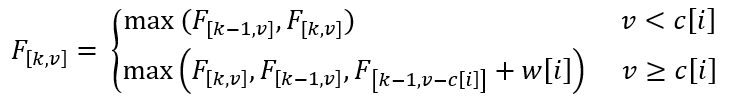
   边界条件为：F[0,v] = 0 ，伪代码为

   for 所有的组k
       for v=V..0
           for 所有的i属于组k
           	f[k][v]=max{f[k][v],f[k-1][v],f[k-1][v-c[i]]+w[i]}
   

2. 优化思路：同样是在空间复杂度上进行优化，但要额外注意的是使用二维数组存储状态时 v 和 i 的循环先后可以调换，而使用一维数组存储状态时循环必须是先 v 后 i，原因是对于一个 v 要从该组所有的 i 中选出最优的一个才能进行下一个元素的计算，否则同组之间元素将相互影响，具体代码可以参考：分组背包循环顺序对结果的影响， 伪代码为：

   for 所有的组k
       for v=V..0
           for 所有的i属于组k
           	f[v]=max{f[v],f[v-c[i]]+w[i]}
   

七、其他

​ 对于有依赖的背包问题和泛化物品力有未逮，不在此记录。

​ leetcode的背包问题：

​ 01背包：494. 目标和、416. 分割等和子集、1049. 最后一块石头的重量 II

​ 完全背包：322. 零钱兑换、279. 完全平方数、518. 零钱兑换 II、377. 组合总和 Ⅳ

​ 多维背包：474. 一和零、879. 盈利计划

​ 分组背包：1155. 掷骰子的N种方法

​

参考资料

- [1] 背包九讲第二版
- [2] dd大牛的《背包九讲