题目

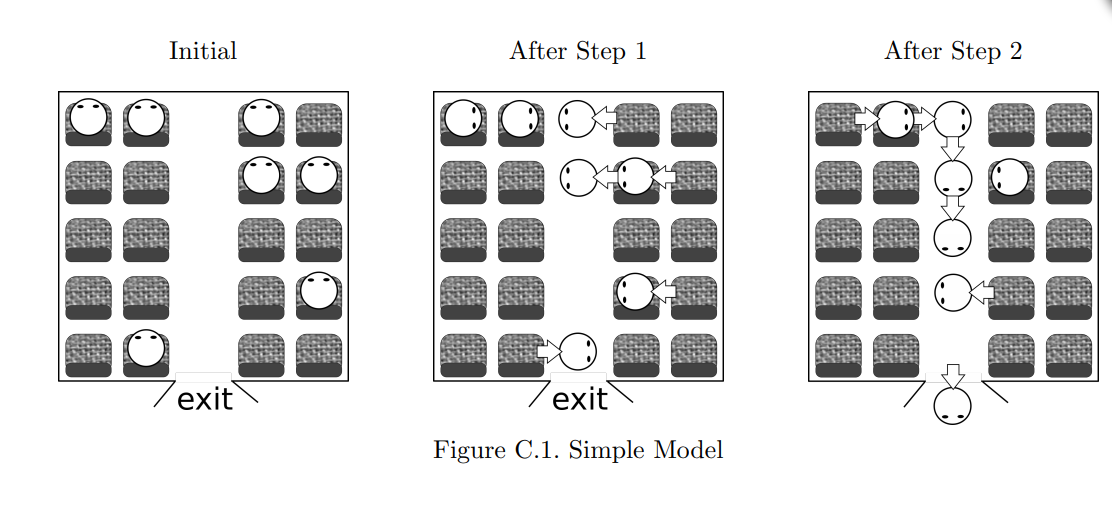


解说
大致题意:给出列数、两边行数和人数,求把所有人挪出来需要的时间。一个位置上一次只能存在一个人。
如果没有人和人之间的相互阻碍的话这道题极其简单,所以现在的主要问题就落在了如何处理人挡人的问题。
什么情况下会出现人挡人呢?显然是两个人到出口的时间一样的时候。
由于这个结论可能没那么显然,所以下面给一个通俗的证明解说。

比如画圈的两个人在没人遮挡时出去的时间是一样的,两人到最后肯定都要经过出口前的一段路,这一段就是公共部分(蓝色)。由于两人时间相等,因此刨去公共时间后的各自的时间(红色和绿色)也是相等的,也就是说两人在相等的时间后走到了重叠路段上,因此两人一定相遇。这样的话如果有两个人的距离相等就说明需要等待,那么我们给第二个人的时间加1,给第三个人的时间加2,以此类推即可。
既然这样事情就简单了。把所有距离由小到大排序,之后按上面的方法操作即可。
然后就有了我的第一代代码:
(下面展示核心部分)
1 for(int i=1;i<=p;i++){ 2 if(a[i]==a[i-1]) k[i]=k[i-1]+1; 3 a[i]+=k[i]; 4 ans=max(ans,a[i]); 5 }
然后就WA了。
(啊啊啊不可能我这么难得地进行了这么严谨的论证怎么可能出错???大脑在颤抖!!!)
哪里出问题了呢?
仔细想一下会发现上面的代码没有考虑排在前面的时间增加后对后面的影响。设想一种情况:由于我们已经从小到大排了序,那么正常情况下前一个数小于等于后一个,但由于时间增加,前一个数有可能变得比后一个大,这种情况是什么意思?就是一个本来排在你前面的人由于延时时间变得比后面长了,也就是说后面的人被前面的堵住了,并且前面的人堵多长时间后面的就要陪它堵多长时间,因为后面的过不去啊。所以说我们在遍历数组时应判断前面的数是否大于等于后面的,若是,就把后面的数改为前面的数加1。
代码

1 #include<cstdio> 2 #include<algorithm> 3 #include<cmath> 4 using namespace std; 5 const int maxn=500000+5; 6 int a[maxn]; 7 int main(){ 8 int r,s,p; 9 scanf("%d%d%d",&r,&s,&p); 10 for(int i=1;i<=p;i++){ 11 int x,y; 12 scanf("%d%d",&x,&y); 13 if(y>s) a[i]=r-x+1+y-s; 14 else a[i]=r-x+1+s-y+1; 15 } 16 sort(a+1,a+1+p); 17 int ans=-1; 18 for(int i=1;i<=p;i++){ 19 ans=max(ans,a[i]); 20 if(a[i]>=a[i+1]) a[i+1]=a[i]+1; 21 } 22 printf("%d",ans); 23 return 0; 24 }
幸甚至哉,歌以咏志。
