Day 4
网络流的理论性知识(算了。。我自己都看不下去,还是整理些例题以后复习用吧qaq):
一、PPT(主要内容)
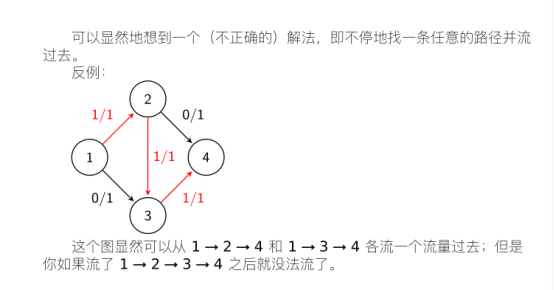

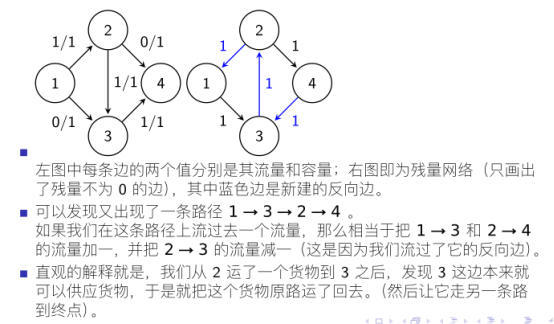



二、搜自度娘
定义:
①图论中的一种理论与方法,研究网络上的一类最优化问题 。1955年 ,T.E.哈里斯在研究铁路最大通量时首先提出在一个给定的网络上寻求两点间最大运输量的问题。1956年,L.R. 福特和 D.R. 富尔克森等人给出了解决这类问题的算法,从而建立了网络流理论。所谓网络或容量网络指的是一个连通的赋权有向图 D= (V、E、C) , 其中V 是该图的顶点集,E是有向边(即弧)集,C是弧上的容量。此外顶点集中包括一个起点和一个终点。网络上的流就是由起点流向终点的可行流,这是定义在网络上的非负函数,它一方面受到容量的限制,另一方面除去起点和终点以外,在所有中途点要求保持流入量和流出量是平衡的。如果把下图看作一个公路网,顶点v1…v6表示6座城镇,每条边上的权数表示两城镇间的公路长度。现在要问 :若从起点v1将物资运送到终点v6去 ,应选择那条路线才能使总运输距离最短?这样一类问题称为最短路问题 。 如果把上图看作一个输油管道网 , v1 表示发送点,v6表示接收点,其他点表示中转站 ,各边的权数表示该段管道的最大输送量。现在要问怎样安排输油线路才能使从v1到v6的总运输量为最大。这样的问题称为最大流问题。
②最大流理论是由福特和富尔克森于 1956 年创立的 ,他们指出最大流的流值等于最小割(截集)的容量这个重要的事实,并根据这一原理设计了用标号法求最大流的方法,后来又有人加以改进,使得求解最大流的方法更加丰富和完善 。最大流问题的研究密切了图论和运筹学,特别是与线性规划的联系,开辟了图论应用的新途径。
③假设G(V,E) 是一个有限的有向图,它的每条边(u,v)∈E都有一个非负值实数的容量c(u,v) 。如果(u,v)不属于E,我们假设c(u,v) = 0 。我们区别两个顶点:一个源点s和一个汇点t。一道网络流是一个对于所有结点u和v都有以下特性的实数函数f:V×V→R
|
(1)容量限制 |
(2)f(u,v)≤c(u,v)一条边的流不能超过它的容量。 |
|
(3)斜对称 |
(4)f(u,v)=-f(v,u)由u到v的净流必须是由v到u的净流的相反(参考例子)。(既然要看网络流,这是一定要知道的) |
|
(5)流守恒 |
(6)除非u=s或u=t,否则Σ(w∈V)f(u,w)=0 一结点的净流是零,除了"制造"流的源点和"消耗"流的汇点。 |
④注意f(u,v) 是由u到v的净流。如果该图代表一个实质的网络,由u到v有 4 单位的实际流及由v到u有 3 单位的实际流,那么f(u,v) = 1 及f(v,u) = − 1。
⑤边的剩余容量 (Residual Capacity)是cf(u,v) =c(u,v)−f(u,v)。这定义了以Gf(V,Ef)表示的剩余网络 (Residual Network),它显示可用的容量的多少。留意就算在原网络中由u到v没有边,在剩余网络乃可能有由u到v的边。因为相反方向的流抵消,减少由v到u的流等于增加由u到v的流。扩张路径 (Augmenting Path)是一条路径 (u1,u2...uk),而u1 =s、uk=t及cf(ui,ui+ 1) > 0,这表示沿这条路径传送更多流是可能的。
最大流算法:
1、augment path,直译为"增广路径",其思想大致如下:
①原有网络为G,设有一辅助图G',其定义为V(G') = V(G),E(G')初始值(也就是容量)与E(G)相同。每次操作时从Source点搜索出一条到Sink点的路径,然后将该路径上所有的容量减去该路径上容量的最小值,然后对路径上每一条边<u,v>添加或扩大反方向的容量,大小就是刚才减去的容量。一直到没有路为止。此时辅助图上的正向流就是最大流。
②我们很容易觉得这个算法会陷入死循环,但事实上不是这样的。我们只需要注意到每次网络中由Source到Sink的流都增加了,若容量都是整数,则这个算法必然会结束。
③寻找通路的时候可以用DFS,BFS最短路等算法。就这两者来说,BFS要比DFS快得多,但是编码量也会相应上一个数量级。
④增广路方法可以解决最大流问题,然而它有一个不可避免的缺陷,就是在极端情况下每次只能将流扩大1(假设容量、流为整数),这样会造成性能上的很大问题,解决这个问题有一个复杂得多的算法,就是预推进算法。
2、push label,直译为"预推进"算法。
3、压入与重标记(Push-Relabel)算法
除了用各种方法在剩余网络中不断找增广路(augmenting)的Ford-Fulkerson系的算法外,还有一种求最大流的算法被称为压入与重标记(Push-Relabel)算法。它的基本操作有:压入,作用于一条边,将边的始点的预流尽可能多的压向终点;重标记,作用于一个点,将它的高度(也就是label)设为所有邻接点的高度的最小值加一。Push-Relabel系的算法普遍要比Ford-Fulkerson系的算法快,但是缺点是相对难以理解。
Relabel-to-Front使用一个链表保存溢出顶点,用Discharge操作不断使溢出顶点不再溢出。Discharge的操作过程是:若找不到可被压入的临边,则重标记,否则对临边压入,直至点不再溢出。算法的主过程是:首先将源点出发的所有边充满,然后将除源和汇外的所有顶点保存在一个链表里,从链表头开始进行Discharge,如果完成后顶点的高度有所增加,则将这个顶点置于链表的头部,对下一个顶点开始Discharge。
Relabel-to-Front算法的时间复杂度是O(V^3),还有一个叫Highest Label Preflow Push的算法复杂度据说是O(V^2*E^0.5)。我研究了一下HLPP,感觉它和Relabel-to-Front本质上没有区别,因为Relabel-to-Front每次前移的都是高度最高的顶点,所以也相当于每次选择最高的标号进行更新。还有一个感觉也会很好实现的算法是使用队列维护溢出顶点,每次对pop出来的顶点discharge,出现了新的溢出顶点时入队。
Push-Relabel类的算法有一个名为gap heuristic的优化,就是当存在一个整数0<k<V,没有任何顶点满足h[v]=k时,对所有h[v]>k的顶点v做更新,若它小于V+1就置为V+1。
最小费用流算法:
一.Ford和Fulkerson迭加算法.
基本思路:把各条弧上单位流量的费用看成某种长度,用求解最短路问题的方法确定一条自V1至Vn的最短路;在将这条最短路作为可扩充路,用求解最大流问题的方法将其上的流量增至最大可能值;而这条最短路上的流量增加后,其上各条弧的单位流量的费用要重新确定,如此多次迭代,最终得到最小费用最大流.
二.迭加算法:
①给定目标流量F或∞,给定最小费用的初始可行流=0
② 若V(f)=F,停止,f为最小费用流;否则转(3).
③ 构造 相应的新的费用有向图W(fij),在W(fij)寻找Vs到Vt的最小费用有向路P(最短路),沿P增加流f的流量直到F,转(2);若不存在从Vs到Vt的最小费用的有向路P,停止.f就是最小费用最大流.最大流问题仅注意网络流的流通能力,没有考虑流通的费用。实际上费用因素是很重要的。例如在交通运输问题中,往往要求在完成运输任务的前提下,寻求一个使总运输费用最省的运输方案,这就是最小费用流问题。如果只考虑单位货物的运输费用,那么这个问题就变成最短路问题。由此可见,最短路问题是最小费用流问题的基础。现已有一系列求最短路的成功方法。最小费用流(或最小费用最大流)问题 ,可以交替使用求解最大流和最短路两种方法,通过迭代得到解决。
三.二圈算法:
① 利用Ford和Fulkson标号算法找出流量为F(<=最大流)的流f.
②构造f对应的调整容量的流网络N'(f).
③ 搜索N'(f)中的负费用有向图C(Floyd算法),若没有则停止,否则转(4).
④在C上找出最大的循环流,并加到N上去,同时修改N'(F)中C的容量,转(3).
四. ZKW费用流:
①费用流是网络流的一个很重要的组成部分,也是非常有用的一种图论模型,关于费用流的算法,流传比较广的主要是消圈和增广路算法,而近来炒得沸沸扬扬的ZKW算法也是一种非常优秀的算法,这里我就谈谈我对此算法的一些理解。
②此算法是由ZKW大牛创立,主要思想仍然是找增广路,只是有了一些优化在里边。原来我们找增广路主要是依靠最短路算法,如SPFA。因此此算法的时间复杂度主要就取决于增广的次数和每次增广的耗费。由于每一次找增广路是都是重新算一遍,这样似乎显得有些浪费,如果我们能够缩短找增广路的时间,那必定会大大地优化算法。
③值得注意的是,在寻求最短路得过程中,设dis[i]为i到起点的距离,对于每一条由i引向j的边,必有dis[j]<=dis[i]+map[i][j];既然满足这样的恒等式,我们就可以借用KM算法的调整思想来寻求最短路,每次只走dis[j]=dis[i]+map[i][j]的路径,一旦不存在到达终点的路径,就扫描每一条边,找到最小的距离增加值,使得有至少一条新边被加入相等子图。
算法流程如下:
1.将dis数组清零,表示当前的相等子图内只有起点。(如果存在负权边,必须要用spfa跑一遍,初始化出dis数组,下面的第二题就是这样的例子)。
2.深搜,如果到达终点,全部回退更改流量,再进行步骤2;否则,转3。
3.修改dis的值,如果无法修改,结束程序,已经找到的答案,反之转2。
有上下界,v上面讨论的网络流都只对每条弧都限定了上界(其实其下界可以看成0),现在给每条弧<Vi, Vj>加上一个下界限制Aij (即必须满足 Aij≤fij)。v弧上数字对第一个是上界,第二个是下界。若是撇开下界不看,此图的最大流如图(a)所示,流量是6;但若是加入了下界的限制,它的最大流量就只有5了。
五、网络流的基本概念
例:现在想将一些物资从S运抵T,必须经过一些中转站。连接中转站的是公路,每条公路都有最大运载量。如下图:每条弧代表一条公路,弧上的数表示该公路的最大运载量。最多能将多少货物从S运抵T?
分析:
这是一个典型的网络流模型。若有向图G=(V,E)满足下列条件:① 有且仅有一个顶点S,它的入度为零,即d-(S) = 0,这个顶点S便称为源点,或称为发点。②有且仅有一个顶点T,它的出度为零,即d+(T) = 0,这个顶点T便称为汇点,或称为收点。③每一条弧都有非负数,叫做该边的容量。边(vi, vj)的容量用cij表示。则称之为网络流图,记为G = (V, E, C)
1.可行流
对于网络流图G,每一条弧(i,j)都给定一个非负数fij,这一组数满足下列三条件时称为这网络的可行流,用f表示它。(1) 每一条弧(i,j)有fij≤cij。(2) 除源点S和汇点T以外的所有的点vi,恒有:该等式说明中间点vi的流量守恒,输入与输出量相等。(3) 对于源点S和汇点T有:这里V(f)表示该可行流f的流量。
2.可改进路
给定一个可行流f=。若fij = cij,称<vi, vj>为饱和弧;否则称<vi, vj>为非饱和弧。若fij = 0,称<vi, vj>为零流弧;否则称<vi, vj>为非零流弧。定义一条道路P,起点是S、终点是T。把P上所有与P方向一致的弧定义为正向弧,正向弧的全体记为P+;把P上所有与P方向相悖的弧定义为反向弧,反向弧的全体记为P-。给定一个可行流f,P是从S到T的一条道路,如果满足:那么就称P是f的一条可改进路。(有些书上又称:可增广轨)之所以称作"可改进",是因为可改进路上弧的流量通过一定的规则修改,可以令整个流量放大。具体方法下一节会重点介绍,此不赘述。
定理:对于已知的网络流图,设任意一可行流为f,任意一割切为(U, W),必有:V(f) ≤ C(U, W)。通俗简明的讲:"最大流小于等于任意割"。这是"流理论"里最基础最重要的定理。整个"流"的理论系统都是在这个定理上建立起来的,必须特别重视。
六、求最大流
对可改进路P上的弧<vi, vj>,分为两种情况讨论:
①第一种情况:<vi, vj>∈P+,可以令fij增加一个常数delta。必须满足fij + delta ≤ cij,即delta ≤ cij – fij。
②第二种情况:<vi, vj>∈P-,可以令fij减少一个常数delta。必须满足fij - delta ≥ 0,即delta ≤ fij
根据以上分析可以得出delta的计算公式:因为P+的每条弧都是非饱和弧,P-的每条弧都是非零流弧,所以delta > 0。容易证明,按照如此规则修正流量,既可以使所有中间点都满足"流量守恒"(即输入量等于输出量),又可以使得总的流量有所增加(因为delta > 0)。
因此我们对于任意的可行流f,只要在f中能找到可改进路,那么必然可以将f改造成为流量更大的一个可行流。我们要求的是最大流,现在的问题是:倘若在f中找不到可改进路,f就一定是最大流。
定理1 可行流f是最大流的充分必要条件是:f中不存在可改进路。
证明:
首先证明必要性:已知最大流f,求证f中不存在可改进路。若最大流f中存在可改进路P,那么可以根据一定规则(详见上文)修改P中弧的流量。可以将f的流量放大,这与f是最大流矛盾。故必要性得证。再证明充分性:已知流f,并且f中不存在可改进路,求证f是最大流。我们定义顶点集合U, W如下:
(a) S∈U,
(b) 若x∈U,且fxy<cxy,则y∈U;若x∈U,且fyx>0,则y∈U。(这实际上就是可改进路的构造规则)
(c) W = V \ U。由于f中不存在可改进路,所以T∈W;又S∈U,所以U、W是一个割切(U, W)。按照U的定义,若x∈U,y∈W,则fxy = cxy。若x∈W,y∈U,则fxy = 0。又因 v(f)≤C(U,W)所以f是最大流。得证。
重要定理:最大流最小割定理:最大流等于最小割,即max V(f) = min C(U, W)。
求最大流的算法:
step 1. 令所有弧的流量为0,从而构造一个流量为0的可行流f(称作零流)。
step 2. 若f中找不到可改进路则转step 5;否则找到任意一条可改进路P。
step 3. 根据P求delta。
step 4. 以delta为改进量,更新可行流f。转step 2。
step 5. 算法结束。此时的f即为最大流。
七、最小费用最大流
1.问题的模型
流最重要的应用是尽可能多的分流物资,这也就是我们已经研究过的最大流问题。然而实际生活中,最大配置方案肯定不止一种,一旦有了选择的余地,费用的因素就自然参与到决策中来。
一般的,设有带费用的网络流图G = (V, E, C, W),每条弧<Vi, Vj>对应两个非负整数Cij、Wij,表示该弧的容量和费用。若流f满足:
(a) 流量V(f)最大。
(b) 满足a的前提下,流的费用Cost(f) = 最小。
就称f是网络流图G的最小费用最大流。
八、例题:
T1(P2756 飞行员配对方案问题):

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <queue> 5 #define inf 0x3f3f3f3f 6 using namespace std; 7 8 int n,m,s,t; 9 struct node { 10 int v,next,cap; 11 } e[6100]; 12 int head[6100],tot=1; 13 int dis[6100]; 14 15 void add_node(int a,int b,int c) { 16 e[++tot]=(node) {b,head[a],c}; 17 head[a]=tot; 18 } 19 20 bool bfs() { 21 memset(dis,-1,sizeof(dis)); 22 queue<int> q; 23 q.push(s); 24 dis[s]=0; 25 while(!q.empty()) { 26 int x=q.front(); 27 q.pop(); 28 for(int i=head[x]; i; i=e[i].next) { 29 int v=e[i].v; 30 if(e[i].cap&&dis[v]==-1) { 31 dis[v]=dis[x]+1; 32 q.push(v); 33 } 34 } 35 } 36 return dis[t]!=-1; 37 } 38 39 int dfs(int now,int f) { 40 if(now==t) return f; 41 int rest=f; 42 for(int i=head[now]; i; i=e[i].next) { 43 int v=e[i].v; 44 if(e[i].cap>0&&rest>0&&dis[v]==dis[now]+1) { 45 int t=dfs(v,min(rest,e[i].cap)); 46 if(!t) dis[v]=0; 47 e[i].cap-=t; 48 e[i^1].cap+=t; 49 rest-=t; 50 } 51 } 52 return f-rest; 53 } 54 55 void dinic() { 56 int ans=0; 57 while(bfs()) ans+=dfs(s,inf); 58 if(!ans) { 59 printf("No Solution!"); 60 return; 61 } 62 printf("%d\n",ans); 63 for(int i=2;i<=tot;i+=2) 64 { 65 int v=e[i].v; 66 int v1=e[i^1].v; 67 if(v==s||v1==s||v==t||v1==t) break; 68 if(e[i^1].cap!=0) 69 { 70 printf("%d %d\n",e[i^1].v,e[i].v); 71 } 72 } 73 } 74 75 int main() { 76 scanf("%d%d",&m,&n); 77 int x,y; 78 while(scanf("%d%d",&x,&y)==2) { 79 if(x==-1&&y==-1) break; 80 add_node(x,y,1); 81 add_node(y,x,0); 82 } 83 s=0;t=n+1; 84 for(int i=1; i<=m; ++i) { 85 add_node(s,i,1); 86 add_node(i,s,0); 87 } 88 for(int i=m+1; i<=n; ++i) { 89 add_node(i,t,1); 90 add_node(t,i,0); 91 } 92 dinic(); 93 }
T2(P2317 [HNOI2005]星际贸易):

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 #include<cstring> 6 using namespace std; 7 const int INF=0x3f3f3f3f; 8 typedef long long ll; 9 const int N=2005; 10 const int M=4005; 11 12 int dp[N][N],f[N][M],q[M][N]; 13 int n,m,s,t; 14 15 struct node { 16 int a,b,l,f,p; 17 }e[N*10]; 18 19 struct edge { 20 int h,z,c; 21 }a[M*10]; 22 23 inline int read() { 24 int n=0,f=1;char ch=getchar(); 25 while (ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();} 26 while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();} 27 return n*f; 28 } 29 30 inline void work_(int i,int j) { 31 if(e[i].p>0 && j>0) 32 f[i][j]=min(f[i][j],f[i][j-1]+e[i].p); 33 if(a[j+2].z>a[j+2].h) 34 f[i][j]=min(f[i][j],f[q[j+2][a[j+2].h]][j+2]+e[i].f); 35 if(a[i].c) a[j].h=a[j].z=0; 36 while(a[j].z>a[j].h && f[q[j][a[j].z-1]][j]>=f[i][j]) a[j].z--; 37 q[j][a[j].z++]=i; 38 while(a[j].h<a[j].z && e[i+1].l-e[q[j][a[j].h]].l>t) a[j].h++; 39 } 40 41 inline void init() { 42 n=read(),m=read(),s=read(),t=read(); 43 if(s>2*n) s=2*n; 44 for(int i=1;i<=n;++i) 45 e[i].a=read(),e[i].b=read(),e[i].l=read(),e[i].p=read(),e[i].f=read(); 46 } 47 48 int main(){ 49 init(); 50 for(int i=1;i<=n;i++) 51 if(e[i].l-e[i-1].l>t) { 52 printf("Poor Coke!"); 53 return 0; 54 } 55 memset(dp,-1,sizeof(dp)); 56 dp[0][0]=0; 57 for(int i=1;i<=n;++i) 58 for(int j=0;j<=m;++j){ 59 if(dp[i-1][j]>=0) dp[i][j]=dp[i-1][j]; 60 if(j>=e[i].a && dp[i-1][j-e[i].a]>=0) 61 dp[i][j]=max(dp[i][j],dp[i-1][j-e[i].a]+e[i].b); 62 } 63 int v=0; 64 for(int i=0;i<=m;i++) 65 if(dp[n][i]>dp[n][v]) v=i; 66 for(int i=n,j=v;i>=1;i--) 67 if(dp[i][j]==dp[i-1][j]) continue; 68 else a[i].c=true,j-=e[i].a; 69 memset(f,0x3f,sizeof(f)); 70 f[0][s]=0; 71 q[s][a[s].z++]=0; 72 for(int i=1;i<=n;i++) 73 for(int j=0;j<=s;j++) work_(i,j); 74 int u=0; 75 for(int i=0;i<=s;i++) 76 if(f[n][i]<f[n][u]) u=i; 77 if(f[n][u]==INF) printf("Poor Coke!"); 78 else printf("%d %d", dp[n][v], dp[n][v]-f[n][u]); 79 return 0; 80 } 81 /* 82 6 3 10 4 83 1 2 1 1 1 84 1 2 2 2 1 85 1 2 3 9 1 86 1 1 4 0 1 87 1 1 5 0 1 88 1 1 6 1 1 89 90 6 2 91 */
T3(P3324 [SDOI2015]星际战争):

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<queue> 5 #include<cstring> 6 #include<algorithm> 7 using namespace std; 8 typedef long long ll; 9 const int N=110; 10 int n,m,js; 11 int a[N],b[N],f[N][N],head[N],q[N]; 12 ll sum; 13 14 struct node{ 15 int to,nxt; 16 ll w; 17 }e[N*100];//改 18 19 inline ll read() { 20 ll n=0,f=1;char ch=getchar(); 21 while (ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();} 22 while (ch<='9'&&ch>='0') {n=n*10+ch-'0';ch=getchar();} 23 return n*f; 24 } 25 26 inline void add_(int x,int y,ll z) { 27 e[js].to=y; e[js].w=z; 28 e[js].nxt=head[x]; head[x]=js++;//js++,改(必须改) 29 e[js].to=x; e[js].w=0; 30 e[js].nxt=head[y]; head[y]=js++; 31 } 32 33 inline int bfs(int s,int t) { 34 memset(q,0,sizeof(q)); 35 queue <int > p; 36 q[s]=1; 37 p.push(s); 38 while (!p.empty()) { 39 int u=p.front(); 40 p.pop();//改 41 for(int i=head[u];i!=-1;i=e[i].nxt) {//改,循环是i!=-1 42 if(e[i].w>0 && !q[e[i].to]) { 43 q[e[i].to]=q[u]+1; 44 p.push(e[i].to); 45 } 46 } 47 } 48 return q[t]; 49 } 50 51 inline ll dfs(int v,int t,ll f) {//改,dfs最好不用inline 52 if(v==t) return f; 53 ll dz=0; 54 for(int i=head[v];i!=-1&&dz<f;i=e[i].nxt) {//改 55 if(e[i].w>0 && q[v]+1==q[e[i].to]) { 56 ll ans=dfs(e[i].to,t,min(e[i].w,f-dz)); 57 if(ans>0) { 58 e[i].w-=ans; 59 e[i^1].w+=ans; 60 dz+=ans; 61 } else { 62 q[e[i].to]=-1; 63 } 64 } 65 } 66 return dz; 67 } 68 69 inline ll dinic(int s,int t) { 70 ll flow=0; 71 while (bfs(s,t)) { 72 flow+=dfs(s,t,0x3f3f3f3f); 73 } 74 return flow; 75 } 76 77 bool check(ll t) { 78 memset(head,-1,sizeof(head)),js=0; 79 for(int i=1;i<=m;++i) add_(0,i,t*b[i]); 80 for(int i=1;i<=n;++i) add_(i+m,n+m+1,a[i]*10000); 81 for(int i=1;i<=m;++i) 82 for(int j=1;j<=n;++j) 83 if(f[i][j]) add_(i,j+m,0x3f3f3f3f);//少了一个3f 84 return dinic(0,n+m+1)==sum; 85 } 86 87 int main() { 88 n=read(),m=read(); 89 for(int i=1;i<=n;++i) { 90 a[i]=read(); 91 sum+=a[i]*10000; 92 } 93 for(int i=1;i<=m;++i) b[i]=read(); 94 for(int i=1;i<=m;++i) 95 for(int j=1;j<=n;++j) f[i][j]=read(); 96 int l=1,r=1000000000; 97 while (l<r) { 98 int mid=(l+r)>>1; 99 if (check(mid)) r=mid; 100 else l=mid+1; 101 } 102 printf("%.6f\n", r/10000.0); 103 return 0; 104 }
T4(P2472 [SCOI2007]蜥蜴):

1 #include<cstdio> 2 #include<cstring> 3 #include<cmath> 4 #include<iostream> 5 using namespace std; 6 const int inf=0x3f3f3f3f; 7 const int N=1010; 8 const int M=31; 9 10 int r,c,d,S,t,js=1,ans; 11 int b[N],f[M][M],head[N],dis[N],q[N*10]; 12 char s[M]; 13 14 struct node { 15 int v,nxt,cap; 16 }e[N*50]; 17 18 inline int read() { 19 int n=0,f=1;char ch=getchar(); 20 while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();} 21 while(ch>='0'&&ch<='9'){n=n*10+ch-'0';ch=getchar();} 22 return n*f; 23 } 24 25 inline void add(int x,int y,int cap) { 26 e[++js].v=y; e[js].cap=cap; 27 e[js].nxt=head[x]; head[x]=js; 28 e[++js].v=x; e[js].cap=0; 29 e[js].nxt=head[y]; head[y]=js; 30 } 31 32 inline int sqr(int x) { 33 return x*x; 34 } 35 36 inline double calc(int a,int b,int c,int d) { 37 return sqrt(sqr(a-c)+sqr(b-d)); 38 } 39 40 inline int pos(int x,int y,int add) { 41 return (x-1)*c+y+r*c*add; 42 } 43 44 inline bool pd(int x,int y) { 45 return x<=d||r-x<d||y<=d||c-y<d; 46 } 47 48 inline bool bfs() { 49 for(int i=S;i<=t;++i) dis[i]=inf; 50 int h=0,k=1; 51 q[k]=S,dis[S]=0; 52 while(h!=k){ 53 int x=q[++h]; 54 for(int i=head[x];i;i=e[i].nxt){ 55 int v=e[i].v; 56 if(e[i].cap && dis[v]>dis[x]+1){ 57 dis[v]=dis[x]+1; 58 if(v==t) return 1; 59 q[++k]=v; 60 } 61 } 62 } 63 return dis[t]<inf; 64 } 65 66 inline int dfs(int x,int f){ 67 if(x==t) return f; 68 int res=f; 69 for(int i=head[x];i;i=e[i].nxt){ 70 int v=e[i].v; 71 if(e[i].cap && dis[v]==dis[x]+1){ 72 int t=dfs(v,min(res,e[i].cap)); 73 if(!t) dis[v]=0; 74 e[i].cap-=t;e[i^1].cap+=t; 75 res-=t; 76 } 77 } 78 return f-res; 79 } 80 81 inline int dinic() { 82 int res=0; 83 while(bfs()) { 84 for(int i=S;i<=t;++i) b[i]=head[i]; 85 res+=dfs(S,inf); 86 } 87 return ans-res; 88 } 89 90 int main() { 91 r=read(),c=read(),d=read(); 92 S=0,t=2*r*c+1; 93 for(int i=1;i<=r;++i) { 94 scanf("%s",s+1); 95 for(int j=1;j<=c;++j) f[i][j]=s[j]-'0'; 96 } 97 for(int i=1;i<=r;++i) { 98 scanf("%s",s+1); 99 for(int j=1;j<=c;++j) 100 if(s[j]=='L') ans++,add(S,pos(i,j,0),1); 101 } 102 for(int i=1;i<=r;++i) 103 for(int j=1;j<=c;++j) 104 if(f[i][j]) add(pos(i,j,0),pos(i,j,1),f[i][j]); 105 for(int i=1;i<=r;i++) { 106 for(int j=1;j<=c;++j) { 107 if(!f[i][j]) continue; 108 for(int z=1;z<=r;z++) { 109 for(int o=1;o<=c;o++) { 110 if(i==z && j==o) continue; 111 if(f[z][o] && calc(i,j,z,o)<=d) 112 add(pos(i,j,1),pos(z,o,0),inf),add(pos(z,o,1),pos(i,j,0),inf); 113 } 114 } 115 } 116 } 117 for(int i=1;i<=r;++i) 118 for(int j=1;j<=c;++j) 119 if(pd(i,j)) add(pos(i,j,1),t,inf); 120 printf("%d",dinic()); 121 return 0; 122 }
T5(P4001 [BJOI2006]狼抓兔子):

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #include<queue> 7 using namespace std; 8 const int inf=0x3f3f3f3f; 9 const int N=2e6+10; 10 11 int n,m,s,t,res,ans,js=1; 12 int head[N],dis[N]; 13 14 struct node { 15 int v,nxt,cap; 16 }e[N*3]; 17 18 inline int read() { 19 int n=0,f=1;char ch=getchar(); 20 while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();} 21 while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();} 22 return n*f; 23 } 24 25 inline void add(int a,int b,int z) { 26 e[++js].v=b,e[js].nxt=head[a]; 27 e[js].cap=z,head[a]=js; 28 } 29 30 inline int bfs() { 31 memset(dis,-1,sizeof(dis)); 32 queue<int>q; 33 q.push(s); 34 dis[s]=0; 35 while (!q.empty()) { 36 int u=q.front(); 37 q.pop(); 38 for(int i=head[u];i;i=e[i].nxt) { 39 int v=e[i].v; 40 if(dis[v]==-1 && e[i].cap) { 41 dis[v]=dis[u]+1; 42 q.push(v); 43 } 44 } 45 } 46 return dis[t]!=-1; 47 } 48 49 inline int dfs(int p,int f) { 50 if(p==t) return f; 51 int w=f; 52 for(int i=head[p];i;i=e[i].nxt) { 53 int v=e[i].v; 54 if(w>0 && dis[v]==dis[p]+1 && e[i].cap>0) { 55 int t=dfs(v,min(w,e[i].cap)); 56 if(!t) dis[v]=0; 57 e[i].cap-=t,e[i^1].cap+=t,w-=t; 58 } 59 } 60 return f-w; 61 } 62 63 64 inline int dinic() { 65 int ans=0; 66 while(bfs()) ans+=dfs(s,inf); 67 return ans; 68 } 69 70 int main() { 71 n=read(),m=read(); 72 s=1,t=n*m; 73 int x; 74 for(int i=1;i<=n;++i) { 75 int jc=i*m-m; 76 for(int j=1;j<m;++j) { 77 x=read(); 78 add(jc+j,jc+j+1,x),add(jc+j+1,jc+j,x); 79 } 80 } 81 for(int i=1;i<n;++i) { 82 int jc=i*m-m; 83 for(int j=1;j<=m;++j) { 84 x=read(); 85 add(jc+j,jc+j+m,x),add(jc+j+m,jc+j,x); 86 } 87 } 88 for(int i=1;i<n;++i) { 89 int jc=i*m-m; 90 for(int j=1;j<m;++j) { 91 x=read(); 92 add(jc+j,jc+m+j+1,x),add(jc+m+1+j,jc+j,x); 93 } 94 } 95 res=dinic(); 96 printf("%d",res); 97 return 0; 98 }
T6(P2774 方格取数问题):

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<algorithm> 6 using namespace std; 7 typedef long long ll; 8 const int N=1001; 9 const int NN=90100; 10 const int maxn=10003; 11 const int maxm=80010; 12 13 int n,m,s,t,x,y,js=1,l,r,ax; 14 int a[N][N],head[NN],h[NN],q[NN]; 15 int fx[4][2]={{-1,0},{0,-1},{1,0},{0,1}}; 16 ll sum=0; 17 18 struct node{ 19 int to,w,nxt; 20 }e[NN]; 21 22 inline int read() { 23 int n=0,f=1;char ch=getchar(); 24 while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();} 25 while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();} 26 return n*f; 27 } 28 29 inline int calc(int x,int y) { 30 return (x-1)*m+y; 31 } 32 33 inline void add_edge(int x,int y,int z) { 34 e[++js].to=y; 35 e[js].w=z; 36 e[js].nxt=head[x]; 37 head[x]=js; 38 } 39 40 inline int bfs() { 41 memset(h,-1,sizeof(h)); 42 h[s]=1,l=0,r=1,q[r]=s; 43 while (l!=r) { 44 l++; 45 if(l==maxn) l=1; 46 int u=q[l]; 47 for(int i=head[u];i;i=e[i].nxt) { 48 int v=e[i].to; 49 if (h[v]==-1 && e[i].w>0) { 50 h[v]=h[u]+1,r++; 51 if(r==maxn) r=1; 52 q[r]=v; 53 } 54 } 55 } 56 return h[t]!=-1; 57 } 58 59 inline int dfs(int u,int s) { 60 if(u==t || s==0) return s; 61 int ansx=0,v,W; 62 for(int i=head[u];i;i=e[i].nxt) { 63 if(h[e[i].to]==h[u]+1) { 64 v=e[i].to; 65 W=dfs(v,min(e[i].w,s-ansx)); 66 ansx+=W,e[i].w-=W,e[i^1].w+=W; 67 if(ansx==s) return s; 68 } 69 } 70 if(ansx==0) h[u]=-1; 71 return ansx; 72 } 73 74 inline void work_(int i,int j) { 75 for(int k=0;k<4;k++) { 76 x=i+fx[k][0],y=j+fx[k][1]; 77 if(x<=0 || y<=0 || x>n || y>m) continue; 78 add_edge((i-1)*m+j,(x-1)*m+y,1e8),add_edge((x-1)*m+y,(i-1)*m+j,0); 79 } 80 } 81 82 inline int init() { 83 n=read(),m=read(); 84 s=n*m+1,t=n*m+2; 85 for(int i=1;i<=n;++i) { 86 for(int j=1;j<=m;++j) { 87 ax=read(); 88 sum+=ax; 89 if((i+j)%2==1) add_edge(s,(i-1)*m+j,ax),add_edge((i-1)*m+j,s,0); 90 else add_edge((i-1)*m+j,t,ax),add_edge(t,(i-1)*m+j,0); 91 } 92 } 93 } 94 95 int main() { 96 init(); 97 for(int i=1;i<=n;i++) 98 for(int j=1;j<=m;j++) 99 if((i+j)%2==1) work_(i,j); 100 while (bfs()) sum-=dfs(s,1e9); 101 printf("%lld\n",sum); 102 return 0; 103 } 104 /* 105 题目描述 106 在一个有 m*n 个方格的棋盘中,每个方格 107 中有一个正整数。现要从方格中取数,使任 108 意 2 个数所在方格没有公共边,且取出的数 109 的总和最大。试设计一个满足要求的取数算法 110 。对于给定的方格棋盘,按照取数要求编程找 111 出总和最大的数。 112 113 输入格式: 114 第 1 行有 2 个正整数 m 和 n,分别表示棋盘的行数和列数。 115 接下来的 m 行,每行有 n 个正整数,表示棋盘方格中的数。 116 117 输出格式: 118 程序运行结束时,将取数的最大总和输出 119 120 输入样例1: 121 3 3 122 1 2 3 123 3 2 3 124 2 3 1 125 126 输出样例1: 复制 127 11 128 129 */
T7(P3305 [SDOI2013]费用流):

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 using namespace std; 5 const int N=1e5+5; 6 int js=1,n,m,p,s,t,ans,x,y,z; 7 int head[N],dis[N],q[N],vis[N]; 8 double L,R; 9 10 struct edge { 11 int v,nxt; 12 double cap; 13 }e[N<<1]; 14 15 struct node { 16 int x,y; 17 double z; 18 }d[N]; 19 20 inline int read() { 21 int n=0,f=1;char ch=getchar(); 22 while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();} 23 while(ch>='0'&&ch<='9'){n=n*10+ch-'0';ch=getchar();} 24 return n*f; 25 } 26 27 inline void add(int x,int y,double z) { 28 e[++js].v=y; e[js].cap=z; 29 e[js].nxt=head[x]; head[x]=js; 30 e[++js].v=x; e[js].cap=0; 31 e[js].nxt=head[y]; head[y]=js; 32 } 33 34 inline bool bfs() { 35 for(int i=s;i<=t;i++) dis[i]=-1,vis[i]=0; 36 int h=0,k=1; 37 q[k]=s,dis[s]=0; 38 while(h!=k) { 39 int u=q[++h]; 40 for(int i=head[u];i;i=e[i].nxt) { 41 if(dis[e[i].v]==-1 && e[i].cap) { 42 dis[e[i].v]=dis[u]+1; 43 if(e[i].v==t) return 1; 44 q[++k]=e[i].v; 45 } 46 } 47 } 48 return 0; 49 } 50 51 inline double dfs(int x,double f) { 52 if(x==t) return f; 53 double res=0,t; 54 for(int i=head[x];i;i=e[i].nxt) { 55 if(e[i].cap && dis[e[i].v]==dis[x]+1) { 56 t=dfs(e[i].v,min(e[i].cap,f)); 57 e[i].cap-=t,e[i^1].cap+=t; 58 res+=t,f-=t; 59 if(!f) return res; 60 } 61 } 62 if(!res) dis[x]=-1; 63 return res; 64 } 65 66 inline int dinic() { 67 double res=0; 68 while(bfs()) res+=dfs(s,2e9); 69 return res; 70 } 71 72 inline bool check(double lim) { 73 memset(head,0,sizeof head);js=1; 74 for(int i=1;i<=m;i++) add(d[i].x,d[i].y,min(d[i].z,lim)); 75 return dinic()==ans; 76 } 77 78 int main() { 79 n=read(),m=read(),p=read(); 80 s=1,t=n,R=0; 81 for(int i=1;i<=m;i++) { 82 d[i].x=read(),d[i].y=read(),d[i].z=read(); 83 add(d[i].x,d[i].y,d[i].z); 84 R=max(R,d[i].z); 85 } 86 ans=dinic(); 87 double l=0.0,r=R,mid; 88 while(r-l>1e-6) { 89 mid=(l+r)/2.0; 90 if(check(mid)) r=mid; 91 else l=mid; 92 } 93 printf("%d\n%.5lf\n",ans,1.0*p*mid); 94 return 0; 95 }
