联考20200604 T1 旅游

题目：

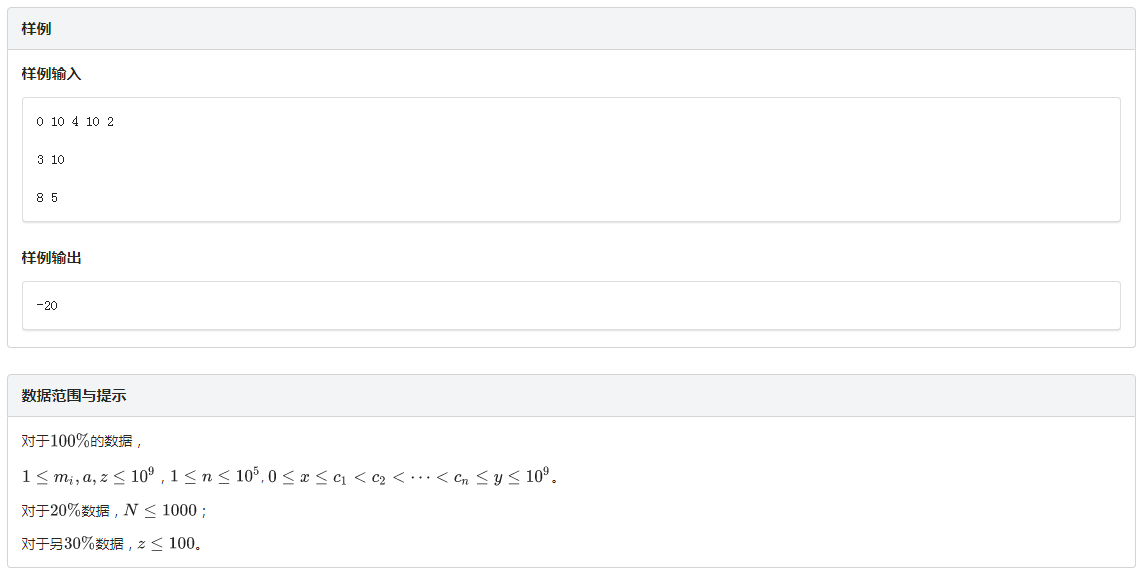
分析：
显然是考虑是否在几个喜爱的城市，中间的城市直接大踏步跨过就好了
列出(DP)式子：
(f[i]=Max_{j=1}^{i-1}f[j]+lceilfrac{c[i]-c[j]}{z} ceil a+m[i])
这个是(O(n^2))的，考虑优化
关键是处理这个式子lceilfrac{c[i]-c[j]}{z} ceil
处理一下得到：
(lceilfrac{c[i]-c[j]}{z} ceil=frac{c[i]}{z}-frac{c[j]}{z}+[j%z<i%z])
([j%z<i%z])把([0,z))分成了([0,c[i]%z))与([c[i]%z,z))，前者有额外1的贡献
于是就以([0,z))为下标，动态开点线段树就好了，单点修改区间求最值

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>

#define maxn 100005

using namespace std;

inline long long getint()
{
	long long num=0,flag=1;char c;
	while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
	while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
	return num*flag;
}

long long x,y,a,z,n;
long long c[maxn],m[maxn],f[maxn];
long long mx[maxn<<5];
int lc[maxn<<5],rc[maxn<<5];
int rt,tot;

inline void insert(int &now,int l,int r,int p,long long num)
{
	if(!now)now=++tot;
	mx[now]=-1ll<<60;
	if(l==r){mx[now]=num;return;}
	int mid=(l+r)>>1;
	if(p<=mid)insert(lc[now],l,mid,p,num);
	else insert(rc[now],mid+1,r,p,num);
	if(lc[now])mx[now]=max(mx[now],mx[lc[now]]);
	if(rc[now])mx[now]=max(mx[now],mx[rc[now]]);
}

inline long long query(int now,int l,int r,int ql,int qr)
{
	if(!now||r<ql||qr<l)return -1ll<<60;
	if(ql<=l&&r<=qr)return mx[now];
	int mid=(l+r)>>1;
	return max(query(lc[now],l,mid,ql,qr),query(rc[now],mid+1,r,ql,qr));
}

int main()
{
	x=getint(),y=getint(),z=getint(),a=getint(),n=getint();
	for(int i=1;i<=n;i++)c[i]=getint(),m[i]=getint();
	if(x<c[1]){for(int i=n;i;i--)c[i+1]=c[i],m[i+1]=m[i];c[1]=x,m[1]=0,n++;}
	if(y>c[n])c[++n]=y;
	f[1]=m[1];
	insert(rt,0,z-1,c[1]%z,f[1]+(c[1]/z)*a);
	for(int i=2;i<=n;i++)
	{
		long long tmp=query(rt,0,z-1,c[i]%z,z-1);
		if(c[i]%z)tmp=max(tmp,query(rt,0,z-1,0,c[i]%z-1)-a);
		f[i]=tmp-(c[i]/z)*a+m[i];
		insert(rt,0,z-1,c[i]%z,f[i]+(c[i])/z*a);
	}
	printf("%lld
",f[n]);
}