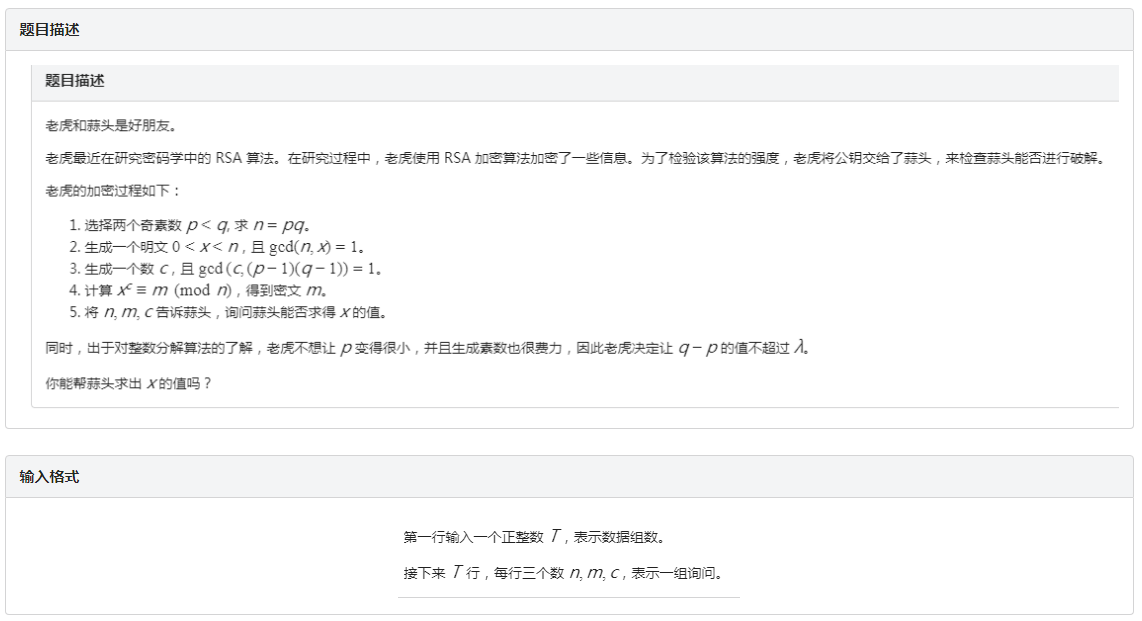
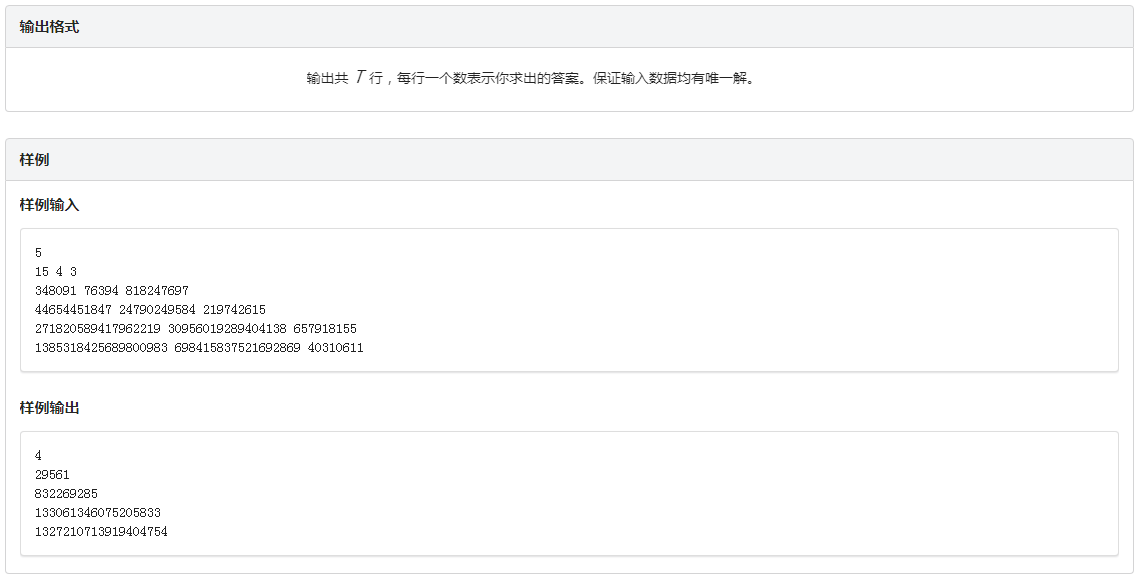
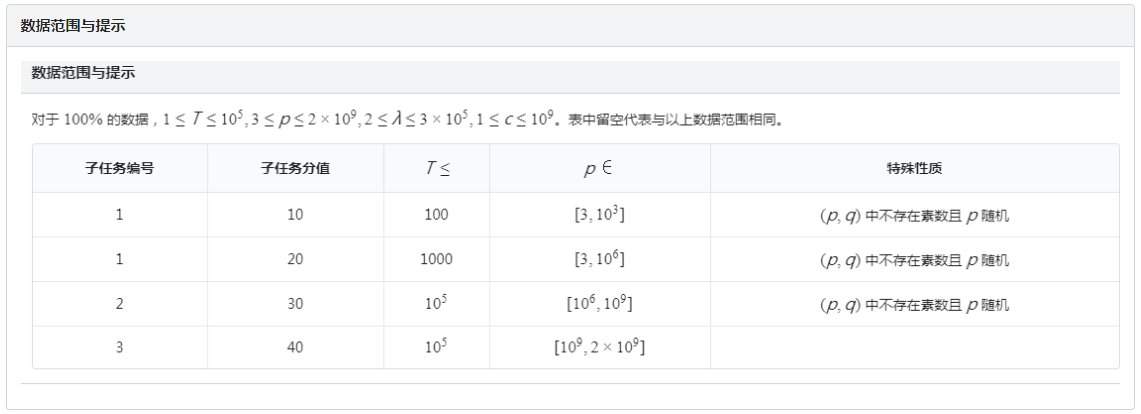
题目:
分析:
考场上暴力都不会写。。。(辣鸡出题人暴力分都没有
发现(n=pq,q-pleq 3e5)这个条件比较有趣,我们从这里入手
设(q-p=y)
(n=p(p+y))
解一元二次方程,舍掉(-Delta)
(p=frac{-y+sqrt{y^2+4n}}{2})
设(t=frac{y}{2})
所以(p=-t+sqrt{t^2+n})
因为(p)是整数,所以(t^2+n=k^2)((k)为整数)
我们分析前三个subtask发现((p,q))中无质数,推测(t)为一个很小的数,于是我们暴力枚举
最后一个subtask由于没有上面的保证,但是(p)在(1e9)级别,那么(sqrt{n})也在(1e9)级别
我们需要(sqrt{k^2-n})为整数,且不大于(3e5)
那么(k^2-n)不大于(9e10)
暴力从(sqrt{n})开始枚举(k),(k)每加一便会使(k^2-n)增加(1e9)级别的量
那么(k)最多每枚举(frac{9e10}{1e9}=90)次
暴力枚举就好了
果然是人类智慧tqlOrz
解出了素数(p,q),我们知道(gcd(c,(p-1)(q-1)=varphi(n))=1),我们解出(d)使得(cdequiv 1(mod varphi(n)))
根据欧拉定理,(xequiv x^{cd}equiv m^d(mod n))
快速幂
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<queue>
#include<iostream>
#include<map>
#include<bitset>
#include<string>
#define maxn 300005
#define INF 1<<30
#define eps 1e-13
using namespace std;
inline long long getint()
{
long long num=0,flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
return num*flag;
}
long long n,m,c,p,q;
long long sq[maxn];
inline long long mul(long long a,long long b,long long p)
{return (a*b-(long long)((long double)a/p*b+eps)*p+p)%p;}
inline long long ksm(long long num,long long k,long long MOD)
{
long long ret=1;
for(;k;k>>=1,num=mul(num,num,MOD))if(k&1)ret=mul(ret,num,MOD);
return ret;
}
inline long long sqr(long long x){return x*x;}
inline void exgcd(long long a,long long b,long long &x,long long &y)
{
if(!b){x=1,y=0;return;}
exgcd(b,a%b,y,x);y-=a/b*x;
}
int main()
{
int T=getint();
for(int i=1;i<=300000;i++)sq[i]=sqr(i);
while(T--)
{
n=getint(),m=getint(),c=getint();
long long k=sqrt(n),t;
for(;(t=sqr(k))-n<=sq[300000];k++)
{
int l=lower_bound(sq,sq+300001,t-n)-sq;
if(sq[l]==t-n){p=k-l,q=k+l;break;}
}
long long x,y,P=(p-1)*(q-1);
exgcd(c,P,x,y);
x=(x%P+P)%P;
printf("%lld
",ksm(m,x,n));
}
}
