题目传送门
分析:
首先考虑树的情况吧
设(f[u][i])表示(u)经过与一些儿子连了边之后剩余(i)的度数
列出式子:
(f[u][i]=f[u][i]*sum[son][1]+f[u][i+1]*sum[son][0])
这里的(sum)是后缀和
设(D)为度数,复杂度为(O(sum D^2))
菊花图直接T到飞起
观察DP式子,发现实际为(D)个2阶多项式全部乘起来,可以使用分治NTT,复杂度变成(O(sum Dlog^{2}D))
然后考虑仙人掌的情况。。。
大佬云:“如何胃疼到没事找事,只需要找一个树上问题,情况改为仙人掌并做出来”
(着实在理
先建出圆方树(注意桥不作为一个单独的方点),但是圆点的dp式子会改变
当儿子为圆点时:
(f[u][i]=f[u][i]*sum[son][1]+f[u][i+1]*sum[son][0])
当儿子为方点时:
(f[u][i]=f[u][i]*sun[son][2]+f[u][i+1]*sum[son][1]+f[u][i+2]*sum[son][0])
方点的情况相当于父亲连着环上的两条边,于是两条边度数变化从{0,1}变成了{0,1,2}
实际还是(D)个低阶多项式乘起来,分治NTT解决
考虑方点的转移。。
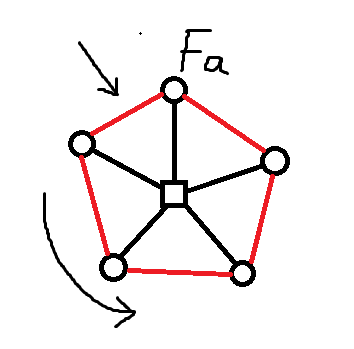
我们取一条原来环上一条连接方点儿子和父亲的边,强行确定它的方向
然后按顺序进行dp
(实际上这个dp就是乘法,满足交换律,不需要沿着环边顺序)
设(g[0/1][u][0/1])表示确定第一条边朝向(0/1)后(u)是否被上一个点指向,(u)为表示环的方点
初始时(g[0][u][0]=1,g[1][u][1]=1)
(g[u][0]=g[u][0]*f[son][1]+g[u][1]*f[son][2])
(g[u][1]=g[u][0]*f[son][0]+g[u][1]*f[son][1])
(f[fa][2]=g[1][u][0],f[fa][1]=g[1][u][1]+g[0][u][0],f[fa][0]=g[0][u][1])
暴力转移,复杂度是线性的
然后OJ很卡,疯狂卡常。。。。
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<iostream>
#include<map>
#include<string>
#define maxn 200005
#define MOD 998244353
#define Poly vector<int>
using namespace std;
inline int getint()
{
int num=0,flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
return num*flag;
}
int n,m,tot;
int f[maxn][3],vis[maxn],a[maxn];
vector<int>V[maxn],id[maxn];
Poly p[maxn];
int d[maxn];
int fir[maxn],nxt[maxn],to[maxn],cnt;
int Wl,Wl2,w[maxn<<2];
int rev[maxn<<2];
int dfn[maxn],low[maxn],tim,stk[maxn],tp;
int ksm(int num,int k)
{
int ret=1;
for(;k;k>>=1,num=1ll*num*num%MOD)if(k&1)ret=1ll*ret*num%MOD;
return ret;
}
void init(int N)
{
Wl=w[0]=1;
while((Wl<<1)<=N)Wl<<=1;
w[1]=ksm(3,(MOD-1)/(Wl<<1)),Wl2=Wl<<1;
for(int i=2;i<=Wl2;i++)w[i]=1ll*w[i-1]*w[1]%MOD;
}
int upd(int x){return x<MOD?x:x-MOD;}
void newnode(int u,int v)
{to[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt;}
void tarjan(int u)
{
dfn[u]=low[u]=++tim;stk[++tp]=u;
for(int i=0;i<V[u].size();i++)if(!vis[id[u][i]])
{
int v=V[u][i];vis[id[u][i]]=1;
if(!dfn[v])
{
tarjan(v),low[u]=min(low[u],low[v]);
if(low[v]==dfn[u])
{
newnode(u,++tot);int x;
do{x=stk[tp--],newnode(tot,x);}while(x!=v);
}
else if(low[v]>dfn[u])newnode(u,v),tp--;
}
else low[u]=min(low[u],dfn[v]);
}
}
void NTT(Poly &a,int opt,int N)
{
for(int i=0;i<N;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
for(int i=1,B=Wl;i<N;i<<=1,B>>=1)
for(int j=0,t=i<<1;j<N;j+=t)for(int k=0,x=0;k<i;k++,x+=B)
{
int v=1ll*a[i+j+k]*w[opt==1?x:Wl2-x]%MOD;
a[i+j+k]=upd(a[j+k]-v+MOD),a[j+k]=upd(a[j+k]+v);
}
if(!~opt)for(int i=0,Inv=ksm(N,MOD-2);i<N;i++)a[i]=1ll*a[i]*Inv%MOD;
}
Poly mul(Poly A,Poly B)
{
int len=A.size()+B.size()-1,N=1;
while(N<len)N<<=1;A.resize(N),B.resize(N);
for(int i=0;i<N;i++)rev[i]=(rev[i>>1]>>1)|(i&1?N>>1:0);
NTT(A,1,N),NTT(B,1,N);
for(int i=0;i<N;i++)A[i]=1ll*A[i]*B[i]%MOD;
NTT(A,-1,N);A.resize(len);
return A;
}
Poly solve(int l,int r)
{
if(l==r)return p[l];
int mid=(l+r)>>1;
return mul(solve(l,mid),solve(mid+1,r));
}
void dfs(int u)
{
for(int i=fir[u];i;i=nxt[i])dfs(to[i]);
if(u<=n)
{
if(!fir[u]){f[u][0]=1,f[u][1]=(a[u]>=1),f[u][2]=(a[u]>=2);return;}
cnt=0;
for(int i=fir[u];i;i=nxt[i])
{
p[++cnt].clear();
if(to[i]>n)p[cnt].push_back(f[to[i]][2]);
p[cnt].push_back(f[to[i]][1]),p[cnt].push_back(f[to[i]][0]);
}
Poly A=solve(1,cnt);A.resize(a[u]+1);
for(int i=1;i<=a[u];i++)A[i]=upd(A[i]+A[i-1]);
f[u][0]=A[a[u]];
if(a[u]>=1)f[u][1]=A[a[u]-1];
if(a[u]>=2)f[u][2]=A[a[u]-2];
}
else
{
for(int k=0;k<=1;k++)
{
int g0=!k,g1=k;
for(int i=fir[u];i;i=nxt[i])
{
int tmp0=upd((1ll*g0*f[to[i]][1]+1ll*g1*f[to[i]][2])%MOD);
int tmp1=upd((1ll*g0*f[to[i]][0]+1ll*g1*f[to[i]][1])%MOD);
g0=tmp0,g1=tmp1;
}
f[u][k+1]=upd(f[u][k+1]+g0),f[u][k]=upd(f[u][k]+g1);
}
}
}
int main()
{
n=getint(),m=getint();
init(2*n);
for(int i=1;i<=m;i++)
{
int u=getint(),v=getint();
V[u].push_back(v),V[v].push_back(u);d[u]++,d[v]++;
id[u].push_back(i),id[v].push_back(i);
}
for(int i=1;i<=n;i++)a[i]=min(getint(),d[i]);
tot=n,tarjan(1),dfs(1);
printf("%d
",f[1][0]);
}
