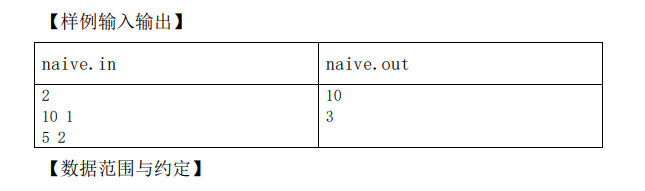
题目


分析:
乍一看不就是从楼上扔鸡蛋那道题吗。。。
然后开始写写写。。。
设f [ i ] [ j ]表示 i 个记者膜 j 次可以验证多少层楼。。。
于是开始递推:
我们选取第 i 个记者去尝试其中一层楼y
如果他被续了(续和膜蛤是sm意思啊2333)

/*龙门粗口*/
如果他被续了,那么说明x<y,然后研究子问题f [ i-1 ] [ j-1 ]
如果他没被续,那么说明x>=y,然后研究子问题f [ i ] [ j-1 ]
包括自己所在这层楼,所以递推式为:
f [ i ] [ j ] = f [ i ] [ j-1 ] + f [ i-1 ] [ j-1 ] + 1
于是我们可以预处理出答案,然后询问时lowerbound就好了。。。
我记得当时开的f[64][64]来着。。。
开了,美滋滋。。。。
一个小时后。。。
不对!!!!
这样连n=100,k=1都算不对?!
突然想起原题有这样一个限制,如果尝试次数超过64就直接输出-1!
差点翻车。。。
于是就往大了开
开到了f[64][100000]
这样能算多少呢。。。
嗯,当k>3时,都是算的出来的。。。
那么找一下k=1,2,3的规律吧。。
k=1时,ans就是n
k=2时,ans满足ans*(ans+1)/2>=n
k=3时。。。
不会诶。。。
那么为3新开一个怎么样
又开了个g[3][3000000]
咦,跑出来了,稳了。。。
结果。。。
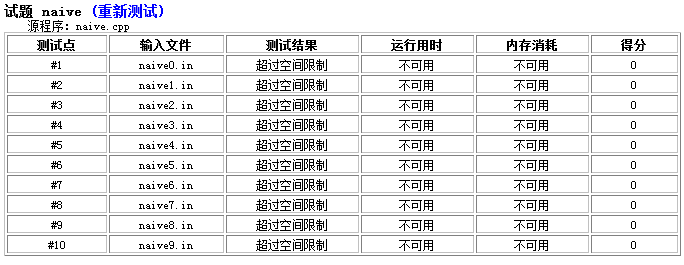
枯了出来。。。
真该死啊,改小一点就过了。。。
但是这道题的奇奇怪怪的技巧有必要记一下2333

#include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #include<vector> #define maxn 100005 #define maxm 65 #define INF 1000000000000000000ll using namespace std; inline long long getint() { long long num=0,flag=1;char c; while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1; while(c>='0'&&c<='9')num=num*10+c-48,c=getchar(); return num*flag; } long long f[maxm][maxn]; long long g[4][20*maxn]; long long N,K; inline void init() { for(int i=1;i<maxm;i++)for(int j=1;j<maxn;j++)f[i][j]=min(f[i][j-1]+f[i-1][j-1]+1,INF); for(int i=1;i<=3;i++)for(int j=1;j<20*maxn;j++)g[i][j]=min(g[i][j-1]+g[i-1][j-1]+1,INF); } inline void solve(long long N) { long long l=1,r=1ll<<31; while(l<r) { long long mid=(l+r)>>1; if(1ll*mid*(mid+1)/2<N)l=mid+1; else r=mid; } printf("%lld ",l); } int main() { int T=getint(); init(); while(T--) { N=getint(),K=getint(); if(K==1)printf("%lld ",N); else if(K==2)solve(N); else if(K==3)printf("%d ",lower_bound(g[K]+1,g[K]+20*maxn,N)-g[K]); else printf("%d ",lower_bound(f[K]+1,f[K]+maxn,N)-f[K]); } }

