Description
操场可以看成一个平面直角坐标系,在操场上有n*n个同学。你希望将这n*n个同学排成一个间距为1的n*n的方阵,并且要求方阵的左边界在y轴上。每个同学在初始格点(xi,yi)上,可以移动到任何一个格点(xi’,yi’),耗费的体力值为(|xi-xi’|+|yi-yi’|)^p,xi,yi是整数,p是正整数。现在你想知道,将这n*n同学移动成符合要求的方阵的情况下,总共耗费的体力值最小是多少。
Input
每个测试点包含多组测试数据,第一行一个正整数t,表示有t组测试数据。接下来有t个部分。每个部分第一行两个正整数n,p,含义如上所述,接下来n*n行,每行两个整数,表示每个同学的坐标。
Output
输出t行,每行一个整数,表示这一组测试数据的总共耗费最小体力值。
Sample Input
2 2 1 0 2 2 1 3 1 3 2 2 2 0 0 0 1 1 0 2 2
Sample Output
6 4 【样例说明】 Case #1: (2,1) -> (0,1) cost 2 (3,1) -> (1,1) cost 2 (3,2) -> (1,2) cost 2 Case #2: (2,2) - > (1,1) cost 4
Data Constraint
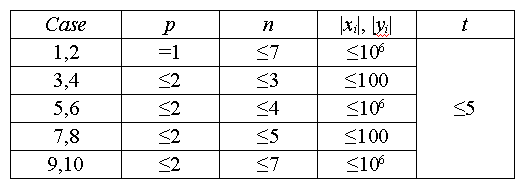
真好呢,突然换题搞得只有三个小时考
刚看时一脸懵逼
只会3,4,7,8的40分
暴力枚举方阵位置,跑费用流
接下来思考特性
感性(dabiao)发现当方阵位置变化,其最优值,是一个单峰函数(联想绝对值方程)
单峰函数可以三分
于是这就是一道三分费用流模板题。。。