题目背景
墙上贴着许多形状相同的海报、照片。它们的边都是水平和垂直的。每个矩形图片可能部分或全部的覆盖了其他图片。所有矩形合并后的边长称为周长。
题目描述
编写一个程序计算周长。
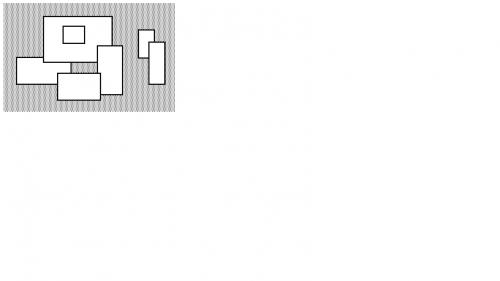
如图1所示7个矩形。
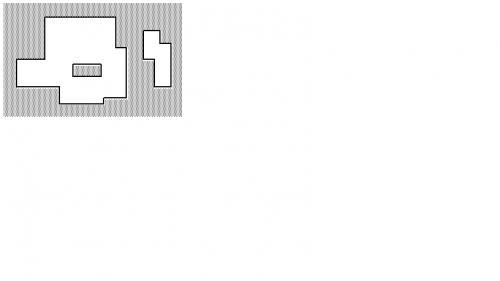
如图2所示,所有矩形的边界。所有矩形顶点的坐标都是整数。
解析
首先想到模拟,这题数据小,直接暴力扫转折点,统计周长的增量就得了。
其实最优解就是这么做的。
TAG里有扫描线,咱就用扫描线吧。
简单来说,还是扫描线同样的思路,做线段覆盖(具体实现可以百度,我懒得写了)。入边权值为+1,出边权值为-1,从下到上扫一遍,从左到右扫一遍,在遇到入边时,统计当前扫描线与上一条之间覆盖线段长度的增量,这个增量具体来说就是做差。
简单的正确性证明:对于上述每一个增量,其都是由入边造成的,那么这个增量最终都会被出边抵消。因此若我们只统计入边造成的增量,其两倍就是总矩形周长。其实非常好想。
参考代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<vector>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 20010
#define MOD 2520
#define E 1e-12
using namespace std;
inline int read()
{
int f=1,x=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
struct node{
int l,r,h,v;
bool operator<(const node &a)const{
if(a.h==h) return a.v<v;
return a.h>h;
}
}h[N],l[N];
struct tree{
int l,r;
int cnt,dat;
}t[N<<2];
int n,hh[N],hl[N],cmd;
inline void pushup(int p)//线段覆盖
{
if(t[p].cnt){
if(cmd==1) t[p].dat=hh[t[p].r+1]-hh[t[p].l];
else t[p].dat=hl[t[p].r+1]-hl[t[p].l];
}
else if(t[p].l==t[p].r) t[p].dat=0;
else t[p].dat=t[p<<1].dat+t[p<<1|1].dat;
}
inline void build(int p,int l,int r)
{
t[p].l=l,t[p].r=r;
t[p].cnt=t[p].dat=0;
if(l==r) return;
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
}
inline void change(int p,int l,int r,int val)
{
if(l<=t[p].l&&t[p].r<=r){
t[p].cnt+=val;
pushup(p);
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(l<=mid) change(p<<1,l,r,val);
if(r>mid) change(p<<1|1,l,r,val);
pushup(p);
}
int main()
{
n=read();
int cnth=0,cntl=0,th=0,tl=0;
for(int i=1;i<=n;++i){
int x1,x2,y1,y2;
x1=read(),y1=read(),x2=read(),y2=read();
h[++cnth].l=x1,h[cnth].r=x2,h[cnth].h=y1,h[cnth].v=1;
l[++cntl].l=y1,l[cntl].r=y2,l[cntl].h=x1,l[cntl].v=1;
h[++cnth].l=x1,h[cnth].r=x2,h[cnth].h=y2,h[cnth].v=-1;
l[++cntl].l=y1,l[cntl].r=y2,l[cntl].h=x2,l[cntl].v=-1;
hh[++th]=x1,hh[++th]=x2;
hl[++tl]=y1,hl[++tl]=y2;
}
sort(hh+1,hh+th+1);sort(hl+1,hl+tl+1);
sort(h+1,h+cnth+1);sort(l+1,l+cntl+1);
unique(hh+1,hh+th+1);unique(hl+1,hl+tl+1);
int ans=0,tmp=0;
build(1,1,cnth);
cmd=1;
for(int i=1;i<=cnth;++i){
int x,y;
x=lower_bound(hh+1,hh+th+1,h[i].l)-hh;
y=lower_bound(hh+1,hh+th+1,h[i].r)-hh-1;
change(1,x,y,h[i].v);
if(h[i].v==1)ans+=t[1].dat-tmp;
tmp=t[1].dat;
}
build(1,1,cntl);
cmd=2,tmp=0;
for(int i=1;i<=cntl;++i){
int x,y;
x=lower_bound(hl+1,hl+tl+1,l[i].l)-hl;
y=lower_bound(hl+1,hl+tl+1,l[i].r)-hl-1;
change(1,x,y,l[i].v);
if(l[i].v==1)ans+=t[1].dat-tmp;
tmp=t[1].dat;
}
ans<<=1;
cout<<ans<<endl;
return 0;
}