题目描述
每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶
牛都是自恋狂,每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果A喜
欢B,B喜欢C,那么A也喜欢C。牛栏里共有N 头奶牛,给定一些奶牛之间的爱慕关系,请你
算出有多少头奶牛可以当明星。
解析
又是一道水题emmm。
容易发现,缩点之后的图中,能当明星的最多只有一个点,超过一个就不合法。
如下图中的红色点中所有奶牛都可以当明星。
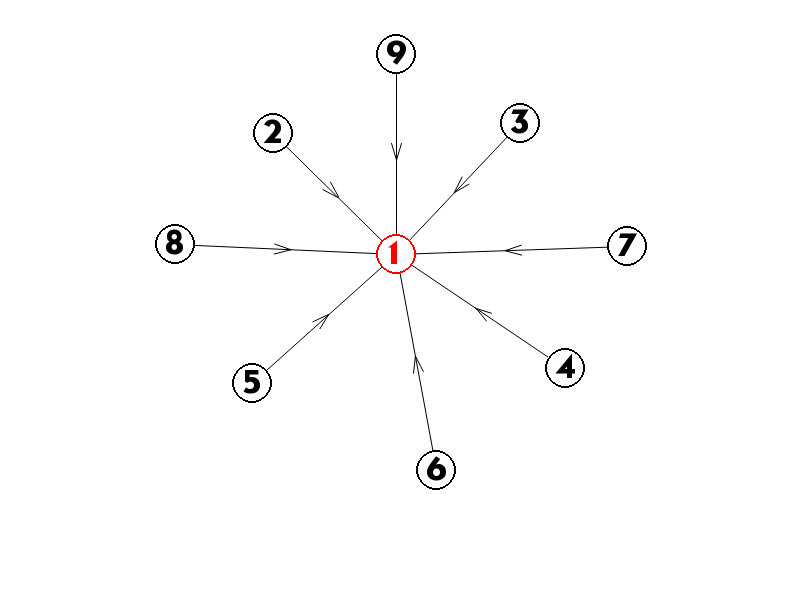
而下面这种情况,因为紫色节点的存在,显然不合法。
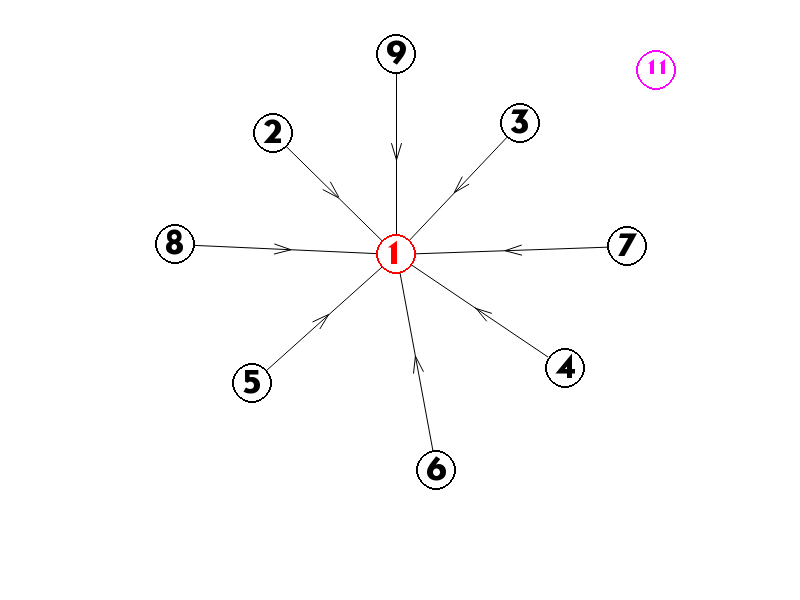
如果缩点后的图是一棵树,也是显然不合法的。
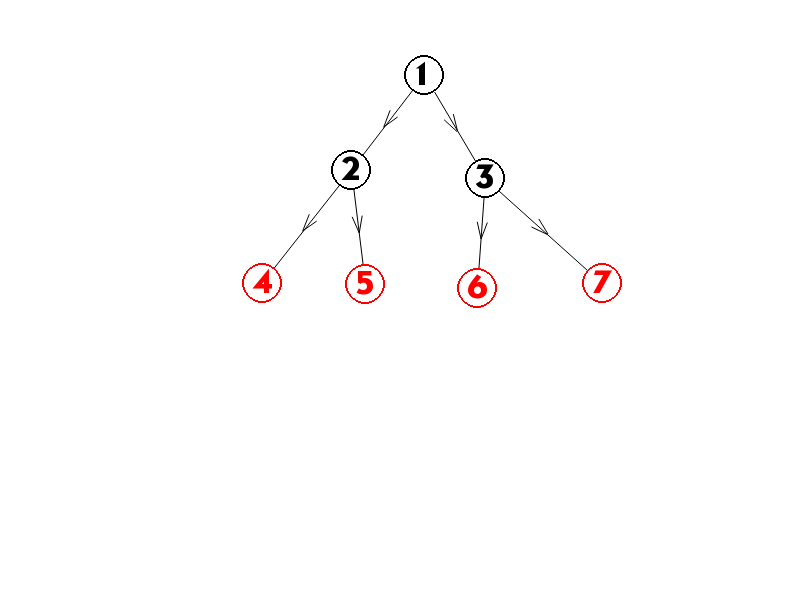
于是我们在缩点之后的图上统计一下出度为0的节点的数量就好了。
参考代码
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#define N 50010
using namespace std;
inline int read()
{
int f=1,x=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
struct rec{
int next,ver;
}g[N],G[N];
int head[N],headG[N],tot,totG,n,m,low[N],dfn[N];
int stack[N],top,c[N],cnt,otg[N],idt,scc[N];
bool ins[N],v[N];
inline void add(int x,int y)
{
g[++tot].ver=y;
g[tot].next=head[x],head[x]=tot;
}
inline void addG(int x,int y)
{
G[++totG].ver=y;
G[totG].next=headG[x],headG[x]=totG;
otg[x]++;
}
inline void tarjan(int x)
{
dfn[x]=low[x]=++cnt;
stack[++top]=x,ins[x]=1;
for(int i=head[x];i;i=g[i].next){
int y=g[i].ver;
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
}
else if(ins[y]) low[x]=min(low[x],dfn[y]);
}
if(low[x]==dfn[x]){
int y;idt++;
do{
y=stack[top--],ins[y]=0;
c[y]=idt;scc[idt]++;
}while(x!=y);
}
}
int main()
{
n=read(),m=read();
for(int i=1;i<=m;++i){
int u,v;
u=read(),v=read();
add(u,v);
}
for(int i=1;i<=n;++i)
if(!dfn[i]) tarjan(i);
for(int x=1;x<=n;++x)
for(int i=head[x];i;i=g[i].next){
int y=g[i].ver;
if(c[x]==c[y]) continue;
addG(c[x],c[y]);
}
int ans=0,tmp=0;
for(int i=1;i<=idt;++i)
if(otg[i]==0){
ans+=scc[i],tmp++;
if(tmp>1){
printf("0
");
return 0;
}
}
cout<<ans<<endl;
return 0;
}