题目来源:洛谷
题目描述
多米诺骨牌有上下2个方块组成,每个方块中有1~6个点。现有排成行的
上方块中点数之和记为S1,下方块中点数之和记为S2,它们的差为|S1-S2|。例如在图8-1中,S1=6+1+1+1=9,S2=1+5+3+2=11,|S1-S2|=2。每个多米诺骨牌可以旋转180°,使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。
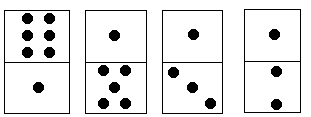
对于图中的例子,只要将最后一个多米诺骨牌旋转180°,可使上下2行点数之差为0。
输入输出格式
输入格式:
输入文件的第一行是一个正整数n(1≤n≤1000),表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数,表示多米诺骨牌上下方块中的点数a和b,且1≤a,b≤6。
输出格式:
输出文件仅一行,包含一个整数。表示求得的最小旋转次数。
输入输出样例
解析:
灰常好的一道高质量题目。通过这道题,可以让你稍稍理解到背包问题的本质。【可行性背包】
看到其他地方上没什么人讲,实际上这也是一个衍生出来的背包问题,模板题参见 poj1742。
具体什么是可行性背包,按照我个人理解,实质上就是在每一个新物品加入背包时,更新之前的状态能转移到当前状态的状态,其他状态不转移。
我们知道,背包问题一般有一个背包容量W,一些物品体积V1~Vn,以及这些物品对应的价值C1~Cn。
对于可行性背包,实际上我们是对整个背包容量W进行了一次遍历,寻找可以放置下一个物品的位置,然而由于这些物品的某些性质,使得对于容积为W的背包的某个容量wi,所有放置物品的方案都无法使容积到达wi。
比如我们有体积为2,5,6,10的四个物品和一个容积为20的背包,那么显然这个背包不可能只装体积为1的物品。
也就是说,对于每一个要放进背包的物品,我们都要检查一遍从各个状态能否转移到当前状态。
这就是背包的本质:每一个物品或动作对所有当前状态的更新。对于不可行的解,我们排除之,对于可行解,我们求之。
对于这道题,确实比较难看出可行性背包,而且状态设计也是个难点,更别说那个该死的绝对值。。。
我们一一解决它们。
首先对于这个绝对值,我们可以发现一个规律:对于一组数据,无论怎么反转牌,它们的点数总和相等。
很容易就想到对于任意的1~i个牌,点数总和减去上面的1~i个牌的点数和就是下面对应的1~i个牌的点数和。
绝对值可解,我们只要想办法把其中一行的最优解求出来,下面那一行就是可导的。
状态设计是最苟的。如果你之前没做过可行性背包,那就会像我一样想一个晚上也想不出来正解,倒是贪心啊暴力啥的解法往脑子里蹦。
为什么我们那可行性背包来做?首先是这个题满足一个背包的本质要求,就是使某个属性最优时,另一个属性的最优情况,在这道题里面最优就是上下差值最小时的最小转动次数。然后就是因为我们有很多不同的装入背包方案,然而我们并不知道:1、哪一种是最优 2、哪一种可以通过翻转转出来。而且这明显是需要一个约束,即上下差值最小时的最小转动次数。
我们假设dp[i][j]表示转动第i个牌时,上面那一行总和为j时的最小转动次数(这是可行性背包的模板,好好理解这个j),对于每次“加入"背包的牌,我们有翻转和不翻转两种决策,没转就继承上一个状态,转了就把次数加一。
状态转移方程:
if(j>=a[i]) dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]]);//不转
if(j>=b[i]) dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1);//转动
初始状态:
假设上面那一排的输入数据为up[],下面那一行为down[];
如果第一个牌上下不等,那么就是dp[1][up[1]]=0,dp[1][down[1]]=1,也就是最开始可以把下面的牌转动到上面;
如果第一个牌上下相等,就是dp[1][up[1]]=dp[1][down[1]]=0,就是转不转都一样嘛。
很好,由于是可行性背包,现在我们只需要注意一下背包容量也就是状态大小到达了6*n,就是最大总和。
完事。
参考代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<string> 7 #include<cstdlib> 8 #include<queue> 9 #include<vector> 10 #define INF 0x3f3f3f3f 11 #define PI acos(-1.0) 12 #define N 1010 13 #define MOD 2520 14 #define E 1e-12 15 using namespace std; 16 int dp[N][N*6],a[N],b[N],cnt; 17 int main() 18 { 19 int n; 20 cin>>n; 21 for(int i=1;i<=n;i++) 22 scanf("%d%d",&a[i],&b[i]),cnt+=a[i]+b[i]; 23 memset(dp,0x3f,sizeof(dp)); 24 if(a[1]!=b[1]) dp[1][a[1]]=0,dp[1][b[1]]=1; 25 else dp[1][a[1]]=0,dp[1][b[1]]=0; 26 //对于任意一个牌i,到i的可能的和可以达到6*n 27 //状态设计为dp[i][j]表示到第i个牌,若上面那一行的总和为j时所能得到的最少转动次数 28 for(int i=2;i<=n;i++) 29 for(int j=0;j<=6*n;j++){ 30 if(j>=a[i]) dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]]);//不转 31 if(j>=b[i]) dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1);//转动 32 } 33 34 int minc=INF,ans=INF;//minc最小差值,ans最小交换次数 35 for(int i=0;i<=cnt;i++){ 36 if(dp[n][i]<INF){//如果总和为i的情况存在 37 if(abs(i-(cnt-i))<minc){//记下最小差值和最小交换次数 38 minc=abs(i-(cnt-i));ans=dp[n][i]; 39 } 40 else if(abs(i-(cnt-i))==minc)//在最小差值最小时,还要比较交换次数 41 ans=min(ans,dp[n][i]); 42 } 43 } 44 cout<<ans<<endl; 45 return 0; 46 }