3757: 苹果树
Time Limit: 20 Sec Memory Limit: 256 MBSubmit: 1305 Solved: 503
[Submit][Status][Discuss]
Description
神犇家门口种了一棵苹果树。苹果树作为一棵树,当然是呈树状结构,每根树枝连接两个苹果,每个苹果都可以沿着一条由树枝构成的路径连到树根,而且这样的路径只存在一条。由于这棵苹果树是神犇种的,所以苹果都发生了变异,变成了各种各样的颜色。我们用一个到n之间的正整数来表示一种颜色。树上一共有n个果。苹每个苹果都被编了号码,号码为一个1到n之间的正整数。我们用0代表树根。只会有一个苹果直接根。
有许许多多的人来神犇家里膜拜神犇。可神犇可不是随便就能膜拜的。前来膜拜神犇的人需要正确回答一个问题,才能进屋膜拜神犇。这个问题就是,从树上编号为u的苹果出发,由树枝走到编号为v的苹果,路径上经过的苹果一共有多少种不同的颜色(包括苹果u和苹果v的颜色)?不过神犇注意到,有些来膜拜的人患有色盲症。具体地说,一个人可能会认为颜色a就是颜色b,那么他们在数苹果的颜色时,如果既出现了颜色a的苹果,又出现了颜色b的苹果,这个人只会算入颜色b,而不会把颜色a算进来。
神犇是一个好人,他不会强人所难,也就会接受由于色盲症导致的答案错误(当然答案在色盲环境下也必须是正确的)。不过这样神犇也就要更改他原先数颜色的程序了。虽然这对于神犇来说是小菜一碟,但是他想考验一下你。你能替神犇完成这项任务吗?
Input
Output
输出一共m行,每行仅包含一个整数,代表这个人应该数出的颜色种数。
Sample Input
1 1 3 3 2
0 1
1 2
1 3
2 4
3 5
1 4 0 0
1 4 1 3
1 4 1 2
Sample Output
1
2
HINT
Source
Solution
树上莫队裸题,下面来说说树上莫队
序列上的莫队没什么好说的,至于树上莫队,思想是一样的
对树DFS分块(详见 BZOJ-1086王室联邦哦),然后对询问排序,然后处理就好,那么就是具体的实现了
至于树分块,就是按照DFS时间戳去搞,所以询问排序的第一关键字就是所在的块,第二关键字就是时间戳
至于如何把树上的一条路径,转化为一端区间?
首先我们设$S(u,v)$表示$u-v$的路径上的点集,$LCA(u,v)$表示两点的最近公共祖先,$root$为树根
$xor$为集合的对称差,即 只属于其中一个集合,而不属于另一个集合的元素组成的集合
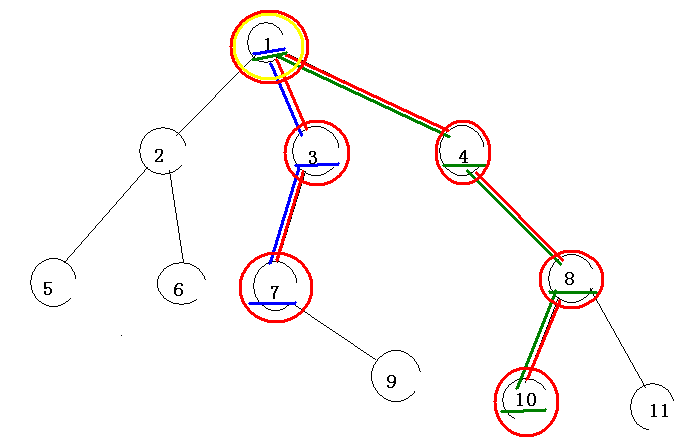
那么发现$S(u,v)=S(root,u) xor S(root,v) xor LCA(u,v)$ (不懂见下图哦)
就是节点出现两次消掉
再有$T(u,v)=S(root, v) xor S(root, u)$
观察将询问$curV$移动到$targetV$前后$T(curV, curU)$变化:
$T(curV, curU)=S(root, curV) xor S(root, curU)$
$T(targetV, curU)=S(root, targetV) xor S(root, curU)$
取对称差:
$T(curV, curU) xor T(targetV, curU)= (S(root, curV) xor S(root, curU)) xor (S(root, targetV) xor S(root, curU))$
由于对称差的交换律、结合律:
$T(curV, curU) xor T(targetV, curU)= S(root, curV) xorS(root, targetV)$
两边同时$xor T(curV, curU)$:
$T(targetV, curU)= T(curV, curU) xor S(root, curV) xor S(root, targetV)$
$T(targetV, curU)=T(curV, curU) xor T(curV, targetV)$
也就是说,更新的时候,$xor T(curV, targetV)$就行了。
Code
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> using namespace std; int read() { int x=0;char ch=getchar(); while(ch<'0'||ch>'9') ch=getchar(); while(ch>='0'&&ch<='9') {x=x*10+ch-'0';ch=getchar();} return x; } #define maxn 50100 #define maxq 100100 int n,m,fk,knum,ans,root; struct Edgenode{int to,next;}edge[maxn<<1]; int head[maxn],cnt=1; void add(int u,int v) {cnt++;edge[cnt].next=head[u];head[u]=cnt;edge[cnt].to=v;} void insert(int u,int v) {add(u,v); add(v,u);} int deep[maxn],father[maxn][25],dfsx,stack[maxn],top,rt[maxn],an[maxq],p[maxn]; struct Pointnode{int dfs,col;}po[maxn]; struct Asknode { int a,b,u,v,id; bool operator < (const Asknode & A) const { if(rt[u]==rt[A.u]) return po[v].dfs<po[A.v].dfs; else return rt[u]<rt[A.u]; } }q[maxq]; bool visit[maxn]; int DFS(int now) { int size=0; po[now].dfs=++dfsx; for (int i=1; i<=20; i++) if (deep[now]>=(1<<i)) father[now][i]=father[father[now][i-1]][i-1]; for (int i=head[now]; i; i=edge[i].next) if (edge[i].to!=father[now][0]) { deep[edge[i].to]=deep[now]+1; father[edge[i].to][0]=now; size+=DFS(edge[i].to); if (size>=fk) { knum++; for(int j=1; j<=size; j++) rt[stack[top--]]=knum; size=0; } } stack[++top]=now; return size+1; } int LCA(int x,int y) { if (deep[x]<deep[y]) swap(x,y); int dd=deep[x]-deep[y]; for (int i=0; i<=20; i++) if (dd&(1<<i) && dd>=(1<<i)) x=father[x][i]; for (int i=20; i>=0; i--) if (father[x][i]!=father[y][i]) x=father[x][i],y=father[y][i]; if (x==y) return x; else return father[x][0]; } void reserv(int x) { if (!visit[x]) {visit[x]=1; p[po[x].col]++; if (p[po[x].col]==1) ans++;} else {visit[x]=0; p[po[x].col]--; if (p[po[x].col]==0) ans--;} } void work(int u,int v) { while (u!=v) if (deep[u]>deep[v]) reserv(u),u=father[u][0]; else reserv(v),v=father[v][0]; } int main() { n=read(),m=read(); fk=sqrt(n); for (int i=1; i<=n; i++) po[i].col=read(); for (int u,v,i=1; i<=n; i++) { u=read(),v=read(); if (!u) root=v; else if (!v) root=u; else insert(u,v); } DFS(root); knum++; while (top) rt[stack[top--]]=knum; for (int i=1; i<=m; i++) { q[i].u=read();q[i].v=read();q[i].a=read();q[i].b=read();q[i].id=i; if (po[q[i].u].dfs>po[q[i].v].dfs) swap(q[i].u,q[i].v); } sort(q+1,q+m+1); int T=LCA(q[1].u,q[1].v); work(q[1].u,q[1].v); reserv(T); an[q[1].id]=ans; if (p[q[1].a] && p[q[1].b] && q[1].a!=q[1].b) an[q[1].id]--; reserv(T); for (int i=2; i<=m; i++) { work(q[i-1].u,q[i].u); work(q[i-1].v,q[i].v); T=LCA(q[i].u,q[i].v); reserv(T); an[q[i].id]=ans; if(p[q[i].a] && p[q[i].b] && q[i].a!=q[i].b) an[q[i].id]--; reserv(T); } for (int i=1; i<=m; i++) printf("%d ",an[i]); return 0; }