先是一些定义类的东西
1.len表示字符串串长
2.S[i~j]表示字符串中第i个字符到第i+j个字符所组成的串
3.后缀Suffix(i) 表示从i开始到len的子串,所以显然有Suffix(i)=S[i~len]
4.关于字符串之间的比较,一般采用字典序来比较:
也就是说设两个串S1,S2进行比较;
指针为i,如果S1[i]==S2[i]那么i++
如果S1[i]<S2[i],则S1<S2,反之同理
如果len(S1)<i,则S1<S2,反之同理
基于后缀的定义,很显然,在比较的过程中,绝对不会出现相同的两个串
5.后缀数组SA[]:Suffix(SA[i])<Suffix(SA[i+1]),1≤i<n。也就是将S的n个后缀从小到大进行排序之后把排好序的后缀的开头位置顺次放入SA中。
或者说,SA[i]存放的是排名为i的那个后缀的开头字符在字符串中的位置,即SA[i]为排名为i的后缀是从原串第几个位置开始的
6.名次数组rank[]:存放Suffix(i)在所有后缀中的排名
发现rank[]和SA[]其实是互逆的,所以求得其中一个,即可以得到另一个
7.height数组: 定义height[i]=Suffix(SA[i-1])和Suffix(SA[i])的LCP(最长公共前缀)
有一个技巧,为了方便的比较大小,可以在字符串后面先添加一个字符,但这个字符必须未出现过,且小于之前的所有字符.这样在求出rank数组以后,可以O(1)的比较任意两个后缀的大小,根据比较的模式,两后缀比较,最多需要比较n次;
下面是具体实现的方法:分为两种方法 倍增(DA)算法 以及 DC3算法
倍增算法的复杂度是O(nlogn)的,DC3的复杂度是O(n)的,但倍增的常数应该会小一些,而且更容易实现和理解,故学习的DA
思路就是倍增;
对每个字符开始的长度为$2^{k}$的子串进行排序,求出rank.k从零开始每次+1
很显然的就是rank中是不可能有重复的存在,一定唯一.比较好的方法,每次排序都利用上一次的子串,即长度为$2^{k-1}$的rank值,那么这个长度为$2_{k}$的字符串就可以用两个长度为$2^{k-1}$的子串来作为关键字来表示,然后可以进行排序,至于一个比较稳定且效率较优的排序,通常使用O(n)的基数排序(不是很懂网上说的"计"数TAT)
至于基数排序,大体上就是类似于分层次的桶排?
把待排序的东西分成一些"层次",那么每次按当前层进行排序,按顺序扔进桶中,最后在按桶的顺序出桶,所有层都这么处理完后的顺序即为顺序,比较好理解的就是对于数的排序,即可以理解为把每个数位看成每个层来考虑.这里是用表示每个串的两个短串去当关键字
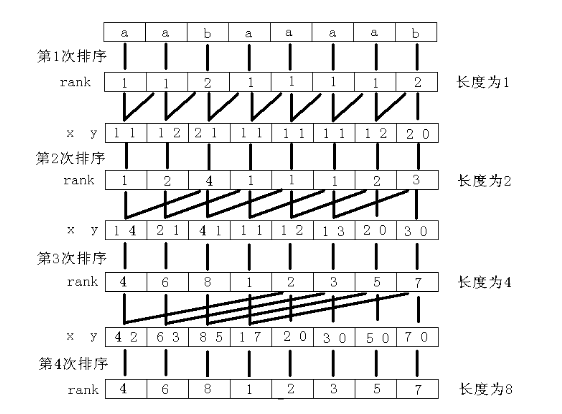
第一步:对于H=1的字符串排序
第二步:若干次基数排序,有个优化,第一次要对第二关键字排序,第二次是对第一关键字排序;而对于第二关键字的排序结果,可以利用上一次求得的SA直接算出,那么没必要再做一次
第三步:求出新的SA后,需要求解rank;这里的时候,rank可能会重复,这时候就需要比较是否完全相同了;还有一个小技巧:就是开个别数组的时候,可以开成指针类型,这样就可以直接实现整个数组的复制
这样之后,基本就完成了.至于时间复杂度,每次基数排序的复杂度是O(n)的,而排序次数取决于最长公共子串,最坏是logn级别,所以时间复杂度是O(nlogn)
至于一些应用:
最长公共前缀LCP,这里引出height数组
那么height数组有一些性质:
对于j,k,设rank[j]<rank[k],那么
Suffix(j)和Suffix(k)的LCP为min(height[rank[j]+1]~height[rank[k]])
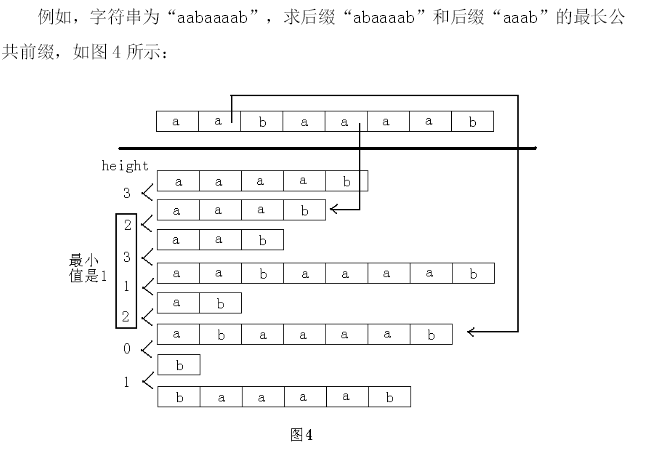
那么现在考虑如何高效求解:
朴素的做法,时间复杂度是O(n^2)的.但不妨利用字符串的性质;定义h[i]=height[rank[i]],意义就是Suffix(i)和它前一名的后缀的LCP;
那么h[i]有一个性质: h[i]>=h[i-1]-1
证明如下:
设Suffix(k)是排在Suffix(i-1)前的后缀,则它们的LCP为h[i-1];那么Suffix(k+1)将排在Suffix(i)前面(这里要求h[i-1]>1,若不满足则显然成立QAQ)并且Suffix(k+1)和Suffix(i)的LCP是h[i-1]-1,所以Suffix(i)和在它前一名的后缀的LCP至少是h[i-1]-1;
按照h[1]~h[n]的顺序去计算,利用这个性质,可以使时间复杂度降到O(n);在实际实现的过程中,没必要记录h数组,只需要按照这个顺序去计算即可
CODE:
char S[maxn]; int SA[maxn],len; int wa[maxn],wb[maxn],ws[maxn],wv[maxn]; inline int cmp(int *r,int a,int b,int l) { return r[a]==r[b]&&r[a+l]==r[b+l];//就像论文所说,由于末尾填了0,所以如果r[a]==r[b](实际是y[a]==y[b]),说明待合并的两个长为j的字符串,前面那个一定不包含末尾0,因而后面这个的起始位置至多在0的位置,不会再靠后了,因而不会产生数组越界。 } inline void DA(char *r,int *sa,int n,int m)//这里的n表示字符串长,m为字符取值范围,即基数排序的限制,如果全字母字符串m可以取128,全数字则为max+1 { int p,*x=wa,*y=wb,*t; //x的本意是存储rank,但这里并不需要彻底存下,只需要能够当做一种比较的时候反应大小的记录 for (int i=0; i<m; i++) ws[i]=0; for (int i=0; i<n; i++) ws[x[i]=r[i]]++; for (int i=1; i<m; i++) ws[i]+=ws[i-1]; for (int i=n-1; i>=0; i--) sa[--ws[x[i]]]=i;//i之所以从n-1开始循环,是为了保证在当字符串中有相等的字符串时,默认靠前的字符串更小一些。 //以上是把各个字符进行基数排序(即H=1) //下面这层循环中p代表rank值不用的字符串的数量,如果p达到n,那么各个字符串的大小关系就已经明了了。 //j代表当前待合并的字符串的长度,每次将两个长度为j的字符串合并成一个长度为2*j的字符串,当然如果包含字符串末尾具体则数值应另当别论,但思想是一样的。 p=1; for (int j=1; p<n; j*=2,m=p) { p=0; for (int i=n-j; i<n; i++) y[p++]=i;//位置在第n-j至n的元素的第二关键字都为0,因此如果按第二关键字排序,必然这些元素都是排在前面的。 for (int i=0; i<n; i++) if (sa[i]>=j) y[p++]=sa[i]-j; //下面一行的第二关键字不为0的部分都是根据上面一行的排序结果得到的,且上一行中只有sa[i]>=j的第sa[i]个字符串(这里以及后面指的“第?个字符串”不是按字典序排名来的,是按照首字符在字符串中的位置来的)的rank才会作为下一行的第sa[i]-j个字符串的第二关键字,而且显然按sa[i]的顺序rank[sa[i]]是递增的,因此完成了对剩余的元素的第二关键字的排序。 //第二关键字基数排序完成后,y[]里存放的是按第二关键字排序的字符串下标 //以上两行是对第二关键字的排序 for (int i=0; i<n; i++) wv[i]=x[y[i]];//这里相当于提取出每个字符串的第一关键字(前面说过了x[]是保存rank值的,也就是字符串的第一关键字),放到wv[]里面是方便后面的使用 for (int i=0; i<m; i++) ws[i]=0; for (int i=0; i<n; i++) ws[wv[i]]++; for (int i=1; i<m; i++) ws[i]+=ws[i-1]; for (int i=n-1; i>=0; i--) sa[--ws[wv[i]]]=y[i]; //上面四行是对第一关键字的基数排序 //下面三行就是计算合并之后的rank值了,而合并之后的rank值应该存在x[]里面,但我们计算的时候又必须用到上一层的rank值,也就是现在x[]里面放的东西,如果我既要从x[]里面拿,又要向x[]里面放,怎么办?当然是先把x[]的东西放到另外一个数组里面,省得乱了。这里就是用交换指针的方式,高效实现了将x[]的东西“复制”到了y[]中。 t=x,x=y,y=t;p=1;x[sa[0]]=0; for (int i=1; i<n; i++) x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;//这里就是用x[]存储计算出的各字符串rank的值了,记得我们前面说过,计算sa[]值的时候如果字符串相同是默认前面的更小的,但这里计算rank的时候必须将相同的字符串看作有相同的rank,要不然p==n之后就不会再循环啦。 } } int rank[maxn],height[maxn]; inline void calheight(char *r,int *sa,int n) { int k=0; for (int i=1; i<=n; i++) rank[sa[i]]=i;//rank和SA互逆运算,所以求得排名 for (int i=0; i<n; height[rank[i++]]=k)//将计算出来的height[rank[i]]的值,也就是k,赋给height[rank[i]]。i是由0循环到n-1,但实际上height[]计算的顺序是由height[rank[0]]计算到height[rank[n-1]]。 {k?k--:0;for (int j=sa[rank[i]-1]; r[i+k]==r[j+k]; k++);} //上一次的计算结果是k,首先判断一下如果k是0的话,那么k就不用动了,从首字符开始看第i个字符串和第j个字符串前面有多少是相同的,如果k不为0,按我们前面证明的,最长公共前缀的长度至少是k-1,于是从首字符后面k-1个字符开始检查起即可。 }