Gym 101466(完整)

题目链接：点击此处

## Problem A

题意：

　　给你n个数，重定义两个数之间的加法不进位，求这些数中两个数相加的最大值和最小值。

题解：

字典树。我们首先将前i-1为放入字典树中，然后在查询第i位时，我们去字典树中查询，对每一位进行寻找，找到满足题意的当前位的最大值和最小值，然后继续更新下一位，最后维护总的最大值和最小值即可。

C++版本一

#include <set>
#include <map>
#include <queue>
#include <stack>
#include <cmath>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long ll;
typedef pair<ll, ll> pll;
typedef pair<ll, int> pli;
typedef pair<int, ll> pil;;
typedef pair<int, int> pii;
typedef unsigned long long ull;

#define lson i<<1
#define rson i<<1|1
#define lowbit(x) x&(-x)
#define bug printf("*********
");
#define debug(x) cout<<"["<<x<<"]" <<endl;
#define FIN freopen("D://code//in.txt", "r", stdin);
#define IO ios::sync_with_stdio(false),cin.tie(0);

const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 1e6 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;

int n;
int le,root;
int arr[20];
ll num, pw[20];

struct node{
    int nxt[10];
    void init(){
        for(int i = 0; i < 10; i++) nxt[i] = -1;
    }
}T[13*maxn];

void insert(ll x){
    int now = root;
    for(int i = 0; i <= 18; i++) {
        arr[i] = x % 10;
        x /= 10;
    }
    for(int i = 18;i >= 0; i--){
        int num = arr[i];
        if(T[now].nxt[num] == -1){
            T[le].init();
            T[now].nxt[num] = le++;
        }
        now = T[now].nxt[num];
    }
}

ll search1(ll x){
    int now = root, mx, idx;
    ll res = 0;
    for(int i = 0; i <= 18; i++) {
        arr[i] = x % 10;
        x /= 10;
    }
    for(int i = 18; i >= 0; i--) {
        mx = -1, idx = -1;
        for(int j = 0; j < 10; j++) {
            if(T[now].nxt[j] != -1 && (j + arr[i]) % 10 > mx) {
                mx = (j + arr[i]) % 10;
                idx = j;
            }
        }
        now = T[now].nxt[idx];
        res = res + mx * pw[i];
    }
    return res;
}

ll search2(ll x){
    int now = root, mx, idx;
    ll res = 0;
    for(int i = 0; i <= 18; i++) {
        arr[i] = x % 10;
        x /= 10;
    }
    for(int i = 18; i >= 0; i--) {
        mx = 11, idx = -1;
        for(int j = 0; j < 10; j++) {
            if(T[now].nxt[j] != -1 && (j + arr[i]) % 10 < mx) {
                mx = (j + arr[i]) % 10;
                idx = j;
            }
        }
        now = T[now].nxt[idx];
        res = res + mx * pw[i];
    }
    return res;
}

int main() {
    le = 1;
    pw[0] = 1;
    for(int i = 1; i <= 18; i++) pw[i] = pw[i-1] * 10;
    T[0].init();
    scanf("%d", &n);
    ll ans1 = INF, ans2 = -1;
    for(int i = 1; i <= n; i++) {
        scanf("%lld", &num);
        if(i > 1) {
            ans1 = min(search2(num), ans1);
            ans2 = max(search1(num), ans2);
        }
        insert(num);
    }
    printf("%lld %lld
", ans1, ans2);
    return 0;
}

View Code

## Problem B

题意

求有根树最多可以有多少个结点。

做法

一个样例来分析：
3
2 1 3
第一个3，说明这棵树有3层（不包括根节点）。
那么，我们是怎么得到这3层的呢？
根节点的子节点的个数是[2, 1, 3]中的一个，
我们假设是2，得到树的第一层。

第一层每个节点的子节点的个数是剩下的[1, 3]中的一个，
我们假设是1，得到树的第二层。

…
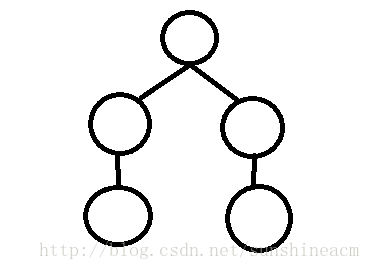
依此类推，直到用完数组中的元素。
（上面的假设得到的就是题目中的图一的树）

那么，我们要怎样才能使得树的结点最多呢？
一个自然的想法，我们让根节点拥有最多的孩子节点，得到第一层，
然后让第一层的每一个节点拥有次多的孩子节点，得到第二层，
依此类推，我们得到的就是拥有最多节点的树。

还是以样例来说明：
3
2 1 3
我们先把数组排序得到：
3 2 1

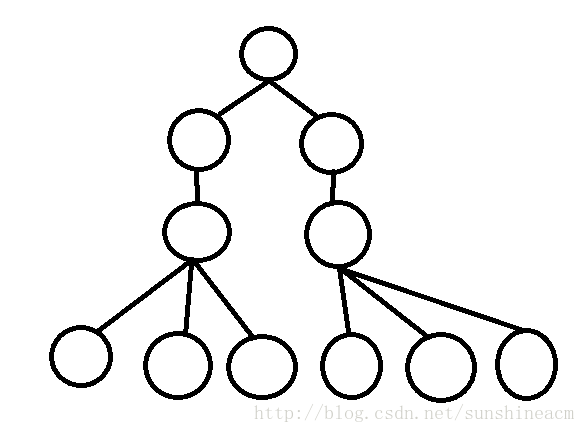
按照上面说的，我们得到下面这样一颗树：

树的节点个数为：

sum = 1 + 3 + 3*2 + 3*2*1。
上式中的各项分别对应于根节点，第一层，第二层，…，的节点个数。

C++版本一

#include <stdio.h>
#include <algorithm>
using namespace std;

bool  // 从大至小排序
cmp(int a, int b) {
    return a > b;
}

int
main() {
    int n, i;
    long long a[35], ans;

    scanf("%d", &n);
    for( i = 0; i < n; i++ ) {
        scanf("%lld", &a[i]);
    }
    sort(a, a + n, cmp);
    for( i = 1; i < n; i++ ) {
        a[i] = a[i] * a[i - 1];  //
    }
    ans = 1;
    for( i = 0; i < n; i++ ) {
        ans += a[i];
    }
    printf("%lld
", ans);

    return 0;
}

View Code

## Problem C

题意

大概意思是地球和其他星球要建立通信，但是发出的信号是一条三维空间的直线，求想要让地球和其他所有星球都建立通信最少需要发射几次信号。

思路

把问题抽象出来就是求三维坐标系下经过地球的那个点以及其他星球所在的点最少能画成几条直线，即判断哪些点是共线的就行。
我的思路是把地球所在的点视为坐标系原点，再把其他星球坐标的符号化为一致，x、y、z坐标分别都除以三者的最大公约数，化为最简。若两个星球坐标化为最简后是一样的，则这两个星球坐标和地球必定共线。

C++版本一

#include <bits/stdc++.h>
using namespace std;

struct Point{
    int x, y ,z;
    Point(){};
    Point(int a, int b ,int c){x = a;y = b;z = c;}
    bool operator == (Point &temp ){
    return x == temp.x && y == temp.y && z == temp.z;
    }
}p[5000 + 10];

//map<Point,int> mp;

int main(){
    int n;
    int tot = 0;
    scanf("%d",&n);
    int ex,ey,ez;
    scanf("%d %d %d",&ex,&ey,&ez);
    for(int i = 2;i <= n ;i ++){
        int x , y ,z;
        scanf("%d %d %d",&x,&y,&z);
        x -= ex ,y -= ey ,z -= ez;
        if(x < 0){
            x = -x;
            y = -y;
            z = -z;
        }else if(x == 0){
            if(y < 0){
                y = -y;
                z = -z;
            }
        }else if(y < 0){
            if(z < 0){
                z = -z;
            }
        }
        int gcd = __gcd(__gcd(abs(x),abs(y)),abs(z));
        x /= gcd,y/=gcd,z/=gcd;
        Point temp;
        temp.x = x , temp.y = y, temp.z = z;
        
        if(tot == 0){
        p[++tot] = (Point){x,y,z};
        }
        else{
            int flag = 0;
            for(int j = 1;j <= tot;j ++ ){
                if((Point){x,y,z} == p[j]) flag ++;
            }
            if(!flag)p[tot++] =(Point){x,y,z};
        }
    }
    printf("%d",tot);
}

View Code

## Problem D

题意

给出一个n，问怎样得到n的。(1 <= n <= 10^9)
我们开始有0块钱，可以通过下面两个方法获得更多的钱：
A：y = 2 * x + 1
B：y = 2 * x + 2

做法

我们逆向考虑一下，题目问我们怎么从0->n，我们从n->0倒过来推。
于是有：
A：x = (y - 1) / 2
B：x = (y - 2) / 2

因为从0->n获得钱的过程中，不会出现钱不是整数的情况，
所以我们从n->0倒过来推，同样如此。
同时，我们发现A和B中，是不会同时可以整除的，也就是说A和B不会同时成立。
因为
A：减1再除以2
B：减2再除以2
（我突然想到了奇偶数，一个数不会既是奇数又是偶数）
所以，我们只需将n整除（通过A/B）至0，同时记录A/B，最后倒过来输出就ok了。

C++版本一

#include <stdio.h>

char ans[1000005];

int
main() {
    int n, i, t = 0;

    scanf("%d", &n);
    while( n!= 0 ) {
        if( (n - 1) % 2 == 0 ) {
            n = (n - 1) / 2;
            ans[t] = 'A';
            t++;
        }
        else if( (n - 2) % 2 == 0 ) {
            n = (n - 2) / 2;
            ans[t] = 'B';
            t++;
        }
    }
    for( i = t - 1; i >= 0; i-- ) {
        printf("%c", ans[i]);
    }
    printf("
");

    return 0;
}

View Code

## Problem E

题意：

模式串的前缀最长且满足母串的字串的数量个数

题解：

二分 + KMP

C++版本一

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 7;
string str1,str2;
const int N = 1000002;
int nexts[N];
//ar S[N], T[N];
/*
* next[] 的含义：x[i-next[i]...i-1]=x[0...next[i]-1] 
* next[i] 为满足 x[i-z...i-1]=x[0...z-1] 的最大 z 值（就是 x 的自身匹配）
*/ 

void getNext(string T,int tlen)
{
    int j, k;
    j = 0; k = -1; nexts[0] = -1;
    while(j < tlen)
        if(k == -1 || T[j] == T[k])
            nexts[++j] = ++k;
        else
            k = nexts[k];

}
/* 
 * kmpNext[i] 的意思:next'[i]=next[next[...[next[i]]]](直到 next'[i]<0 或者 x[next'[i]]!=x[i])
 * 这样的预处理可以快一些 
 */ 
void preKmp(string x[],int m,int kmpNext[]){
    int i,j;
    j=kmpNext[0]=-1;
    i=0;
    while(i<m){
        while(-1!=j && x[i]!=x[j])j=kmpNext[j];
        if(x[++i]==x[++j])kmpNext[i]=kmpNext[j];
        else kmpNext[i]=j;
    }
}
/*
返回x 在 y 中出现的次数，可以重叠
*/
int mynext[maxn];
int KMP_Count(string T,int tlen,string S,int slen)
{
    int ans = 0;
    int i, j = 0;

    if(slen == 1 && tlen == 1)
    {
        if(S[0] == T[0])
            return 1;
        else
            return 0;
    }
    getNext(T,tlen);
    for(i = 0; i < slen; i++)
    {
        while(j > 0 && S[i] != T[j])
            j = nexts[j];
        if(S[i] == T[j])
            j++;
        if(j == tlen)
        {
            ans++;
            j = nexts[j];
        }
    }
    return ans;
}

int main(int argc, char const *argv[])
{
    //cin >> str1 >> str2;
    getline(cin,str1);
    getline(cin,str2);
    int len;scanf("%d",&len);
    int len1 = str1.size();
    int len2 = str2.size();
    int l = 0,r = len2;
    int x = 0;
    while(l < r){
        int mid = (l + r + 1) >> 1;
        //cout << str2 << endl;
        //cout << str2.substr(0,mid) << endl;
        //cout << KMP_Count(str2.substr(0,mid),mid,str1,len1) << endl;
        if(KMP_Count(str2.substr(0,mid),mid,str1,len1) >= len){ 
            l = mid;
            x =max( mid,x);
           
        }
        else r = mid - 1;
    }
    //cout << l << endl;
    if(x) cout << str2.substr(0,x) << endl;
    else cout << "IMPOSSIBLE" << endl;
    return 0;
}

View Code

## Problem F

题意：

给出n行a, b, c, 判断是否每一行a, b, c都可以组成三角形。

题解：

三角形两边之和大于第三边。

C++版本一

#include <stdio.h>

int  // 判断a, b, c是否可以组成三角形
f(int a, int b, int c) {
    if( (a + b > c) && (a + c > b) && (b + c > a) ) {
        return 1;
    }
    return 0;
}

int
main() {
    int n, a, b, c, flag = 1;

    scanf("%d", &n);
    while( n-- ) {
        scanf("%d %d %d", &a, &b, &c);
        if( f(a, b, c) == 0 ) {
            flag = 0;
        }
    }
    if( flag == 0 ) {
        printf("NO
");
    }
    else {
        printf("YES
");
    }

    return 0;
}

View Code

## Problem G

题意：

题解：

C++版本一

//@author lonely_wind
#include <bits/stdc++.h>
using namespace std;

const int maxn = 1e6 + 10;
const int mod = 1e9 + 7;

bool is[maxn];
int prime[maxn],cnt,n;
string s;

void add(int x){
    string t;
    while(x){
        t += x % 10 +'0';
        x/=10;
    }
    reverse(t.begin(),t.end());
    s += t;
}

void upd(int &x){if(x >= mod) x-= mod;}
int dp[(1 << 20) + 5];

int dfs(int now){
    if(dp[now] != -1) return dp[now];
    if(now + 1 == (1 << s.size())) return dp[now] = 1;
    int ret = 0;bool vis[27];
    memset(vis,0,sizeof vis);
    for(int i = 0;i < s.size();i ++){
        if((now & (1 << i)) == 0 && s[i] != '0'){
            if(!vis[s[i] - '0']){
                ret += dfs(now|(1<<i));upd(ret);
                vis[s[i]-'0'] = 1;
            }
            for(int j = 0;j < s.size();j ++){
                if(i == j) continue;
                if(s[i] == '0') continue;
                if((now&(1<<j))!=0)continue;
                int x = (s[i]-'0')*10+s[j]-'0';
                if(x <= 26 && x >= 10 && !vis[x]){
                    if(now == 6 && (now|(1 << i)|(1<<j))==6){
                        int ttt = 1;
                    }
                    ret += dfs(now|(1<<i)|(1<<j));
                    vis[x] = 1;
                }
            }
        }
    }
    return dp[now] = ret;
}

int main(int argc, char const *argv[])
{
    for(int i = 2;i <= 1000000;i ++){
        if(!is[i]){
            prime[++cnt] = i;
            for(int j = i + i;j <= 1000000;j +=i){
                is[j] = 1;
            }
        }
    }
    while(~scanf("%d",&n)){
        s = "";
        for(int i = 1;i <= cnt;i ++){
            while(n%prime[i] == 0){
                add(prime[i]);
                n/=prime[i];
            }
        }
        memset(dp,-1,sizeof dp);
        dfs(0);
        printf("%d
",dp[0]);
    }

    return 0;
}

View Code

## Problem H

题意：

打印字符，输出不同尺寸的’un’。

题解：

观察两个样例，直接做，细心点。

C++版本一

#include <stdio.h>

void f(int n) {
    printf("*");
    for( int i = 1; i <= n - 2; i++ ) {
        printf(" ");
    }
    printf("*");
}

int main() {
    int n, i, j;

    scanf("%d", &n);
    f(n);
    printf(" ");
    for( i = 1; i <= n; i++ ) {
        printf("*");
    }
    printf("
");

    for( i = 1; i <= n - 2; i++ ) {
        f(n);
        printf(" ");
        f(n);
        printf("
");
    }
    for( i = 1; i <= n; i++ ) {
        printf("*");
    }
    printf(" ");
    f(n);
    printf("
");

    return 0;
}

View Code

## Problem I

题意：

n个同学 0--n-1
第i个同学最喜欢的是fi，i是j的朋友，当|i-j| <= k
分两间教室
A 回文
B 迷信，只含4，7

每个人至少一个朋友

题解：

区间内每个人至少一个是朋友且需要在同一间教室
记忆化搜索
dp[fx][fy][x][y][now]
fx：与上一个A孩子的距离
fy: 与上一个B孩子的距离
x:前一个A间教室是否有朋友
y:前一个B间教室是否有朋友
now：当前位置
表示前面考虑好的情况下，当前位置的状态

具体见代码，带注释

C++版本一

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 7;
bitset<maxn> vis[22][22][3][3],dp[22][22][3][3];

ll cnt[maxn],ans[maxn];
int n, k;

bool _1(ll x){
    std::vector<ll> v;
    while(x) v.push_back(x%10),x/=10;
    for(int i = 0;i < v.size(); i++){
        if(v[i] != v[v.size() - 1 - i])
            return false;
    }
    return true;
}

bool _2(ll x){
    while(x){
        if(x%10 != 4 && x%10 !=7) return false;
        x/=10;
    }
    return true;
}

bool dfs(int now,int fx,int fy,int x,int y){
        //当前位置结束却有孩子没有朋友，就不可能
        if(now == n + 1){
            if(x == 0 || y == 0) return false;
            return true;
        }
        //记忆化搜索
        if(vis[fx][fy][x][y][now]){
            return dp[fx][fy][x][y][now];
        }
        bool ret = 0;vis[fx][fy][x][y][now] = 1;
        //当前位置是哪一个教室
        if(ans[now]&1){
            //这个孩子前一个没朋友，且下一个已经超过k+1;
            if(x == 0 && fx >= k + 1){}
            else ret |= dfs(now+1,1,min(k+1,fy+1),fx <= k,y);    
        }
        if(ans[now]&2){
            if(y == 0 && fy >= k + 1){}
            else ret |= dfs(now+1,min(k+1,fx + 1),1,x , fy <= k);
        }
        return dp[fx][fy][x][y][now] = ret;
}

int main(int argc, char const *argv[])
{
    scanf("%d %d",&n,&k);
    for(int i = 1;i <= n ;i ++){
        scanf("%lld",&cnt[i]);
        if(_1(cnt[i])) ans[i] |= 1;
        if(_2(cnt[i])) ans[i] |= 2;
        if(!ans[i]) return !printf("No
");
    }
    //当前位置，与上一个A孩子的距离，与上一个B孩子的距离，前一个A间教室有，前一个B间教室有
    printf("%s
",dfs(1,k+1,k+1,1,1)?"Yes":"No");
    return 0;
}

View Code

## Problem J

题意：

一共n个数字(3<=n<=3e7, 0<=ai<3e7 )，给出前面的m个(3<=m<=min(100, n))，
a[i] = (a[i-m] + a[i-m+1]) % MOD，q个询问(1<=q<=1e4)，询问a[1,n]里的从小到大第bi大。

题解：

桶排序

先按照要求用a[1,m]构造出a[1,n]，然后这里n == 3e7，所以如果采用快速的比较排序算法如归并排序快速排序的时间复杂度是O(nlogn)会超时，因此我们想到可以使用线性排序方法桶排序(或者说计数排序)，建一个数组cnt[3e7+8]，扫一遍a数组，对于每一个ai，cnt[a[i]]++，最后扫一遍cnt数组，就可以把ai排好序了。

C++版本一

#include<bits/stdc++.h>
using namespace std;
const int maxn=3e7+10;
const int mod=3e7;
#define inf 0x3f3f3f3f
int a[maxn],ba[maxn],n,m,q,maxx=-1,minn=inf,tot=0;
int main()
{
    std::ios::sync_with_stdio(false);
    memset(ba,0,sizeof(ba));
    cin>>n>>m>>q;
    for(int i=1;i<=m;i++)
    {
         cin>>a[i];
         ba[a[i]]++;
         maxx=max(maxx,a[i]);
         minn=min(minn,a[i]);
    }
    for(int i=m+1;i<=n;i++)
    {
        a[i]=(a[i-m]+a[i-m+1])%mod;
        ba[a[i]]++;
        maxx=max(maxx,a[i]);
        minn=min(minn,a[i]);
 
    }
    for(int i=minn;i<=maxx;i++)
    {
        for(int j=1;j<=ba[i];j++)
            a[++tot]=i;
 
    }
    while(q--)
    {
        int x;
        cin>>x;
        cout<<a[x]<<endl;
    }
    return 0;
 
 
}

View Code

## Problem K

题意：

　给你一棵有n个节点的树，根节点始终为0，有两种操作：

　　　　1.RAND：查询以u为根节点的子树上的所有节点的权值的乘积x，及x的因数个数。

　　　　2.SEED：将节点u的权值乘以x。

题解：

　　这题一眼线段树，由于是对一棵子树进行处理，因此我们采用常规套路，借助dfs序将子树变成区间。不过因为权值的乘积太大，还要取模，一个数取模后因数个数也会发生变化，所以我们肯定不能用它的权值来进行建树，因而我们可以将思路进行转化，先将它的每个节点的权值进行唯一分解，对指数进行建树。

　　对于最后的答案，第一个乘积x很容易求，用快速幂对2，3，5，7，11，13这六个素数进行处理即可。而第二个答案，我们根据数论知识知道它的结果是∏（1+ci），其中ci为某个因数pi的指数。

C++版本一

#include <bits/stdc++.h>
using namespace std;
typedef long long ll ; 
const int mod = 1e9 + 7;
const int maxn = 1e5 + 7;
int a[maxn];
int prime[6] = {2, 3, 5, 7, 11, 13}, cnts[6], ans[6];
int vis[maxn];
struct node
{
    int to ,nxt;
}e[maxn << 1];

int tot,head[maxn];
int add_edge(int u , int v){
    e[++tot].to = v;
    e[tot].nxt = head[u];
    head[u] = tot;
}
int cnt = 0;
int in[maxn],ou[maxn];
void dfs(int x , int fa){
   in[x] = ++cnt;
    for(int i = head[x]; ~i ; i = e[i].nxt){
        if(fa != e[i].to){
            dfs(e[i].to , x);
        }
    }
    ou[x] = cnt; 
}

struct tree
{
    int l , r;
    int num[6] ;
}t[maxn << 2];

#define lc rt << 1
#define rc rt <<1|1

void push_up(int rt){
    for(int i = 0;i < 6 ; i++){
        t[rt].num[i] = t[lc].num[i] + t[rc].num[i] % mod;
    }
}

void build(int rt , int l ,int r){
    t[rt].l = l,t[rt].r = r;
    for(int i = 0;i < 6 ; i ++){
        t[rt].num[i] = 0;
    }
    if(l == r){
        for(int i = 0; i < 6; i++){
            if(vis[l] % prime[i] == 0){
                while(vis[l] % prime[i] == 0){
                    t[rt].num[i] ++;
                    vis[l] /= prime[i];
                }
            }
        }
        return;
    }
    int mid = (l + r ) >> 1;
    build(lc , l , mid);
    build(rc, mid + 1, r);
    push_up(rt);
}   

void update(int rt,int pos ,int x[]){
    if(t[rt].l == pos && pos == t[rt].r){
        for(int i = 0;i < 6; i++)
        t[rt].num[i] = t[rt].num[i] + x[i] % mod;
    return;
    }
    int mid = (t[rt].l + t[rt].r) >> 1;
    if(pos <= mid){
        update(lc,pos,x);
    }else {
        update(rc,pos , x);
    }
    push_up(rt);
}

int qpow(int x, int n) {
    int res = 1;
    while(n) {
        if(n & 1) res = (ll) res * x % mod;
        x = (ll)x * x % mod;
        n >>= 1;
    }
    return res;
}

void query(int rt ,int l ,int r,int ans[]){
    if(t[rt].l == l && t[rt].r == r){
        for(int i = 0;i < 6; i++){
            ans[i] += t[rt].num[i];
        }
        return;
    }
    int mid = (t[rt].l + t[rt].r) >> 1;
        if(r <= mid){
        query(lc,l,r,ans);
    }else if(l > mid){
        query(rc,l,r,ans);
    }else{
        query(lc,l,mid,ans);
        query(rc,mid + 1,r,ans);
    }
}


int main(int argc, char const *argv[])
{
    int n;
    cin >> n ;
    int x ;
    tot = x = 0;
    memset(head,-1,sizeof head);
    for(int i = 2;i <= n ; i ++){
        int u  , v;
        cin >> u >> v;
        u++, v ++;
        add_edge(u,v);
       // add_edge(v,u);
    }
    dfs(1,-1);
    int m ;
    //cin >> m ;
    for(int i = 1;i <= n ; i++){
        int p;
        cin >> p;
        vis[in[i]] = p;
    }
    build(1,1,n);
    int q;
    cin >> q;
    while(q--){
        string op;
        cin >> op;
        int a = 0, b = 0;
        if(op[0] == 'R'){
            cin >> a;
            a ++;
            for(int i = 0;i < 6 ; i++) ans[i] = 0;
                query(1,in[a],ou[a],ans);
            ll cnt1 = 1,cnt2 = 1;
            for(int i = 0;i < 6;i ++){
                cnt2 = (cnt2 * ((1 + ans[i]) % mod)) % mod;
                cnt1 = (cnt1 * qpow(prime[i], ans[i])) % mod;
            
            }
            cout << cnt1 << " " << cnt2 << endl;
        }else{
            cin >> a >> b;
            a ++;
            for(int i = 0;i < 6; i ++){
                cnts[i] = 0;
                if(b % prime[i] == 0){
                    while(b % prime[i] == 0){
                        cnts[i]++;
                        b /= prime[i];
                    }
                }
            }
            update(1,in[a],cnts);
        }
    }
    return 0;
}

View Code

相关阅读:
C# 实现复杂对象的序列化与反序列化
 C#操纵XML文档（主要是应用程序的配置文件）
滕王阁序——王勃 (注:我至爱的一篇文章)
SmartClient(智能客户端)学习笔记之——Smart Client基本学习资源
 listview按列自动排序的一点补充
 (转)SmartClient(智能客户端)学习笔记之——Microsoft Updater Application Block ApplicationUpdater assembly设计
 用超图实现城市给水的爆管分析
 .net2005中对asp.net中GridView的常用操作
 .net2003中对DataGrid的常用操作
 为DataGrid或者GridView或者DataList最前面增加一排序号
原文地址：https://www.cnblogs.com/DWVictor/p/11342628.html

Gym 101466(完整)

题目链接 ： 点击此处

## Problem A

题意：

题解：

C++版本一

## Problem B

题意

做法

C++版本一

## Problem C

题意

思路

C++版本一

## Problem D

题意

做法

C++版本一

## Problem E

题意：

题解：

C++版本一

## Problem F

题意：

题解：

C++版本一

## Problem G

题意：

题解：

C++版本一

## Problem H

题意：

题解：

C++版本一

## Problem I

题意：

题解：

C++版本一

## Problem J

题意：

题解：

C++版本一

## Problem K

题意：

题解：

C++版本一

题目链接：点击此处